Свойства кристаллических и аморфных твердых тел, страница 7

Материал	Максимальная (техническая) прочность, sВ×10-3		Максимальная (теоретическая) прочность, sтеор×10-3
	МПа	кГ/мм2	МПа	кГ/мм2
«усы»: 1.Al2O3	17	1,73	90	9,2	5
2. SiC	9,2	0,94	200	20,4	22
3. Графит	20	2,04	196	20	9,8
4. Fe	13,4	1,37	60,2	6,14	4,5
SiO2 (нить)	24,6	2,5	90	9,2	4
Макротела 1. NaCl (после полировки водой)	1,3	0.13	7,6	3,88	5,8
2. NaCl (без полировки)	0,005	0,0005	7,6	3,88	1520
3. Сталь, упрочненная	3,2	0,32	40,8	4,16	13
4. Малоуглеродистая сталь	0,3	0,03	40,8	4,16	136
5. SiC	0,411	0,041	87,6	8,94	213
6. Натрийкальциевое стекло	0,1	<0,01	90	9,2	900
7.Si (очищенный)	5,3	0,53	31	3,16	5,8
8. Аморфные метал.	1,5¸3,6	0,15¸0,35	17¸35	1,7¸3,6	10¸11

В табл. 2.1.4 не приведены данные для пористых изделий, макроскопическая прочность которых, особенно на разрыв и изгиб, может быть незначительной или даже ничтожной. Причины, приводящие к резкому, в сотни раз, снижению технической прочности, по сравнению с теоретически возможными значениями, явились предметом раздела физики твердого тела - науки о прочности; успехи, достигнутые ею в последние десятилетия, видны из той же табл. 2.1.4.

Получены материалы в виде "усов", нитевидных кристаллов, волокон и аморфных металлов, для которых это различие уже незначительно, а у специальных сплавов и изделий, подвергнутых упрочняющей обработке не столь велико, как у тех же материалов, но не подвергнутых обработке.

Общепризнанной причиной низкой прочности конструкционных материалов является дефектность их внутренней структуры, причем важную роль играют различные несовершенства – плоские (макродефекты как следствие несовершенства технологии получения, т.е. различные строчечные скопления пор, сегрегации, микротрещины, границы зерен, границы двойников), линейные и точечные дефекты. Но наиболее опасны, конечно, трещины.

2.1.3.2.1. Прочность твердого тела при хрупком и пластическом разрушении

          В 1919 году английский физик Гриффитс высказал предположение о существовании в любом реальном теле множества дефектов – микротрещин, пространственная ориентировка которых настолько разнообразна, что всегда найдется одна или несколько наиболее неблагоприятно расположенных относительно внешней нагрузки и являющихся эффективными концентраторами напряжений (рис.2.1.8). Ему же принадлежит энергетическая схема расчета реальной прочности для хрупких тел на основе представлений теории упругости.

 

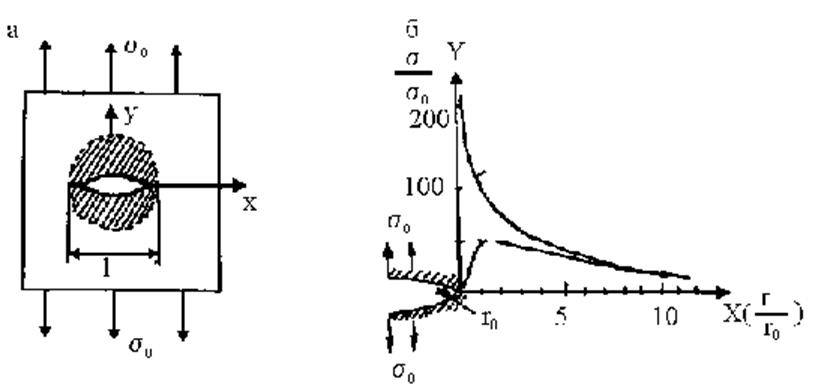
Рис.2.1.8. Распределение напряжений в объеме, прилегающем к вершине хрупкой трещины: а – схема нагружения, б – распределение, рассчитанное на ЭВМ (Гордон и Кук) для трещины с отношением l/r₀=100, где r₀ – радиус в кончике трещины (0,1…0,5 нм). Расстояние Х измерено в плоскости разрушения в единицах r/r₀ от вершины трещины

Тогда в каждой единице упруго деформированного объема будет запасена потенциальная энергия упругой деформации 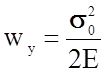. Пусть в образце имелась или возникла сквозная трещина длиной l. В результате образовалась свободная поверхность S = 2ld, что приводит к увеличению потенциальной энергии образца на величину U₁»2ldg, где g = g₀ - поверхностному натяжению при "чисто хрупком" разрушении и  g = g₀ + g_пл при частично пластичном. При вязком разрушении g_пл>> g₀ . Энергия DU₁ смогла выделиться вследствие упругой разгрузки объема образца V»l²d, прилегающего к трещине (заштрихован на рис.2.1,8,а).

Уменьшение потенциальной энергии объема составит

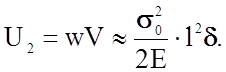
Общее изменение энергии образца DU(l), связанное с появлением в нем трещины длиной l, составит

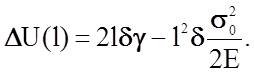                                                        (2.1.30)

Функция DU(l) имеет экстремум (рис. 2.1.9), положение  которого определим, продифференцировав выражение (2.1.30) и приравняв производную к нулю:

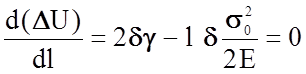
Откуда искомая критическая длина трещины равна

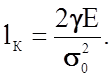                                                                             (2.1.31)

Существуют и другие методы оценки: в частности, используя величину модуля сдвига G и рассмотрев плоское напряженное состояние, можно получить

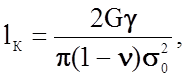                                                                  (2.1.32)

что дает близкую к получаемой из (1.31) величину.

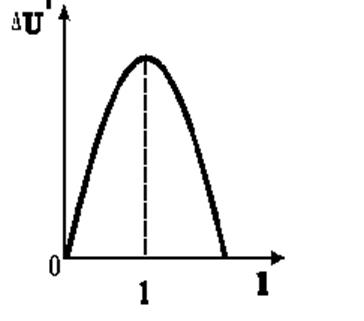Рис. 2.1.9. Зависимость прироста потенциальной энергии образца  от длины существующей в нем трещины

При l³l_К  удлинение трещины за счет упругой энергии, накопленной  деформированным телом становится энергетически выгодным, разрушение идет с ускорением, причем максимальная скорость трещины стремится к теоретическому пределу, равному

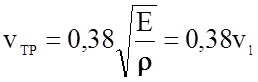,                                                       (2.1.33)

где v_l - скорость продольной волны.

 В стеклах экспериментально наблюдались хрупкие трещины, растущие со скоростями от 700 до 1700 м/с, а в кварцевом стекле - и до 2200 м/с. Такого же порядка скорости разрушения характерны и для сталей, особенно велики скорости трещин в закаленных сталях и других упрочненных материалах.

Кажущееся противоречие об уменьшении критического размера трещины при росте прочности материала (см. данные для  NaCl и стекла в табл.2.1.5) легко устраняется, если принять во внимание, что в  окрестности вершины трещины наблюдается концентрация напряжений (рис. 2.1.8,6).

Напряжение в вершине трещины s_к  зависит от номинального напряжения s₀ в объеме, длины l трещины и радиуса r₀  в ее вершине:

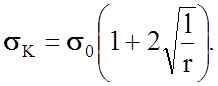                                                              (2.1.34)