В уравнениях (2.1.16) и (2.1.17) G - модуль сдвига, ГПа, d - расстояние между сдвигаемыми атомными плоскостями, обычно плоскостями наиболее плотной упаковки.
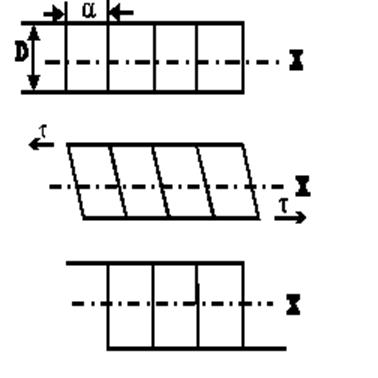 Рис. 2.1.4. Гомогенный сдвиг атомных цепочек друг
относительно друга под действием касательных напряжений. Штрих - пунктирной
линией показано положение плоскости скольжения.
Рис. 2.1.4. Гомогенный сдвиг атомных цепочек друг
относительно друга под действием касательных напряжений. Штрих - пунктирной
линией показано положение плоскости скольжения.
Подставляя найденное значение А в уравнение (2.1.14), получим напряжение t сопротивления деформации гомогенного сдвига
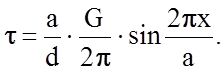 (2.1.18)
(2.1.18)
Максимальное,
критическое значение величины t = tk
соответствует 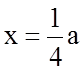 (рис. 2.1.5)
(рис. 2.1.5)
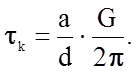 (2.1.19)
(2.1.19)
Из этого соотношения видно, что величина критического напряжения сдвигообразования зависит от соотношения параметров элементарной ячейки a и d, что отражает анизотропию кристаллов, различие в величинах сил межатомного взаимодействия в различных направлениях решетки.
Применительно к наиболее симметричной кубической решетке и аморфному телу с приблизительно равноосной симметрией внутренних межатомных сил можно принять a=d и оценить максимальную
(теоретическую) величину сопротивления твердого тела пластической
деформации путем гомогенного сдвигообразования сразу по всей плоскости скольжения:
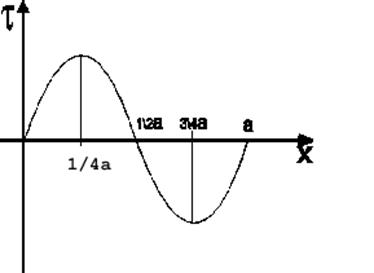
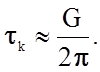
Рис. 2.1.5. Распределение в решетке касательных напряжений t, препятствующих сдвигу
Более строгий и точный расчет дает сравнимую по порядку, но почти в 5 раз меньшую величину
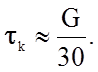 (2.1.20)
(2.1.20)
В табл.2.1.2 приведены теоретические и экспериментальные данные о пластичности некоторых чистых веществ. Вообще точными измерениями показано, что даже при малых напряжениях у многих кристаллических тел отмечаются явления микропластичности. Например, для железа, очищенного зонной плавкой, предел упругости достигает лишь 28 МПа (~2,8 кГ/мм2) и даже менее. Но если речь ведется о гомогенном сдвиге, то это означает участие в деформации значительного объема материала и, следовательно, о макроскопической текучести. Это явление более исследовано и более свойственно металлам. Стекло проявляет текучесть лишь при повышенных температурах, большинство неметаллических кристаллов также малопластичны. tk теоретическое в табл. 2.1.2 определялось по формуле (2.1.20).
Анализируя данные табл.2.1.2, следует признать, что протекание деформации путем гомогенного (или одновременного) сдвига - маловероятный способ деформации, более характерный для аморфных и высокоупрочненных материалов. Но для этих материалов чаще наступает разрушение хрупким разрывом, чем разрушение срезом вследствие большой пластической деформации.
Многочисленные экспериментальные исследования показали, что процессы деформации и текучести являются сложными многопараметровыми явлениями. Предел текучести, например, меди может увеличиться в 2...3 раза вследствие введения примесей в десятые доли процента, предварительного наклепа или, наоборот, отжига. Для всех поликристаллических тел отмечается зависимость Петча макроскопического предела текучести sТ от диаметра зерна:
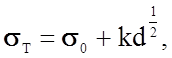 (2.1.21)
(2.1.21)
где s0, k - константы материала и способа нагружения. С уменьшением размера зерна пластические свойства снижаются, а прочность увеличивается
Таблица 2.1.2
Теоретические и экспериментальные данные о пластичности
поликристаллических веществ
|
Материал |
Тип решетки |
tk, МПа эксперим. |
tk, МПа теоретич. |
|
G, ГПа |
|
Cu |
ГЦК |
1 |
1540 |
1540 |
46,2 |
|
a-Fe |
ОЦК |
28 |
2300 |
82 |
69 |
|
LiF |
ГЦК |
3,8 |
1700 |
447 |
51 |
|
Аморфные металлы |
- |
~103 |
(1…2)103 |
1…2 |
30-65 |
|
Упрочн. металлы, легир. стали |
- |
2,5×103 |
17×103 |
~7 |
500 |
Из данных табл. 2.1.2
следует, что отношение 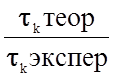 различается на
порядок для решеток разного типа и колеблется для разных веществ от ~102
до ~2×103.
различается на
порядок для решеток разного типа и колеблется для разных веществ от ~102
до ~2×103.
Причина столь разительного
отличия сопротивления реальных тел пластической деформации в сравнении с
предельными теоретическими свойствами заключается в наличии в телах подвижных
микродефектов. Общепризнанным фактом является определяющее влияние на
пластические свойства движения дислокаций. Вообще в скольжении могут
участвовать не все плоскости кристалла, а лишь плотноупакованные. Для активации
движения дислокаций в разных плоскостях кристалла требуются различные, менее чем
в 10 раз различающиеся, механические напряжения. Но порядок величины
напряжений, достаточных для начала скольжения дислокаций (напряжения Пайерлса)
можно оценить. Так, для движения краевых дислокаций с вектором Бюргерса ![]() достаточны сдвиговые напряжения t, определяемые формулой (см. ч.1)
достаточны сдвиговые напряжения t, определяемые формулой (см. ч.1)
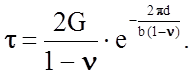
Примем n = 0,3; d = b » 10-9м, тогда t » (3,6×104)G, что составит для материалов, приведенных в табл.2.1.2: Cu - 16,6 МПа; a-Fe - 24,8 МПа, LiF- 18,4 МПа; легированные стали и сплавы ~ 180 МПа.
Эти результаты существенно ближе к экспериментальным данным, чем к теоретическим. Более точные расчеты величины напряжений, достаточных для движения самых подвижных элементов линий дислокации - двойных перегибов - дают еще лучшее совпадение с экспериментальными результатами.
Таким образом, можно считать установленным, что деформация скольжением в аморфных и высокоупрочненных материалах может реализоваться путем гомогенного сдвига элементов тела, а в моно- и поликристаллических телах происходит движение дислокаций различного типа. Выход каждой дислокации на поверхность представляет элементарный сдвиг на один параметр решетки (рис. 2.1.6). Механизм подобен движению складки ковра и требует существенно меньших (в 100...1000 раз) напряжений. Действительно, атому А уже при малом смещении энергетически выгоднее установить связь с атомом 2, чем удерживать связь с атомом 1.
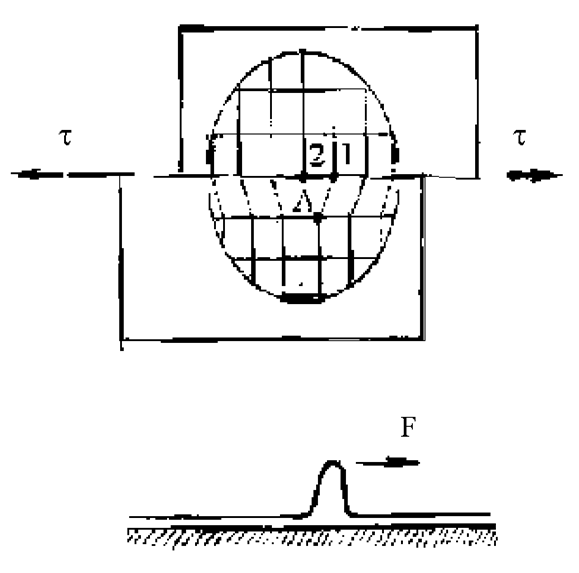 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.