3. Экспериментально показано, что, в принципе, возможно осуществление торможения трещины сильным магнитным полем в проводящих материалах и сильным электрическим - в диэлектриках. Очень эффективно хрупкая трещина тормозится термическими полями.
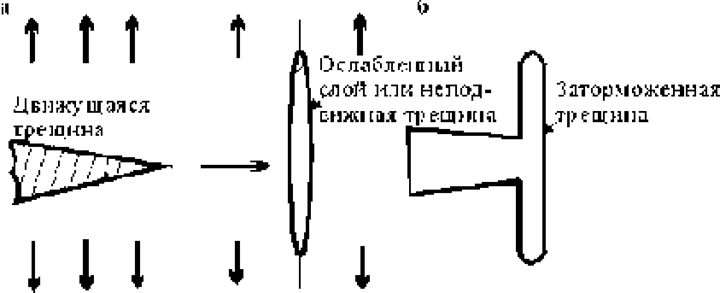
4. Трещина может самопроизвольно или принудительно тормозиться вследствие ветвления с уходом траектории из области максимальных механических напряжений.
Таким образом, вполне объективно можно говорить о возможности заметной, а порой и значительной продолжительности эксплуатации изделий и конструкций из гетерогенных по структуре или физико-механическим свойствам материалов.
Округлая конфигурация пор, лежащих в плоскости движения трещин, чисто "геометрическим" путем притупляет вершину даже полностью хрупкой трещины и тем самым противодействует ее ускорению.
Прочность дефектных тел в последнее время выделяется в отдельную отрасль обширной науки механики разрушения, обзор исследований и некоторые интересные результаты в этой отрасли можно найти в книге Витвицкого П.М. и Полина С.Ю., где используется вероятностный подход к расчету хрупкой прочности.
Ограничимся феноменологическим рассмотрением концентрации поврежденности структуры и распространения трещин (по Л.М.Качанову и Ю.Н.Работнову). Пусть образец находится в поле длительно действующих напряжений, при этом в нем происходит так называемое явление ползучести, медленное накопление дефектов в объеме. Например, у высокопрочных бетонов при одноосной нагрузке может происходить накопление деформации до e = 200×10-5 при сжатии и только до 15×10-5 при растяжении, затем появляются быстро увеличивающиеся микротрещины. В неоднородном поле напряжений деформации сжатия могут достигать до e = 10-2.
 |
В целом деформация сопровождается постепенным ухудшением структуры материала. Сначала распределенные случайно малые пустоты объединяются в микротрещины докритического размера. В результате воспринимающая нагрузку площадь сечения изделия уменьшается. В таком состоянии обычное определение s = F/S0 теряет свой смысл, поскольку величина S0 не поддается определению ни геометрическими, ни (на этой стадии) физическими методами. Истинное напряжение равно
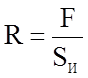. (2.1.36)
Отметим, что подобным образом определяется "истинный предел прочности", где в качестве SИ берут площадь поперечного сечения образцов в момент разрушения. Л.М.Качанов и Ю.Н.Работнов ввели параметр повреждаемости
W = 1 - Y, (2.1.37)
где
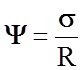(2.1.38)
- безразмерная характеристика.
Параметр w изменяется от w = 0 в совершенно неповрежденном материале до w = 1 в полностью поврежденном, когда его несущая способность равна 0. Из анализа процесса разрушения был постулирован закон роста поврежденности
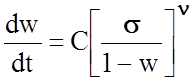, (2.1.39)
где С и n - константы материала, и выведено выражение для долговечности при чисто хрупком разрушении под действием напряжений s:
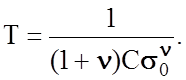(2.1.40)
Если напряжения действуют ступенями s01 , s02 ,..., последовательно, в течение интервалов времени t1, t2,..., то получится нормированное условие разрушения при ползучести:
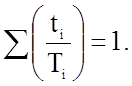(2.1.41)
Рассмотренный комплекс представлений носит название "механики непрерывной поврежденности", и ее следует отличать от обычной механики разрушения. Важным результатом "механики непрерывной повреждаемости" является уравнение
, (2.1.42)
согласно которому истинное напряжение растяжения в повреждаемом материале зависит как от номинальных напряжений s0, так и а д д и -т и в н ы х эффектов деформирования e и поврежденности w . С ростом поврежденности w истинные напряжения быстро, экспоненциально, увеличиваются.
В технологии горно-металлургического производства, производства строительных материалов, огнеупоров и технической керамики важное место занимает процесс измельчения неорганического природного сырья и некоторых искусственно полученных материалов - руды, клинкера, гипса, угля, промежуточных продуктов спекания, отходов других отраслей народного хозяйства. Различают две стадии измельчения: дробление и помол, в свою очередь, по степени крупности каждая стадия подразделяется на три этапа обработки - грубое, среднее и тонкое (мелкое) дробление или измельчение.
Получение все новых керамических материалов более высокого качества требует все более тщательной подготовки порошкового сырья путем его гомогенизации при перемешивании. Активность в физико-химических процессах веществ также совершенно определенно увеличивается по мере вырастания их дисперсности, но, оказывается, зависит не только от величины удельной поверхности. Поэтому интенсивные исследования процесса измельчения и свойств высокодисперсных материалов ведутся во всех развитых странах.
Установлено, что измельчение представляет собой достаточно сложный процесс комбинированного механико-физико-химического воздействия, при котором наряду с диспергированием под действием механических напряжений происходят значительные изменения кристаллической структуры поверхностных слоев частиц и ее аморфизация. Важную, а порой определяющую роль в этом процессе может играть и окружающая среда - газы и влага атмосферы, вода и ПАВ, специально добавляемые в измельчаемую среду.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.