Свойства кристаллических и аморфных твердых тел, страница 2

ПРИМЕЧАНИЕ:  Автор приносит свои извинения за неполноту таблицы, что связано как с неопреденностью некоторых характеристик, так и отсутствием соответствующих открытых публикаций вследствие, видимо, стратегического значения новых материалов.

2.1.1. Упругость и пластичность твердых тел

Внутри тела, подверженного действию внешних сил, возникает напряженное  состояние, количественно характеризуемое механическими напряжениями. Механические напряжения численно равны силе, действующей на единицу площади сечения. Если сечение перпендикулярно силе, то речь идет о нормальных напряжениях s = F/S. Различают нормальные s_n и касательные (скалывающие) (Рис.2.1.1,а) напряжения (часто обозначают t).

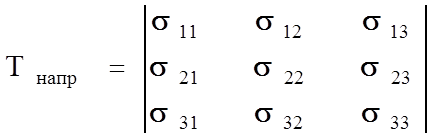Если в образце выделить кубический объем (Рис.2.1.1,б) с осями –x, y, z, обозначенными 1,2,3 соответственно, то можно выделить 9 компонентов механических напряжений, возникающих под действием силы. Напряжения s₁₁, s₂₂, s₃₃ нормальные (растягивающие или сжимающие); s₂₁(t₂₁), s₁₂(t₁₂), s₂₃(t₂₃ ) и т.д. - касательные (сдвиговые или скалывающие) напряжения. Итак, напряженное состояние в точке характеризуется девятью величинами s_ij , которые являются компонентами тензора механических напряжений - тензора второго ранга:

                                                             (2.1.1)

Под действием внешних сил происходит изменение межатомных расстояний, проявляющееся макроскопически как деформация материала, после значительных деформаций - разрушение. На характер распределения напряжений и деформации существенно влияет напряженное состояние материала, степень стесненности деформации.

Д е ф о р м а ц и я - изменение формы твердого тела или его объема без изменения массы под действием внешней силы. Виды деформации - растяжение, сжатие, сдвиг, кручение, изгиб. Последние два сводятся к деформациям растяжения (сжатия) и сдвигу, которые называются  о с н о в н ы м и. Аналогично напряжениям деформированное состояние тела в данной его точке описывается тензором деформаций, тоже второго ранга

В формуле (2.1.2) e_ij - относительная деформация. На рис.2.1.2, а,б представлены основные виды деформации под действием касательных и нормальных напряжений. Относительное удлинение e₁₁ = e_xx определяют как

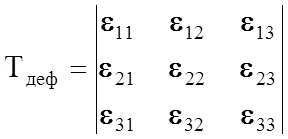
                                                                                                                                                                                                                                          (2.1.2)                    

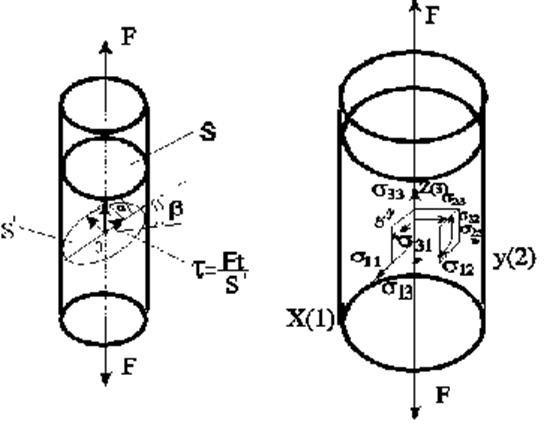
Рис. 2.1.1. Механические напряжения, действующие на образец (а) и грани выделенного куба (б)

т.е. отношение приращения длины к начальной длине образца (рис.2.1.2,б). Относительный сдвиг g = e₁₂ представляет собой тангенс угла a  сдвига (рис.2.1.2,а)

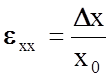                              (2.1.3)

 Качественно и количественно различаются   у п р у г а я     и  п л а с т и ч е с к а я   д е ф о р м а ц и и. Тело, деформированное упруго, после снятия внешней нагрузки полностью восстанавливает свою исходную форму, положение всех атомов тела и расстояния между ними восстанавливаются. Деформация является пластической, если после снятия нагрузки в теле наблюдаются необратимые остаточные изменения. О "чисто упругой деформации" можно говорить лишь условно, до точности, доступной измерительной технике. Как правило, говорят лишь об условном пределе. Чаще всего деформацию считают упругой, если остаточные изменения не превышают 0,2% (e = 0,002), иногда принимают более грубый предел в 1%, но иногда возникает необходимость повысить точность до e = 0,001%, однако это связано со значительными методическими трудностями.

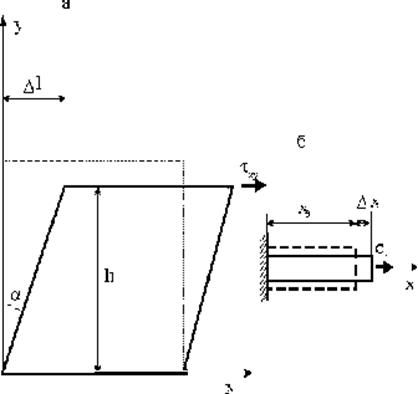Рис.2.1.2. Развитие деформаций в твердом теле под действием касательных t (а) и нормальных s (б) напряжений

1.1.1. Механические напряжения и деформации

Из экспериментов известно, что в пределах упругости выполняется закон Гука о пропорциональности деформаций механическим напряжениям. Получим его из фундаментальных представлений о силе и энергии взаимодействия атомов внутри тела.

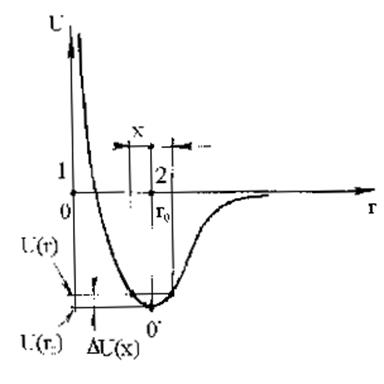
Рис.2.1.3. Потенциальная энергия двух взаимодействующих частиц 1 и 2

На рис. 2.1.3 условно изображена зависимость потенциальной энергии U(r)  взаимодействия частиц 1 и 2 от расстояния г  между ними. Отклонение частицы 2 от положения равновесия r₀  (растяжение или сжатие модели) на величину x - приводит к увеличению потенциальной энергии  DU(x) = U(r₀) – U(r). Полагая это изменение небольшим, разложим DU(x) в ряд Тейлора по степеням x: в окрестности положения равновесия O’:

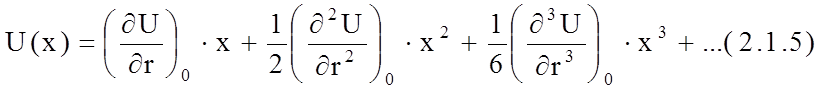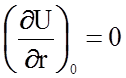Учтем, что в точке O’  производная  и запишем, ограничиваясь записанными членами разложения

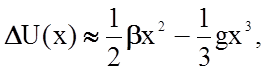                                                         (2.1.6)

где b - коэффициент жесткости межатомной связи, зависящий от валентности, типа решетки, типа связи, a g – коэффициент ангармоничности, выражающий асимметрию потенциальной ямы.

Для описания деформационного поведения твердого тела в пределах упругости достаточно ограничиться первым членом уравнения (2.1.6)

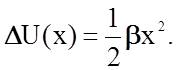                                                                      (2.1.7)

При изменении расстояния между частицами 1 и 2 на величину x между ними возникает сила (f)

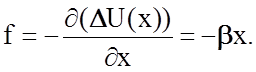                                                          (2.1.8)

Эта формула и выражает закон Гука применительно к элементарному акту взаимодействия пары атомов. Знак минус означает направленность внутренней возвращающей силы к положению равновесия, в которое и вернется система, если внешнее воздействие устранить. Для макроскопических тел элементарный закон Гука записывают в форме

s = Е×e,                                                                                    (2.1.9)