Свойства кристаллических и аморфных твердых тел, страница 6

Если подставить в формулу (2.1.22) численные значения, то получим величину (s_теор » 3,39×10¹¹ Па (3390 кГ/мм²). Из табл. 1.2 для  NaCl модуль упругости Е = 38 ГПа, таким образом, теоретическая прочность кристалла NaCl s_теор » 0,9 Е. Оценка для других кристаллических веществ из табл.1.2 дает  s_теор ~ (0,1…1) E, для силикатного стекла 0,2 Е, т.е. теоретическая прочность достигает .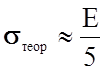

б) по Поляни

При теоретическом изучении физики разрушения твердых тел широко применяется энергетический подход, в основе которого лежат представления о расходе запаса упругой потенциальной энергии деформации на работу создания новых поверхностей, вскрываемых трещинами внутри объема тела.

Пусть к стержню единичного поперечного сечения (1 м²  или 1 см²) приложено растягивающее напряжение s (рис. 2.1.7,6). Под действием этого напряжения соответствующие межатомные расстояния и расстояния между атомными плоскостями увеличиваются. Предположим, что для осуществления разрыва необходимо межатомные расстояния увеличить вдвое, на столько же - величину межплоскостных расстояний, то есть, если исходный параметр решетки вдоль линии действия силы был равен “a”, то разрушение произойдет при таком уровне напряжений s_теор, при котором произойдет смещение атомных плоскостей в зоне разрыва на величину  “а”.

Примем работу, совершенную разрушающими силами, равной s_теор×а. Эта работа переходит в свободную энергию двух вновь образованных поверхностей 2g (g - поверхностная энергия или поверхностное натяжение твердого тела), таким образом,

s_теор×а = 2g,  откуда

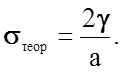                                                                              (2.1.23)

Используя формулу (2.1.23), оценим предельную прочность для некоторых материалов.

 Полученные значения теоретической прочности очень высоки. В табл.2.1.3 использованы данные о поверхностной энергии, не включающей работу пластической деформации, т.е. данные для предельно

хрупкого разрушения, наблюдаемого при Т£ 77 К - температуре кипения жидкого азота.

С повышением температуры величина g возрастает. По предложению Орована, принято считать поверхностную энергию, определяемую из результатов опытов по разрушению, в виде суммы

g = g₀ + g_пл,                                                                           (2.1.24)

g₀ - поверхностное натяжение вещества, g_пл (g_S)  - удельная работа пластической деформации материала по берегам трещины. Даже для сравнительно хрупких материалов величина g_пл может значительно (в 5...15 раз) превосходить поверхностное натяжение, соответственно возрастет и значение теоретической прочности.                                                                                     

  Таблица 2.1.3

Оценка предельной прочности некоторых монокристаллов

по Поляни

Монокристалл (в скобках – плоскость скола)	Поверхностная энергия g, мДж/м2	Параметр решетки, нм	sтеор, МПа	sтеор, кГ/мм2	Модуль упругости Е, ГПа
NaCl (100)	300	0,287	2090	213	43,7	0,05
MgO (100)	1310	0,210	12476	1273	245	0,05
Ge (111)	968	0,566	3420	349	155	0,02
C(алмаз) (111)	3500	0,357	19608	2000	1200	0,016
a - Fe (100)	1440	0,316	9114	930	132	0,07

в) По Оровану и Поляни

Рассмотрим разрушение идеального твердого тела, безотносительно к типу его внутренней структуры и типу межатомных сил (ионные, ковалентные, металлические, кристалл или аморфное тело). В соответствии с фундаментальными представлениями (ч.1, рис. 1.1.3), для разрушения структуры отрывом необходимо преодолеть силы межатомного притяжения. Область их действия заштрихована на рис.2.1,7,в.

Эти силы изменяются с расстоянием сначала, при малых смещениях, почти линейно, и здесь выполняется закон Гука, затем - более сложным образом. Пусть в пределах области их эффективного влияния они изменяются по синусоидальному закону. Переходя от сил к механическим напряжениям, можно записать

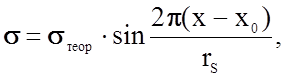                                                    (2.1.25)

где s_теор - максимальная (теоретическая) прочность, определяемая максимальной силой, необходимой для разрыва межатомных связей;

(х – х₀) - смещение относительно положения х₀, r_S - радиус действия сил притяжения.

Разрыв связей происходит на линейной части характеристики f(r), по крайней мере, прирост расстояния (x – x₀) < x₀, макроскопически хрупкое разрушение наступает до достижения предела упругости материала. Поэтому величину смещений атомов можно считать малой и положить

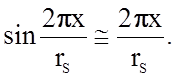
Тогда уравнение (2.1.23) приобретает вид

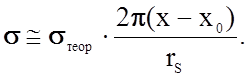                                                         (2.1.26)

В соответствии с законом Гука, в данном случае

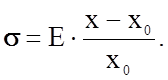                                                                     (2.1.27)

Приравнивая (1.23) и (1.27), получаем

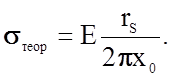                                                                    (2.1.28)

Полагая  приближению  r_s = x₀ = a - параметру решетки, находим

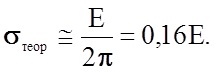                                                              (2.1.29)

Таким образом, теоретические оценки предельной прочности твердых тел дают огромную величину в пределах (0,02... 0,9)Е = 10⁹¸ 10¹⁰ Па, разительно отличающуюся от реальных данных для макроскопических твердых тел.

2.1.3.2. Техническая (реальная) прочность твердых тел

В технике используется реальная или техническая прочность s_p (s_и, s_сж), которая для массивных материалов весьма далека от теоретической даже у высококачественных материалов.

В табл. 2.1.4 приведены значения экспериментально найденной прочности некоторых материалов и сравнительные данные о предельной их прочности, оцененной как 0,2Е.

 Таблица 2.1.4

Сравнительные данные максимальной технической и предельной теоретической прочности некоторых материалов на разрыв