Изучение понятия и свойств непрерывной и дискретной свертки. Вариант 1

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

Дисциплина  «Теория  и  обработка  сигналов»

ЛАБОРАТОРНАЯ  РАБОТА  № 5

НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ СВЕРТКИ

Группа:   АТ-33        

Вариант: 1                                                                                                Преподаватель:

Студент: Шадрина А.В.                                                                           доц. Щетинин Ю.И.

2005

Цель работы:Изучение понятия и свойств непрерывной и дискретной свертки, приобретение практических навыков вычисления свертки  в среде Matlab.

Выполнение работы:

1.         Непрерывная и дискретная  свертки.

Непрерывной свёрткой двух функций   и    называется интеграл вида .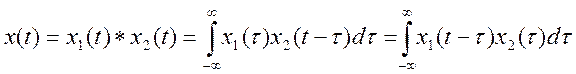

Дискретной свёрткой последовательностей  и  называется последовательность   вида .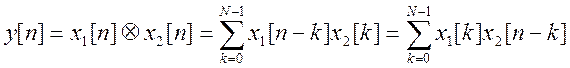

2.         Приближенное вычисление непрерывной свертки сигнала прямоугольной формы и экспоненциального сигнала.

Численное вычисление непрерывной свертки может быть аппроксимировано конечной суммой вида 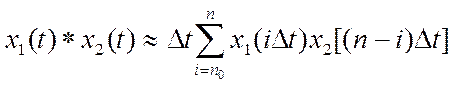, где  - интервал (шаг) дискретизации.

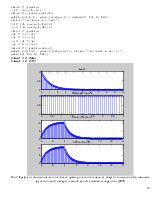
Matlab script(labrab52.m)

T = 0.1;                       %шаг дискретизации  

a = 5;                         %коэффициент при степени экспоненты

i = 0:50;

x1 = exp(-a*i*T);               %сигнал x1

x2 = rectpuls(i-10,20);         %сигнал x2

n1 = length(x1);

n2 = length(x2);

subplot(411),  plot(i*T,x1), title('x1'),grid

subplot(412),  plot(i*T,x2), title('x2'),grid

k1 = 1:n1+n2-1;

%вычисление  свертки

for  n = 1:n1+n2-1,

   y(n) = 0;

   for k = max(1,n+1-n1):min(n,n2),

      y(n) = y(n)+sum(x1(n+1-k)*x2(k));

   end

y(n) = y(n)*T;  

end

%графиксверткисигналов

subplot(413), plot(k1*T,y),title(' Convolution: x1*x2'),grid

%вычисление свертки с помощью функции conv()

subplot(414), plot(k1*T,T*conv(x1,x2))

title(' Convolution (conv):x1*x2'),grid

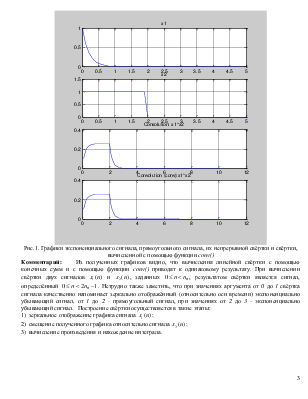
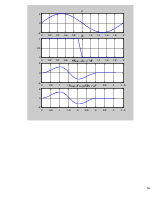
Рис.1. Графики экспоненциального сигнала, прямоугольного сигнала, их непрерывной свёртки и свёртки, вычисленной с помощью функции conv()

Комментарий:          Из полученных графиков видно, что вычисления линейной свёртки с помощью конечных сумм и с помощью функции conv() приводят к одинаковому результату. При вычислении свёртки двух сигналов  и , заданных , результатом свёртки является сигнал, определённый . Нетрудно также заметить, что при значениях аргумента от 0 до 1 свёртка сигнала качественно напоминает зеркально отображённый (относительно оси времени) экспоненциально убывающий сигнал, от 1 до 2 - прямоугольный сигнал, при значениях от 2 до 3 - экспоненциально убывающий сигнал.   Построение свёртки осуществляется в такие этапы:

1)  зеркальное отображение графика сигнала ;

2)  смещение полученного графика относительно сигнала ;

3)  вычисление произведения и нахождение интеграла.

3.         Вычисление непрерывной свертки сигнала треугольной формы и прямоугольной формы.

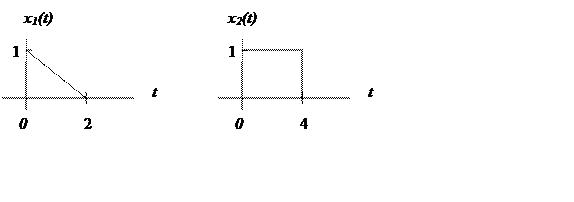
Рис.2. Графики треугольного и прямоугольного сигналов

Matlab script(labrab53.m)

T = 0.1;                       %шаг дискретизации  

i = 0:50;

x1 = tripuls(i-10,20,-1);       %сигнал x1

x2 = rectpuls(i-20,40);         %сигнал x2

n1 = length(x1);

n2 = length(x2);

subplot(411),  plot(i*T,x1), title('x1'),grid

subplot(412),  plot(i*T,x2), title('x2'),grid

k1 = 1:n1+n2-1;

%вычисление  свертки

for  n = 1:n1+n2-1,

   y(n) = 0;

   for k = max(1,n+1-n1):min(n,n2),

      y(n) = y(n)+sum(x1(n+1-k)*x2(k));

   end

y(n) = y(n)*T;  

end

%графиксверткисигналов

subplot(413), plot(k1*T,y),title(' Convolution: x1*x2'),grid

%вычисление свертки с помощью функции conv()

subplot(414), plot(k1*T,T*conv(x1,x2))

title(' Convolution (conv):x1*x2'),grid

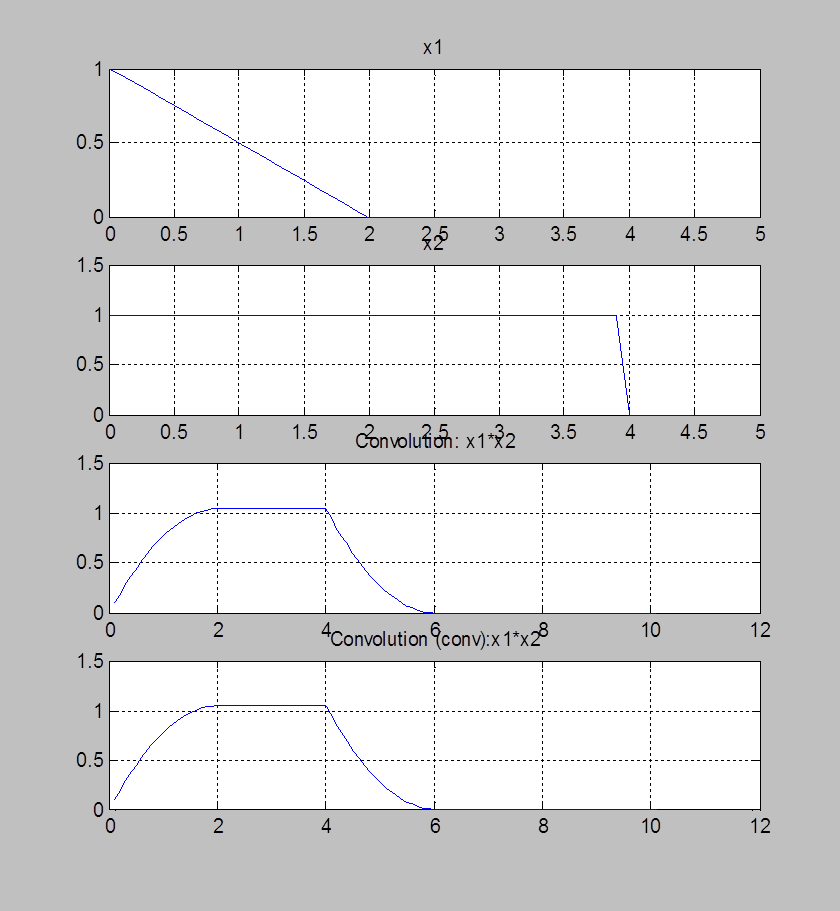
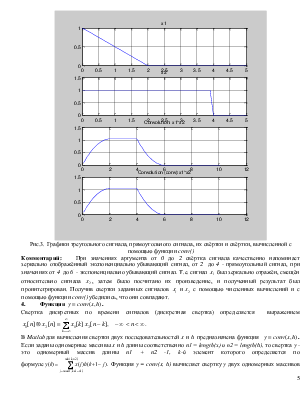
Рис.3. Графики треугольного сигнала, прямоугольного сигнала, их свёртки и свёртки, вычисленной с помощью функции conv()

Комментарий:          При значениях аргумента от 0 до 2 свёртка сигнала качественно напоминает зеркально отображённый экспоненциально убывающий сигнал, от 2  до 4 - прямоугольный сигнал, при значениях от 4  до 6  - экспоненциально убывающий сигнал. Т.е. сигнал  был зеркально отражён, смещён относительно сигнала , затем было посчитано их произведение, и полученный результат был проинтегрирован. Получив свертки заданных сигналов  и с помощью численных вычислений и с помощью функции conv() убедились, что они совпадают.

4.         Функция .

Свертка дискретных по времени сигналов (дискретная свертка) определяется  выражением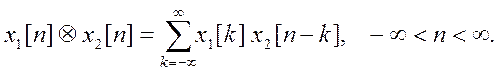
В Matlab для вычисления свертки двух последовательностей x и h  предназначена функция  . Если заданы одномерные массивы x и h длины соответственно n1 = length(x) и n2 = length(h), то свертка y - это одномерный массив длины n1 + n2 -1, k-й элемент которого определяется по формуле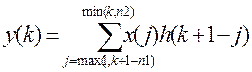. Функция y = conv(x, h) вычисляет свертку y двух одномерных массивов x и h. Рассматривая эти массивы как выборки из двух сигналов, можно сформулировать теорему свертки в следующей форме: если X = fft([x zeros(1, length(h)-1]) и H = fft([h zeros(1, length(x) - 1]) - согласованные по размерам преобразования Фурье сигналов x и h, то справедливо соотношение conv(x, h) = ifft(X.*H). Иначе говоря, свертка двух сигналов эквивалентна умножению преобразований Фурье этих сигналов.

5.         Генерирование прямоугольной последовательности импульсов (прямоугольной волны) длиной L отсчётов и периодом T отсчётов с помощью функции sqgen(L,T).

square(t,duty) – функция генерирует последовательность прямоугольных импульсов с периодом 2π для последовательности отсчётов, определяемой в векторе t, параметр duty задает продолжительность положительной полуволны в процентах от периода.

Matlab function(sqgen.m)

function X = sqgen(L,T)

t = 0:1:L-1;

f = 1/T;

X = square(2*pi*f*t);

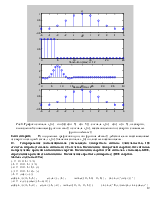
6.         Генерирование единичного импульса  delta1=[1]. Свёртка delta1  и sqgen(50, 10).

Matlab script(labrab54.m)

T = 1;                    %шаг дискретизации

i = 0:1:49;

x1 = 1;                   %сигнал delta1=[1]

x2 = sqgen(50,10);        %сигнал  x2

n1 = length(x1);

n2 = length(x2);

subplot(411),  stem(0,x1), title('delta1=[1]')

subplot(412),  stem(i*T,x2),  title('sqgen(50, 10)')

k1 = 1:n1+n2-1;

%вычисление  свертки

for  n = 1:n1+n2-1,

   y(n) = 0;

   for k = max(1,n+1-n1):min(n,n2),

      y(n) = y(n)+sum(x1(n+1-k)*x2(k));

   end