y(n) = y(n)*T;
end
%графиксверткисигналов
subplot(413), stem(k1*T,y),title(' Convolution: x1*x2')
%вычисление свертки с помощью функции conv()
subplot(414), stem(k1*T,T*conv(x1,x2)), title('Convolution (conv):x1*x2')
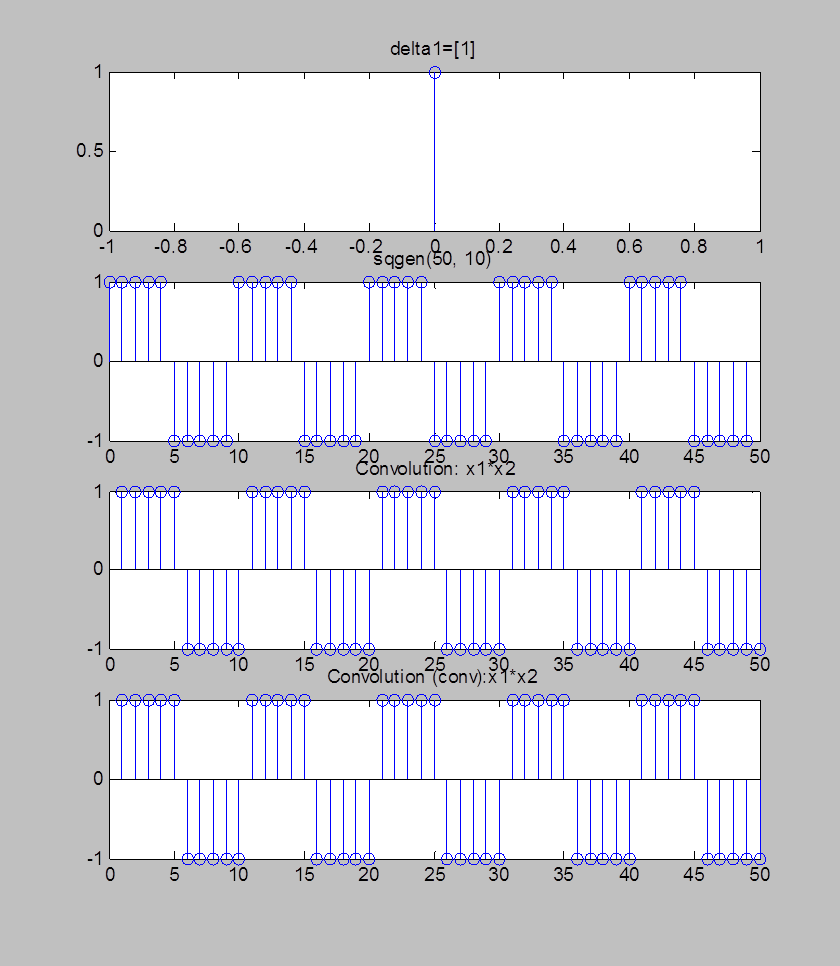
Рис.4. Графики единичного импульса, прямоугольной волны, их свёртки и свёртки, вычисленной с помощью функции conv()
Комментарий: Очевидно, что свертка сигналов в точности повторяет сигнал sqgen(50, 10). При каждом n значение свертки определяется как соответствующее значение сигнала sqgen(50, 10), умноженное на единицу, все остальные слагаемые свертки зануляются.
7. Генерирование delta2=[1 zeros(1,9)]. Свёртка delta2 и sqgen(50, 10).
Matlab script(labrab55.m)
T = 1; %шаг дискретизации
i = 0:1:49;
x1 = [1 zeros(1,9)]; %сигнал delta2=[1 zeros(1,9)]
x2 = sqgen(50,10); %генерированиепрямоугольнойволны
n1 = length(x1);
n2 = length(x2);
subplot(411), stem(0:9,x1), title('delta2=[1 zeros(1,9)]')
subplot(412), stem(i*T,x2), title(' sqgen(50,10)')
k1 = 1:n1+n2-1;
%вычисление свертки
for n = 1:n1+n2-1,
y(n) = 0;
for k = max(1,n+1-n1):min(n,n2),
y(n) = y(n)+sum(x1(n+1-k)*x2(k));
end
y(n) = y(n)*T;
end
%графиксверткисигналов
subplot(413), stem(k1*T,y), title(' Convolution: x1*x2')
%вычисление свертки с помощью функции conv()
subplot(414), stem(k1*T,T*conv(x1,x2)), title('Convolution (conv):x1*x2')
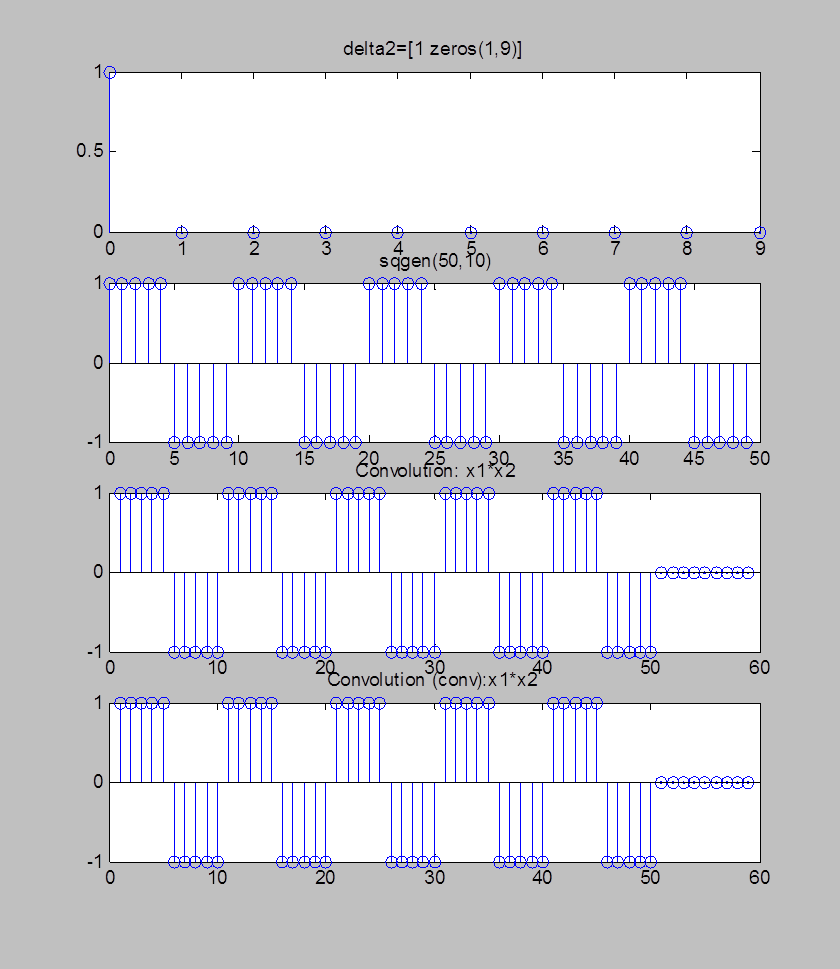
Рис.5. Графики delta2=[1 zeros(1,9)] сигнала, прямоугольной волны, их свёртки и свёртки, вычисленной с помощью функции conv()
Комментарий: Сравнивая рис.4 и рис.5 можно сказать, что при увеличении длительности сигнала длина свёртки также увеличивается вследствие того, что равна n1+n2-1, где n1 и n2- длины сигналов. В первом случае: длина первого сигнала – 1, длина второго – 50, следовательно длина свёртки – 50 (что можно наблюдать на рис.4), во втором случае (при дополнении нулями первого сигнала): длина первого сигнала – 10, длина второго сигнала – 50, длина свёртки – 59. Следовательно, всегда можно дополнить недостающие отсчеты одной из функций нулевыми отсчетами и уже от этих функций с другими длинами вычислить свертку. Последние 9 отсчётов свёртки принимают нулевые значения, т.к. со 2 по 10 отсчёты в первом сигнале - нули.
8. Генерирование плоского импульса с помощью команды h1=[ones(1,2)]. Свёртка h1 и sqgen(50, 10). Увеличение длины импульса до 8, свёртка полученного импульса и sqgen(50, 10).
Matlab script(labrab56.m)
T = 1; %шагдискретизации
i = 0:49;
x1 = [ones(1,2)];
x2 = sqgen(50,10);
n1 = length(x1);
n2 = length(x2);
subplot(311), stem(0:1,x1), title('h1=[ones(1,2)]')
subplot(312), stem(i*T,x2), title('sqgen(50, 10)')
k1 = 1:n1+n2-1;
%вычисление свертки с помощью функции conv()
subplot(313), stem(k1*T,T*conv(x1,x2)), title('Convolution (conv):x1*x2')
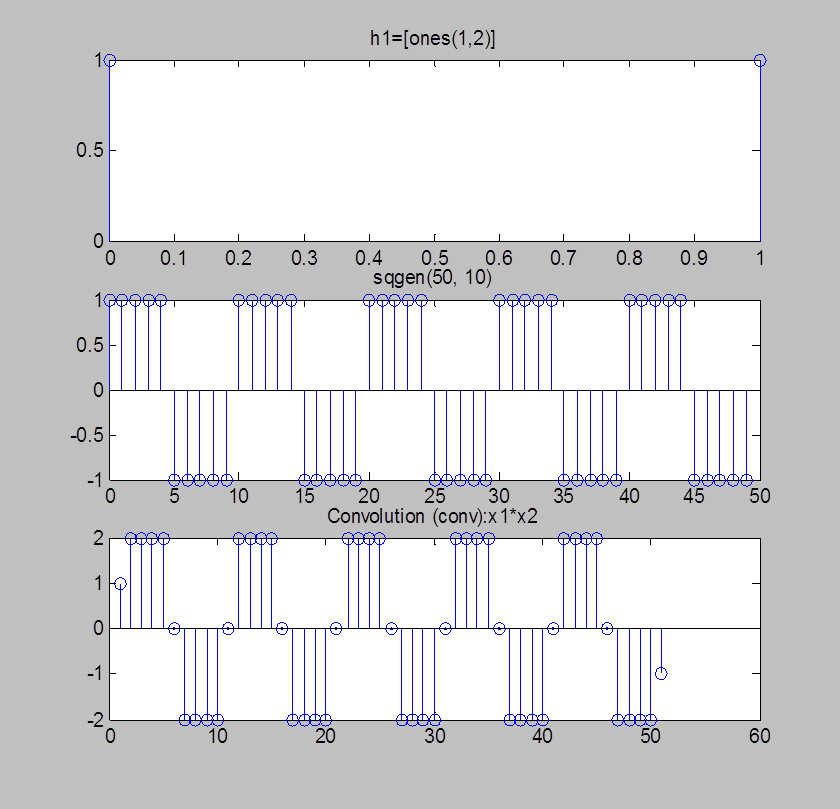
Рис.6. Графики h1=[ones(1,2)] сигнала, прямоугольной волны и их свёртки, вычисленной с помощью функции conv()
Matlab script(labrab57.m)
T = 1; %шаг дискретизации
i = 0:49;
x1 = [ones(1,8)];
x2 = sqgen(50,10);
n1 = length(x1);
n2 = length(x2);
subplot(311), stem(0:7,x1), title('h2=[ones(1,8)]')
subplot(312), stem(i*T,x2), title('sqgen(50, 10)')
k1 = 1:n1+n2-1;
%вычисление свертки с помощью функции conv()
subplot(313), stem(k1*T,T*conv(x1,x2)), title('Convolution (conv):x1*x2')
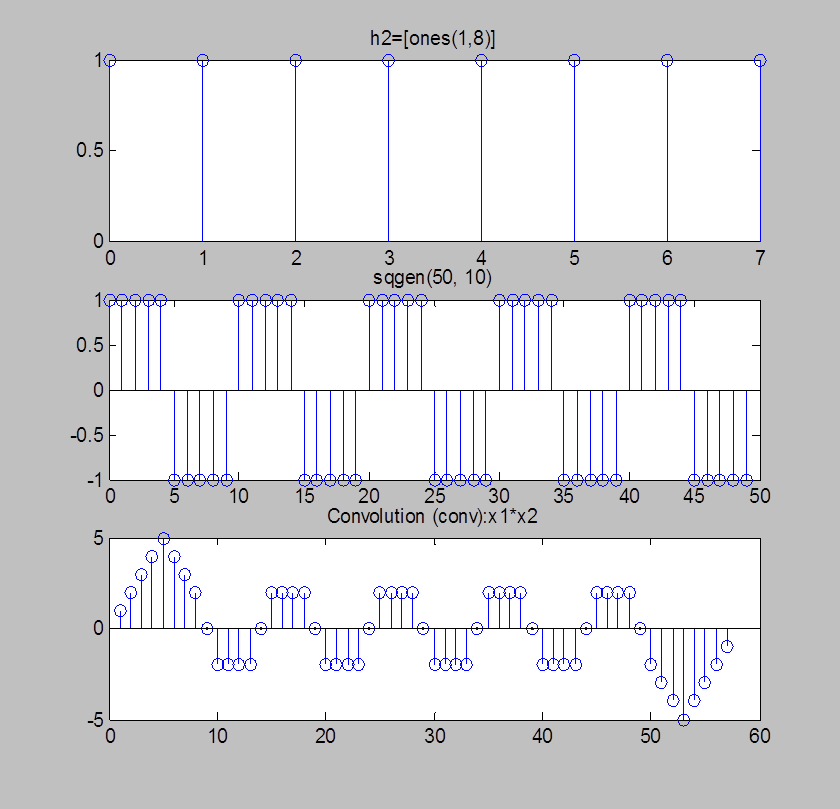
Рис.7. Графики h2=[ones(1,8)] сигнала, прямоугольной волны и их свёртки, вычисленной с помощью функции conv()
Комментарий: Сравнивая рис.6 и рис.7 можно сказать, что с увеличением длины первого сигнала свёртка меняет свой вид. В первом случае: длина первого сигнала – 2, длина второго – 50, следовательно длина свёртки – 51, во втором случае: длина первого сигнала – 8, длина второго сигнала – 50, длина свёртки – 57. Из рисунков видно, что также как и в предыдущих пунктах (п.2, п.3), если один из сигналов короче другого, то в результирующей свёртке меняют вид только передний и задний фронты (в начале отсчётов и в конце отсчётов (где количество отсчётов равно длительности первого сигнала, т.е. в первом случае – 2, во втором - 8)). На рис.7 видно, что значения первых и последних 8 отсчетов свертки равномерно увеличиваются и уменьшаются на 1 в зависимости от того положительные или отрицательные значения имеет сигнал sqgen(50, 10) в соответствующих отсчетах. На остальных отсчетах свертка представляет собой прямоугольную последовательность амплитуды 2 с нулевыми значениями в 9, 14, 19, 24, 29 и т.д. отсчетах. При увеличении длительности сигнала h1 вид свертки будет все больше приближаться к треугольной последовательности амплитуды 5, т.е. значение каждого последующего отсчета будет на 1 отличаться от предыдущего в зависимости от знака сигнала sqgen(50, 10) в соответствующем отсчете.
9. Вычисление свёртки сигналов
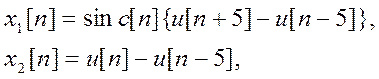
где 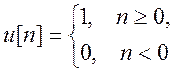 -
дискретная единичная ступенчатая функция.
-
дискретная единичная ступенчатая функция.
Восстановление сигнала ![]() из свертки с помощью функции deconv().
из свертки с помощью функции deconv().
[q, r] = deconv(z, x) – выполняет операцию, обратную свертке, результат сохраняется в векторе q, а остаток в векторе r , что Z=conv(x,q)+r.
Matlab function(fun.m)
%функция для определения единичной ступенчатой функции
function u=fun(t)
for i=1:length(t)
if t(i)>=0
u(i)=1;
end
if t(i)<0
u(i)=0;
end
end
Matlab script(labrab58.m)
T = 5;
t = -T:T; %определение временного интервала
tt = 0:25;
t1 = tt-5;
t2 = tt+5;
u = fun(tt); %определение функции u(t)
u1 = fun(t1); %определение функции u(t-5)
u2 = fun(t2); %определение функции u(t+5)
x1 = sinc(t/pi); %определение сигналов
x2 = u-u1;
x = conv(x1,x2); %вычисление свертки сигналов
subplot(4,1,1), stem(t,x1), title('x1');
subplot(4,1,2), stem(tt,x2), title('x2');
subplot(4,1,3), stem(x), title('Convolution (conv):x1*x2');
z = deconv(y,x2);
subplot(4,1,4), stem(t,z), title('deconvolution x2');
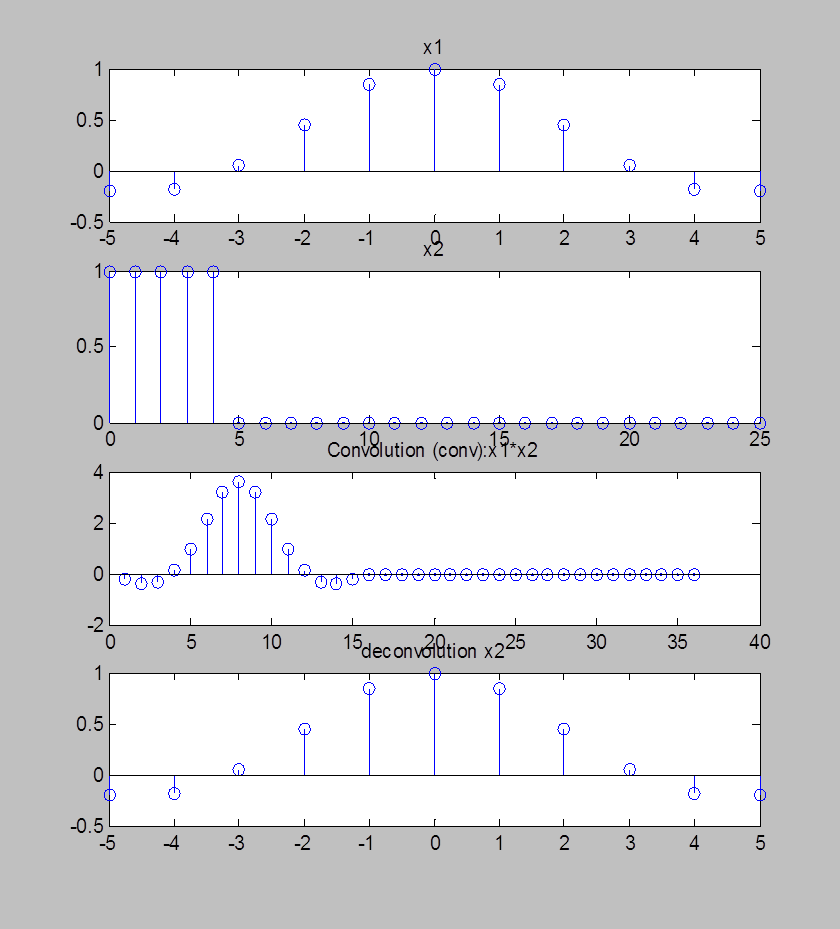
Рис.8. Графики
сигнала ![]() , сигнала
, сигнала ![]() ,
их свёртки, вычисленной с помощью функции conv()
и сигнала
,
их свёртки, вычисленной с помощью функции conv()
и сигнала ![]() , восстановленного
из свёртки с помощью функции deconv()
, восстановленного
из свёртки с помощью функции deconv()
Комментарий: Из
полученных графиков видно, что функция deconv()
действительно восстанавливает из свертки исходный сигнал ![]() . Значения сигнала
. Значения сигнала ![]() полностью восстановлены.
полностью восстановлены.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.