Изучение понятия и свойств непрерывной и дискретной свертки. Вариант 1, страница 3

10.       Генерирование экспоненциально убывающего дискретного сигнала длительностью 100 отсчетов и прямоугольного сигнала из 40 отсчетов. Вычисление  дискретной свертки этих сигналов и определение времени выполнения свертки. Вычисление свертки этих сигналов с помощью БПФ, определение времени её выполнения.  Вычисление обратного (инверсное) ДПФ свёртки.

Matlab script(labrab59.m)

t = 0:0.1:9.9;

t1 = 0:0.1:3.9;

t2 = 0:0.1:13.8;

t3 = 0:0.1:25.5;

y1 = exp(-t);

subplot(4,1,1), stem(t,y1),    axis([0,10, 0,1]), title('exp(t)')

y2 = rectpuls(t1-2,4);

subplot(4,1,2), stem(t1,y2), axis([0,4, 0,1]);     title('Rectangle impulse')

time1 = cputime;

y3 = conv(y1,y2);

time2 = (cputime-time1);

subplot(4,1,3), stem(t2,abs(y3)), axis([0, 14, 0, 12])

title('Convolution (conv)')

y4 = [y1 zeros(1,156)];

y5 = [y2 zeros(1,216)];

time3 = cputime;

y4p = fft(y4);

y5p = fft(y5);

y6 = y4p.*y5p;

y6p = ifft(y6);

time4 = (cputime-time3)

subplot(4,1,4), stem(t3,abs(y6p)),     title('Convolution (ifft)')

axis([0, 14, 0, 12]);

time2 = 0.068c

time4 = 0.017c

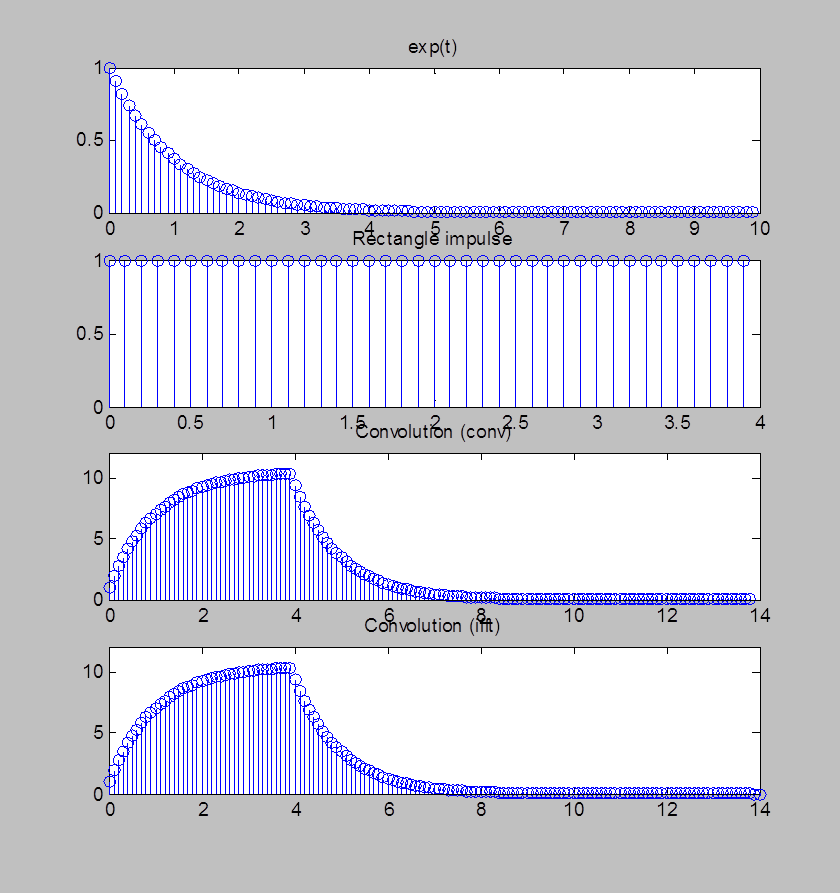
Рис.9. Графики экспоненциального сигнала, прямоугольного сигнала, их свёртки, вычисленной с помощью функции conv() и свёртки, вычисленной с помощью обратного ДПФ

Комментарий:          При вычислении свёртки с помощью функции conv() размер свертки – 139 отсчетов (100(количество отсчётов первого сигнала)+40(количество отсчётов второго сигнала)-1). Значения свертки, соответствующие первым 40 отсчетам,  равномерно увеличиваются (качественно напоминает зеркально отображённый экспоненциально убывающий сигнал), однако затем характер свертки меняется (экспоненциально убывающий сигнал), поскольку зануляются первые слагаемые при вычислении свертки. Размер круговой свертки равен размеру каждого из сигналов – 256 отсчетов. Первые 139 отсчетов в точности повторяют свертку, выполненную с помощью функции conv(). Следующие 117 отсчетов заполнены нулями. Дискретные преобразования Фурье являются периодическими, следовательно, и дискретная свертка тоже периодическая. Из-за периодического характера, когда одна последовательность при сдвиге выходит за крайнюю точку другой, возникает эффект “перекрытия”. Для того чтобы избежать перекрытия необходимо увеличивать период за счет увеличения  N, т.е. следует использовать ДПФ с N большим N₁ + N₂  - 1, для этого дополняют исходные последовательности нулевыми отсчётами. Этот метод вычисления свертки конечных последовательностей называется быстрой сверткой. Быстрая свертка эффективнее вычисления свёртки с помощью функции conv() в данном случае в 4  раза. Это обеспечивается за счет быстрых алгоритмов вычисления ДПФ. Ожидали получить результат выполнения быстрой свёртки порядка 9 раз быстрее (для вычисления ДПФ одного сигнала требуется порядка  операций, т.е. ускорение в 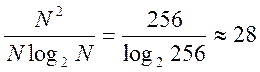 раз, т.к. вычисляем ДПФ двух сигналов и вычисляем их произведение, то ускорение равно порядка 9 раз), но из-за многозадачности ОС ускорение получилось меньше.

Вывод по работе:         В данной работе понятия непрерывной и дискретной свёртки приобрели практический смысл. Непрерывной свёрткой двух функций   и    называется интеграл вида 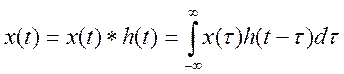. Сигнал зеркально отображается - , смещается на t - , далее умножается на сигнал  - и это выражение интегрируется -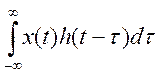. В данной работе были достигнуты следующие результаты:

1)  была вычислена непрерывная свёртка численным методом, при этом значения свертки, соответствующие отсчетам длительности первого импульса,  равномерно увеличиваются (и качественно напоминает зеркально отображённый экспоненциальный сигнал), однако затем характер свертки меняется, поскольку зануляются первые слагаемые при вычислении свертки. На рис.1 видно, что значения первых 10 отсчётов и отсчетов от 20 до 30 свертки равномерно увеличиваются и уменьшаются. На отсчетах от 10 до 20 свертка представляет собой прямоугольный импульс, а от 30 до 99 нулевые значения;

2)  была вычислена дискретная свёртка сигналов, при этом свертка y получалась в виде последовательности длины n1 + n2 -1 (n1 – длина первой последовательности, а n2 – длина второй последовательности), k-й элемент которой определялся по формуле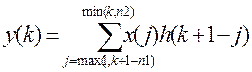. Очевидно, что при увеличении длительности сигнала длина свёртки также увеличивается. В п.6: длина первого сигнала – 1, длина второго – 50, следовательно длина свёртки – 50 (при этом первый сигнал представляет собой единичный импульс, а второй – прямоугольную волну, и свёртка будет полностью повторять второй сигнал, т.к. при  каждом k значение свёртки определяется как соответствующее значение прямоугольной волны умноженное на единицу, все остальные слагаемые свёртки зануляются), в п.7(при дополнении нулями первого сигнала): длина первого сигнала – 10, длина второго сигнала – 50, длина свёртки – 59(первые 50 отсчётов – прямоугольная волна, а последние 9 – заполнены нулями, т.к. в первом сигнале со второго по десятый отсчёты - нули);

3)  при вычислении дискретной свёртки единичной функции и прямоугольной волны было показано, что при увеличении длительности сигнала единичной функции вид свертки будет все больше приближаться к треугольной последовательности амплитуды 5 (значение каждого последующего отсчета будет на 1 отличаться от предыдущего в зависимости от знака сигнала прямоугольной волны в соответствующем отсчете), и в свёртке будут менять вид только передний и задний фронты;

4)  восстановление сигнала из свёртки можно осуществить с помощью встроенной функции deconv();

5)  было получено, что при использовании быстрой свёртки время вычисления уменьшается, в данном случае при количестве отсчётов 256 время вычислений уменьшилось в 4 раза.

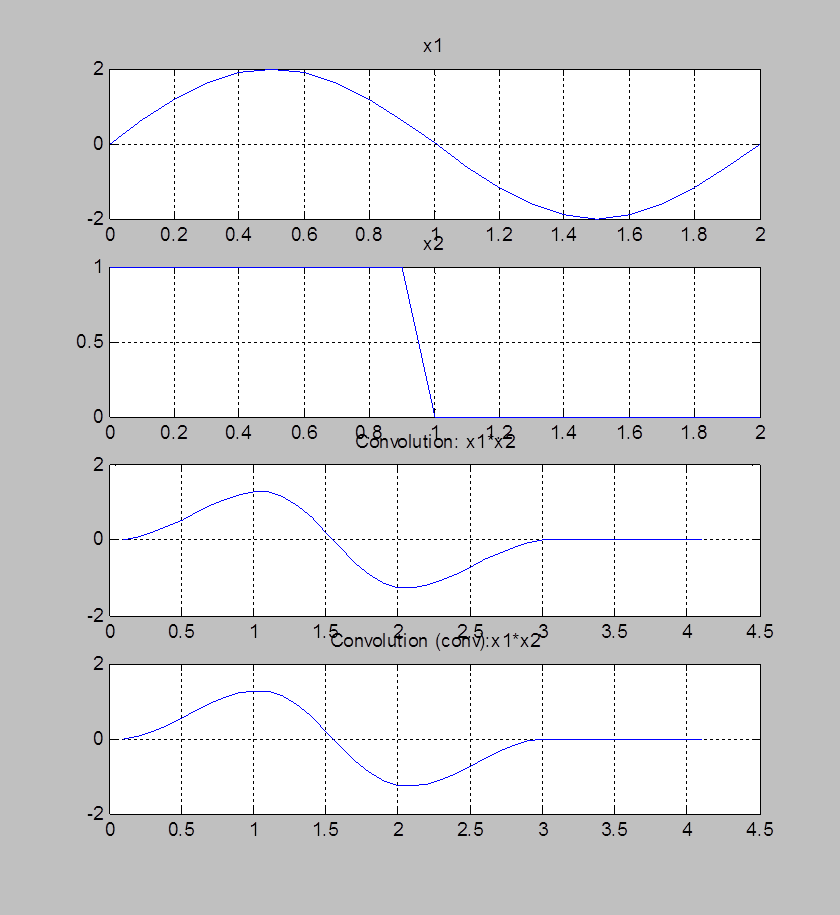
T = 0.1;                                                                                                           %шаг дискретизации  

i = 0:20;

x1 = 2*sin(i*pi*T);                             %сигнал x1

x2 = rectpuls(i-5,10);                                      %сигнал x2

n1 = length(x1);

n2 = length(x2);

subplot(411),  plot(i*T,x1), title('x1'),grid

subplot(412),  plot(i*T,x2), title('x2'),grid

k1 = 1:n1+n2-1;

%вычисление  свертки

for  n = 1:n1+n2-1,

y(n) = 0;

   for k = max(1,n+1-n1):min(n,n2),

      y(n) = y(n)+sum(x1(n+1-k)*x2(k));

   end

y(n) = y(n)*T;  

end

%график свертки сигналов

subplot(413), plot(k1*T,y),title(' Convolution: x1*x2'),grid

%вычисление свертки с помощью функции conv()

subplot(414), plot(k1*T,T*conv(x1,x2))

title(' Convolution (conv):x1*x2'),grid