НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
КАФЕДРА СИСТЕМ СБОРА И ОБРАБОТКИ ДАННЫХ
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 5
НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ СВЕРТКИ
Вариант №4
Студент: Чуркаев А.А.
Группа: АО-61
Преподаватель: доц. Щетинин Ю.И.
Новосибирск
2008
Цель работы: Изучение понятия и свойств непрерывной и дискретной свертки, приобретение практических навыков вычисления свертки в среде Matlab.
1.
Свертка двух непрерывных по времени сигналов (непрерывная
свертка) определяется выражением
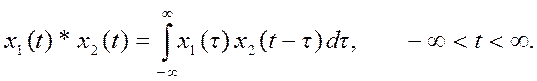
Численное вычисление непрерывной свертки может быть аппроксимировано конечной
суммой вида
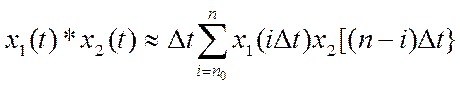 ,
,
где ![]() - интервал (шаг)
дискретизации.
- интервал (шаг)
дискретизации.
Процедура (файл-сценарий Matlab) для приближенного вычисления
непрерывной свертки сигнала прямоугольной формы и экспоненциального сигнала:
% Численное вычисление непрерывной свертки
T=0.1; % шаг дискретизации
a=5;
i=0:50;
x1=exp(-a*i*T); % сигнал x1
x2=rectpuls(i-10,20); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(i*T,x1), title('x1')
subplot(412), plot(i*T,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y),title('Свертка x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
title('Вычисление с помощью conv')
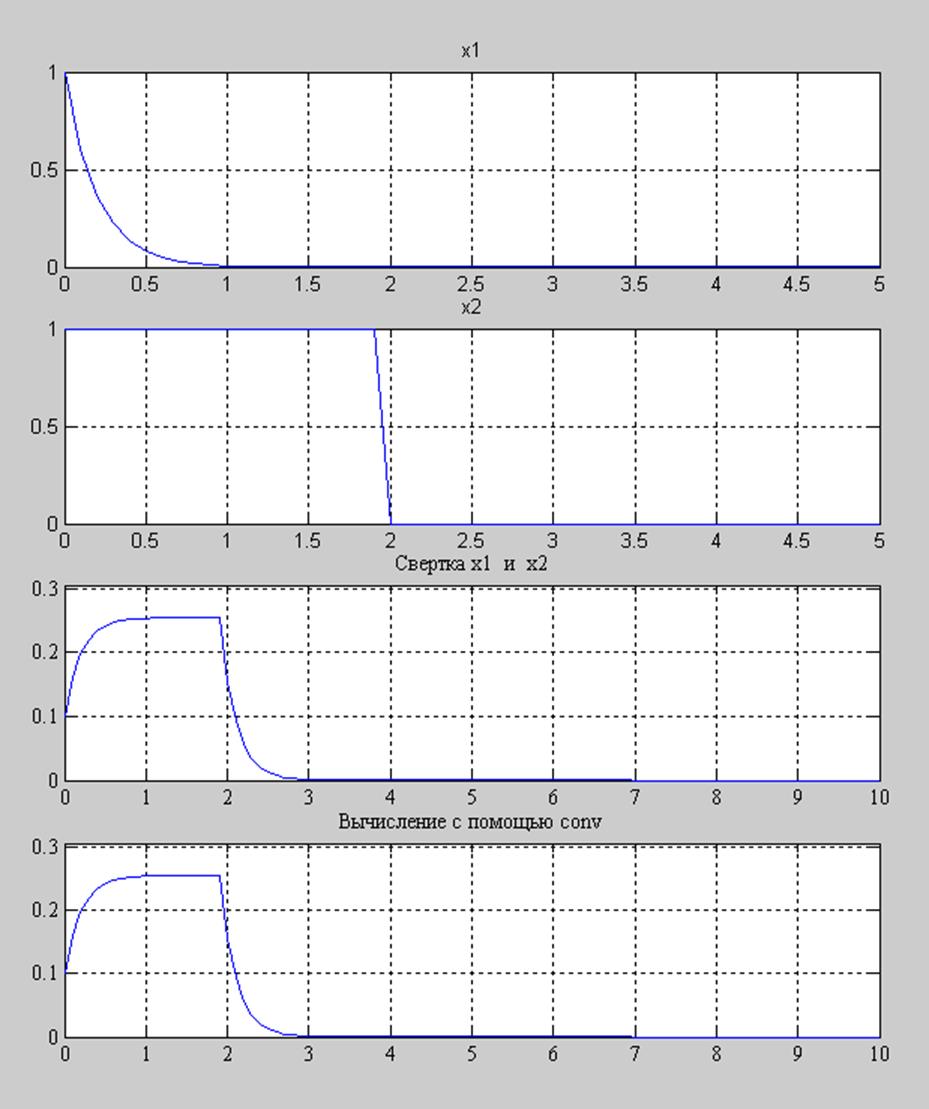
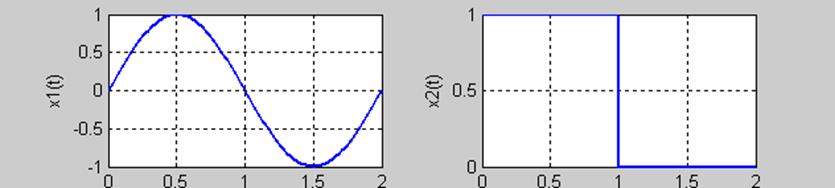
Рис. 1. Графики экспоненциального сигнала; прямоугольного сигнала; результата свертки, вычисленного в циклах; результата свертки, вычисленного функцией conv().
Комментарий:
Графики сверток, полученные с помощью конечных сумм и с помощью функции conv() совпадают. Функция conv() вычисляет свертку перемножением преобразований Фурье заданных сигналов и находит обратное преобразование. Свертка сигналов во временной области соответствует произведению преобразований Фурье этих сигналов в частотной области.
2. Вычисление непрерывной свертки прямоугольного сигнала и синусоиды.
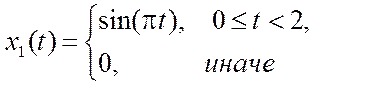
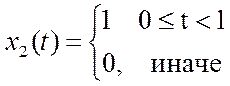
% Численное вычисление непрерывной свертки
T=0.1; % шаг дискретизации
a=5;
i=0:20;
x1=sin(pi*i/10); % сигнал x1
x2=rectpuls(i-5,10); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(i*T,x1), title('x1')
subplot(412), plot(i*T,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y), set(gca, 'Fontname', 'Times New Roman Cyr', 'FontSize',12)
title('Свертка x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
set(gca, 'Fontname', 'Times New Roman Cyr', 'FontSize',12)
title('Вычисление с помощью conv')
xlabel('сек')
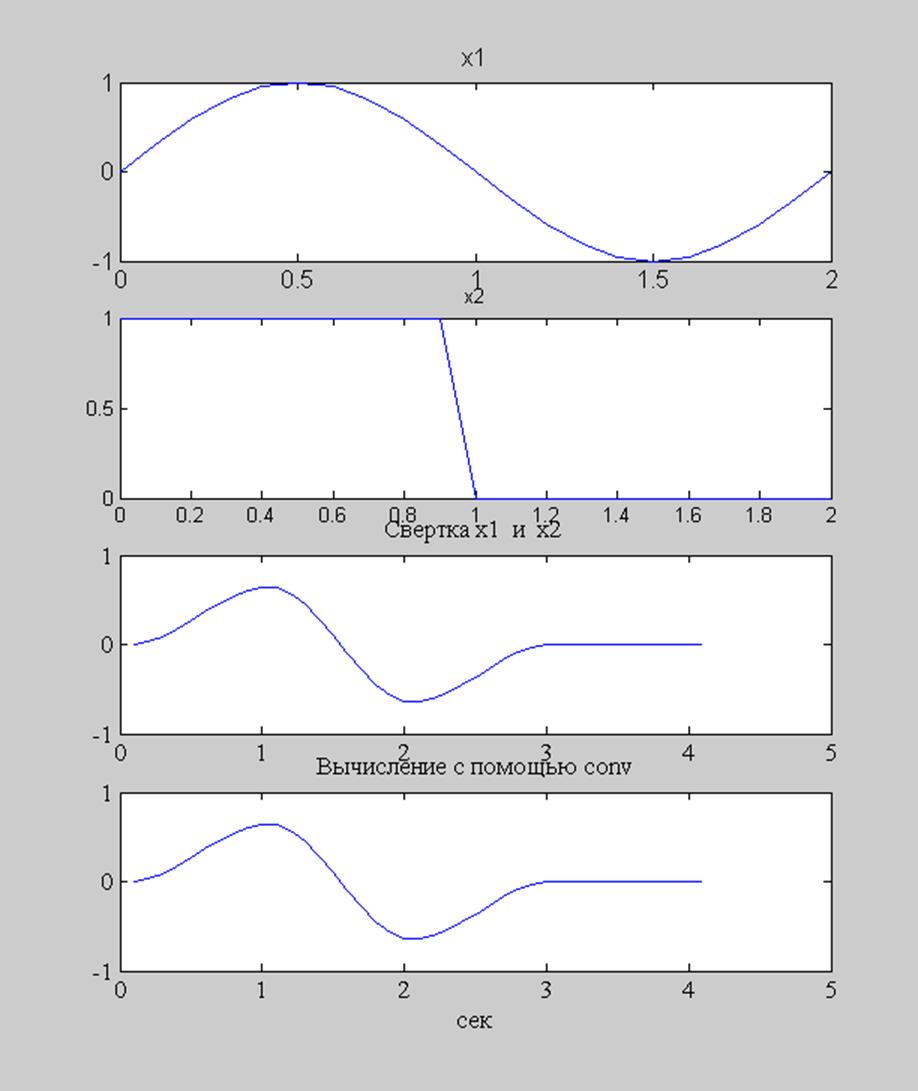
Рис. 2. Графики прямоугольного сигнала, синусоиды, результата свертки, вычисленного в циклах и результата свертки, вычисленного функцией conv().
3. Функция sqgen(L,T), которая генерирует прямоугольную последовательность импульсов (прямоугольную волну) длиной L отсчетов и периодом T отсчетов.
Листинг функции sqgen(L,T)
% функция sqgen() предназначена для генерации прямоугольных
% последовательностей импульсов, длиной L отсчетов и периодом T отсчетов
function [x,t] =sqgen(L,T)
t=0:1:L;
x=square(2*pi*t/T);
stem(t,x);
4. Вычисление свертки единичного импульса и прямоугольной последовательности импульсов.
Ниже приведен код программы, с помощью которого была построена свертка прямоугольной волны и дельта–функции:
%вычисление свертки единичного импульса и прямоугольной
%последовательности импульсов.
[x t]=sqgen(50,10);
delta1=[1];
con=conv(x,delta1);
subplot(311), stem(t,x);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title('Прямоугольная волна'); grid;
axis([0 max(t) 1.2*min(x) 1.2*max(x)]);
subplot(312), stem(0,delta1);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title('Дельта - функция'); grid
subplot(313), stem((0:length(con)-1),con);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title('Свертка прямоугольной волны и дельта - функции'); grid
axis([0 (length(con)-1) 1.2*min(con) 1.2*max(con)]);
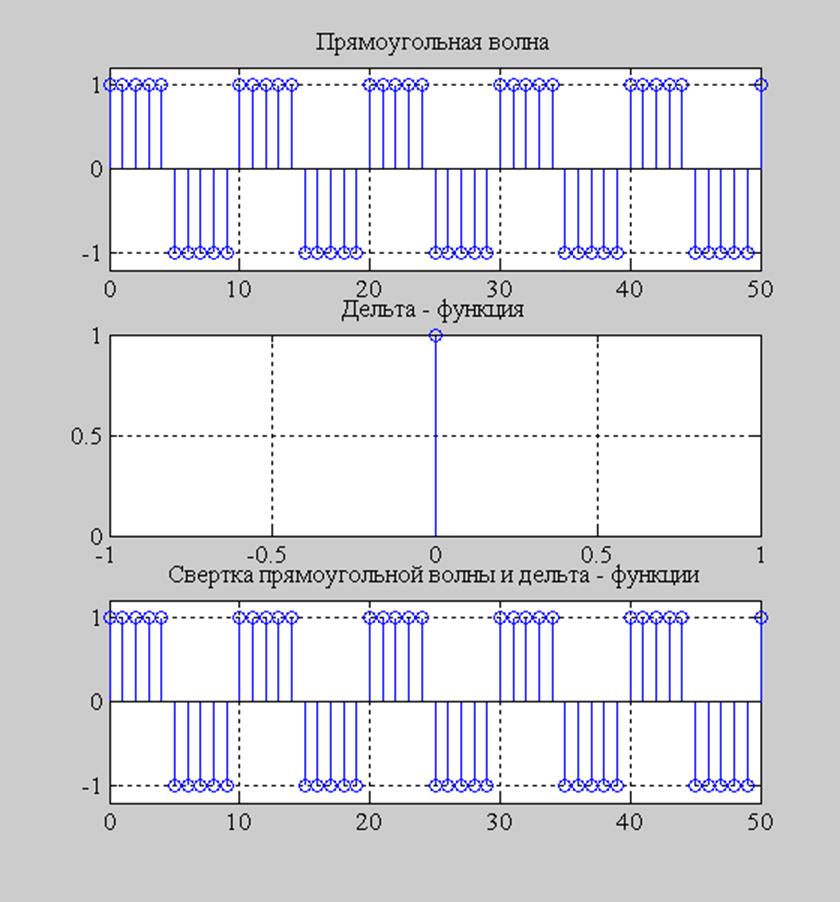
Рис. 3. График прямоугольной волны, дельта-функции, свертка прямоугольной волны и дельта-функции.
Комментарий:
Видно, что, если один из сигналов, участвующих в свертке, представляет собой дельта-функцию, то эта свертка в точности повторяет другой сигнал. В реальных системах сигнал не может представлять собой дельта-функцию, т.к. амплитудный спектр дельта-функции является прямой линией на любой частоте, а это не может быть достигнуто в реальной системе.
5. Вычисление свертки единичного импульса дополненного нулями справа и прямоугольной последовательности импульсов.
Ниже приведен код программы, с помощью которого была построена свертка прямоугольной волны и дельта – функции, дополненной нулями справа:
T=10;
[x t]=sqgen(50,T);
delta2=[1 zeros(1,9)];
con=conv(x,delta2);
subplot(311), stem(t,x);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title('Прямоугольная волна');
axis([0 max(t) 1.2*min(x) 1.2*max(x)]); grid;
subplot(312), stem(0:9,delta2);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.