НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
КАФЕДРА СИСТЕМ СБОРА И ОБРАБОТКИ ДАННЫХ
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 2
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
ПЕРИОДИЧЕСКИХ СИГНАЛОВ
Вариант №10
Группа: АТ-53
Студентка: Пяткова Д.А.
Преподаватель: Щетинин Ю.И.
Новосибирск
2007 г.
Цель работы:изучение понятия спектра периодического сигнала, приобретение практических навыков вычисления и построения графиков спектров сигналов в среде MATLAB.
Задание варианта №10
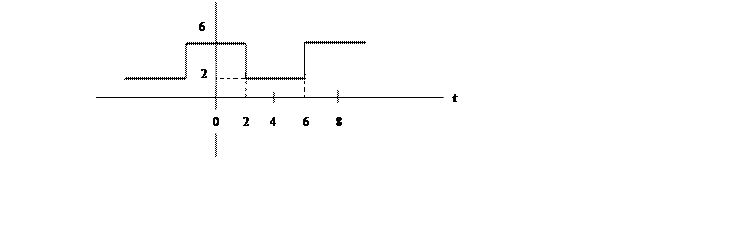
Рис 1. Исходный сигнал
Ряд Фурье
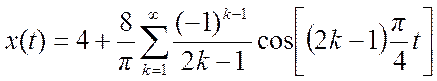
2.
Получение коэффициентов разложения в комплексный ряд Фурье для заданного сигнала.
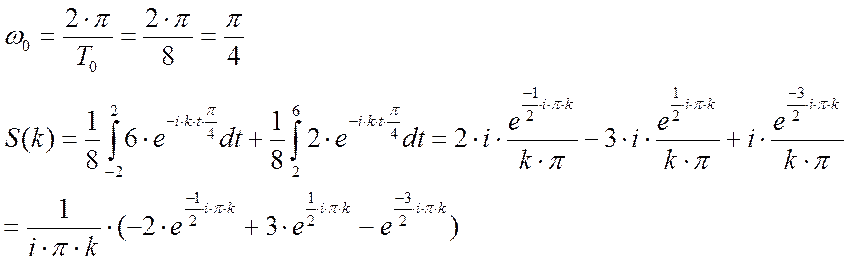
Запишем комплексный ряд Фурье:
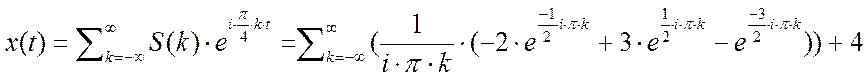
Построены графики амплитудного и фазового спектров сигнала
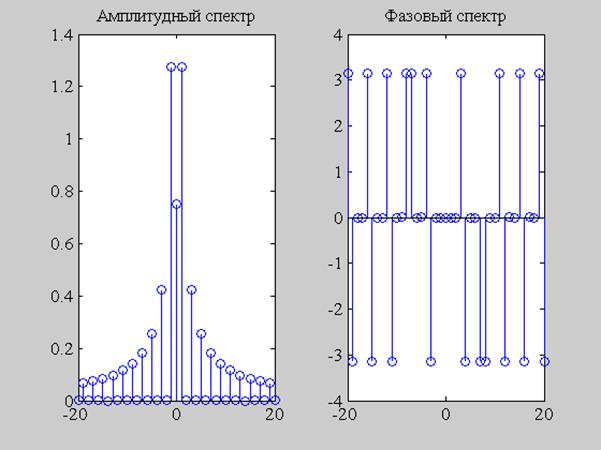
Рис. 2 Графики амплитудного и фазового спектра
Видим, что чем больше частота, тем меньше амплитуда колебаний,
поэтому мы можем брать интервал не от ![]() ,
а гораздо меньше. При этом нужно учесть, что чем меньший интервал мы выберем,
тем больше будет не соответствие с реальным сигналом (погрешность наших
расчетов). Так же из АЧХ видим, что при n кратному двум
амплитуда (значит, сдвиг фаз тоже) равна нулю, покажем это аналитически:
,
а гораздо меньше. При этом нужно учесть, что чем меньший интервал мы выберем,
тем больше будет не соответствие с реальным сигналом (погрешность наших
расчетов). Так же из АЧХ видим, что при n кратному двум
амплитуда (значит, сдвиг фаз тоже) равна нулю, покажем это аналитически:
Пусть n=2
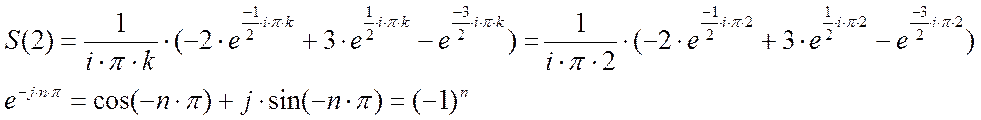
Получаем:
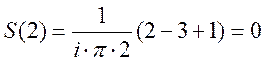
3. М-файл для построения графиков амплитудного и фазового спектров сигнала.
n1=1:20;
cn=((-2)*exp(j.*n1*pi*(-1)/2)+3*exp(j.*n1*pi/2)-exp(j.*n1*pi*(-3)/2))./(j*pi*n1);
%воспроизводим сумму ряда с положительными n
n2=-20:-1;
c_n=((-2)*exp(j.*n2*pi*(-1)/2)+3*exp(j.*n2*pi/2)-exp(j.*n2*pi*(-3)/2))./(j*pi*n2);
%воспроизводим сумму ряда с отрицательными n
Cn=[ c_n 3/4 cn];
n3=[n2 0 n1];
n=-20:20;
figure(1), subplot(121),stem(n,abs(Cn));
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title('Амплитудный спектр');
subplot(122),stem(n,angle(Cn));
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title('Фазовый спектр');
4. Определение коэффициентов ряда Фурье с помощью функции fft() для заданного сигнала.
М-файл, с помощью которого были проведены расчёты и построенные графики:
T=8; % период сигнала
N=63;
t=0:T/N:T; % временной интервал
x=rectpuls(t,2)+rectpuls(t,4); % генерирование сигнала
figure(1),subplot(311), plot(t,x) % график сигнала
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,8);
title(' График сигнала')
k=1:N;
C=((-2)*exp(j.*k*pi*(-1)/2)+3*exp(j.*k*pi/2)-exp(j.*k*pi*(-3)/2))./(j*pi*k); % коэффициенты ряда Фурье
% график амплитудного спектра
subplot(312),
stem(2*pi*k/T, abs(C));
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,8);
title(' Амплитудный спектр сигнала')
y=fft(x,N); % Дискретное преобразование Фурье сигнала
subplot(313), stem(2*pi*k/T, abs(y)/(N+1))
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,8);
xlabel(' Угловая частота, рад/сек')
title(' Амплитудный спектр сигнала по процедуре fft')
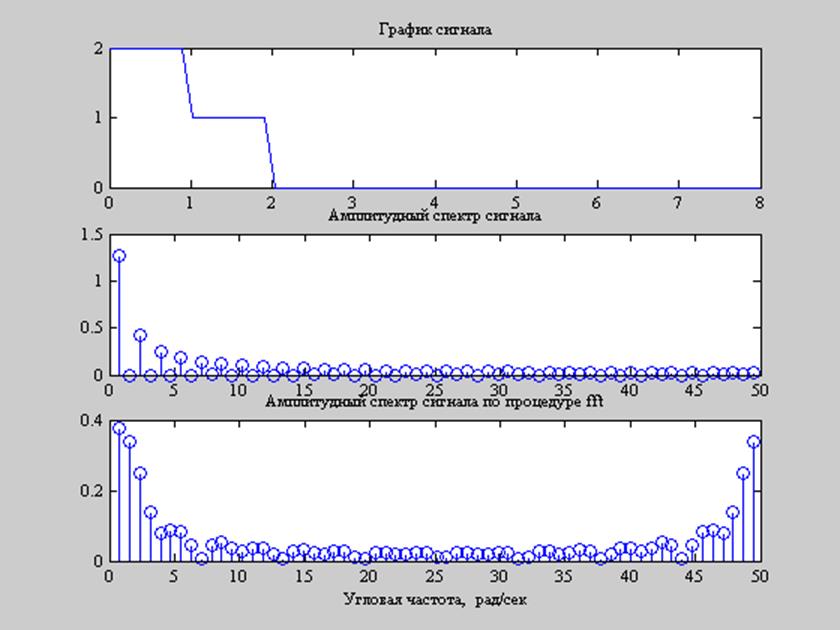
Рис.3
На рис.2 изображен сверху вниз: исходный сигнал, амплитудный спектр сигнала(вычисленный в “ручную”, т.е. коэффициенты ряда Фурье найдены аналитически), амплитудный спектр сигнала с помощью процедуры fft
5. Исследование сходимости ряда Фурье к исходному периодическому сигналу. Явление Гиббса
М-файл с помощью, которого были построены графики с четырьмя разными числами членов ряда.
T=8;
w0 = 2*pi/T;
t = 0:T/1000:T;
N = input('Введите минимальное число членов ряда ');
N=N*8;
c0 = 4;
x = c0*ones(1,length(t)); % постоянная составляющая
for n=1:N,
cn =((-2)*exp(j.*n*pi*(-1)/2)+3*exp(j.*n*pi/2)-exp(j.*n*pi*(-3)/2))./(j*pi*n);
c_n=conj(cn);
x = x + cn*exp(j*n*w0*t)+ c_n*exp(-j*n*w0*t);
end
figure(1), subplot(2,2,1), plot(t,x), grid
title(['N = ',num2str(N)]);
N=N/2;
x = c0*ones(1,length(t)); % постоянная составляющая
for n=1:N,
cn =((-2)*exp(j.*n*pi*(-1)/2)+3*exp(j.*n*pi/2)-exp(j.*n*pi*(-3)/2))./(j*pi*n);
c_n=conj(cn);
x = x + cn*exp(j*n*w0*t)+ c_n*exp(-j*n*w0*t);
end
subplot(2,2,2), plot(t,x), grid
title(['N = ',num2str(N)]);
N=N/2;
x = c0*ones(1,length(t)); % постоянная составляющая
for n=1:N,
cn =((-2)*exp(j.*n*pi*(-1)/2)+3*exp(j.*n*pi/2)-exp(j.*n*pi*(-3)/2))./(j*pi*n);
c_n=conj(cn);
x = x + cn*exp(j*n*w0*t)+ c_n*exp(-j*n*w0*t);
end
subplot(2,2,3), plot(t,x), grid
title(['N = ',num2str(N)]);
N=N/2;
x = c0*ones(1,length(t)); % постоянная составляющая
for n=1:N,
cn =((-2)*exp(j.*n*pi*(-1)/2)+3*exp(j.*n*pi/2)-exp(j.*n*pi*(-3)/2))./(j*pi*n);
c_n=conj(cn);
x = x + cn*exp(j*n*w0*t)+ c_n*exp(-j*n*w0*t);
end
subplot(2,2,4), plot(t,x), grid
title(['N = ',num2str(N)]);
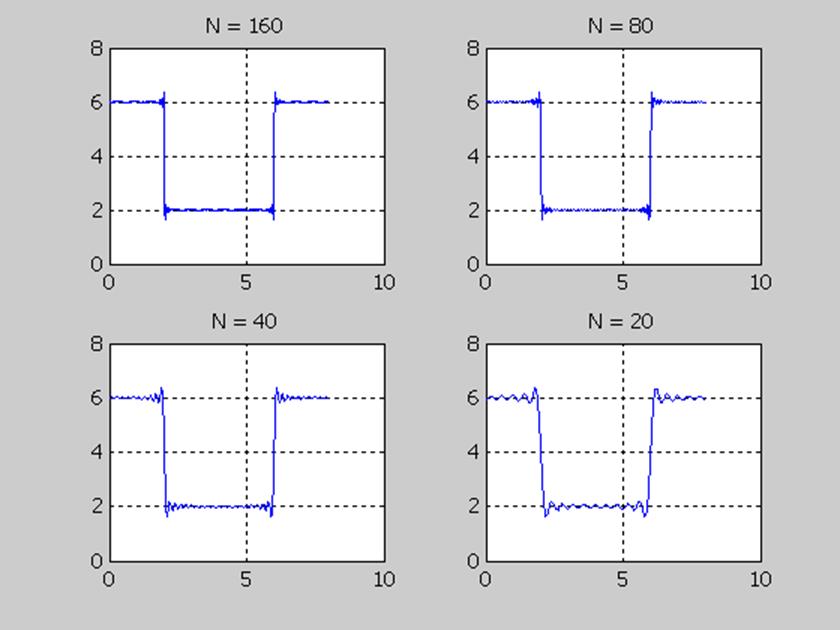
Рис 4.
На рисунке 4 изображены графики исходного сигнала. Для его аппроксимации использовалось различное число членов ряда Фурье.
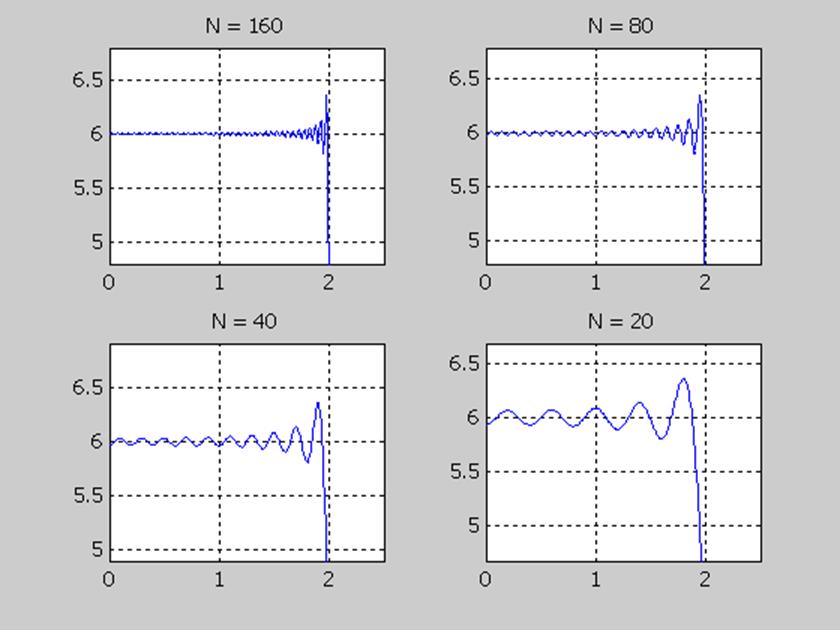
Рис 5.
На рисунке 5 изображены увеличенные части графиков (там где сигнал достигает своего максимума) представленных на рисунке 4. При увеличение числа членов ряда мы добиваемся лучшей аппроксимации, но при этом амплитуда не уменьшается, а только увеличивается частота гармоник из которых состоят пульсации.
6. Аппроксимация сигналов: квадратной волны, ноты Ре, ноты До.
Ниже приведен код с помощью которого производилась аппроксимация квадратной волны, а так же сгенерирована нота Ре. Последняя строка позволяет прослушать нам сгенерированные сигналы и звуки.
T=1/293.66;
w0 = 2*pi/T;
t = 0:1/8192:2;
x = zeros(1,length(t));
for n=1:2:19,
x = x + 4*sin(w0*n*t)/(pi*n);
end
y=harmonic(w0, 2*pi*8192, 2);
figure(1),plot(t(1:100),x(1:100),t(1:100),y(1:100)) , grid
axis([0 0.012 -1.5 1.5]);
p = zeros(1,length(t)); p=[x p y];
sound(p);
Функция harmonic
function [x, t] = harmonic(omega0, omegas, dur)
%harmonic генерирует гармонический сигнал, где
%omega0- угловая частота гармоники,рад/с,
%omegas-угловая частота отсчетов, рад/с,
%dur- продолжительность сигнала.
t = 0:2*pi/omegas:dur;
x =cos(omega0*t);
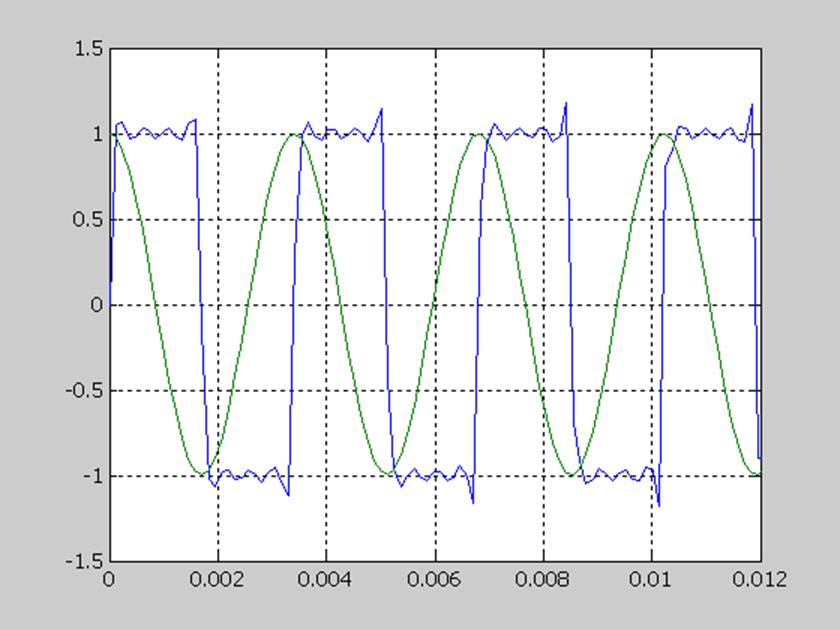
Рис.6
На рисунке 3 изображены графики: квадратной волны(аппроксимация) и гармонических колебаний.
Из графиков видно что максимумы квадратной волны и гармонических колебаний совпадают, хотя в промежутках между максимами функции значительно различаются (на высоту двух амплитуд).
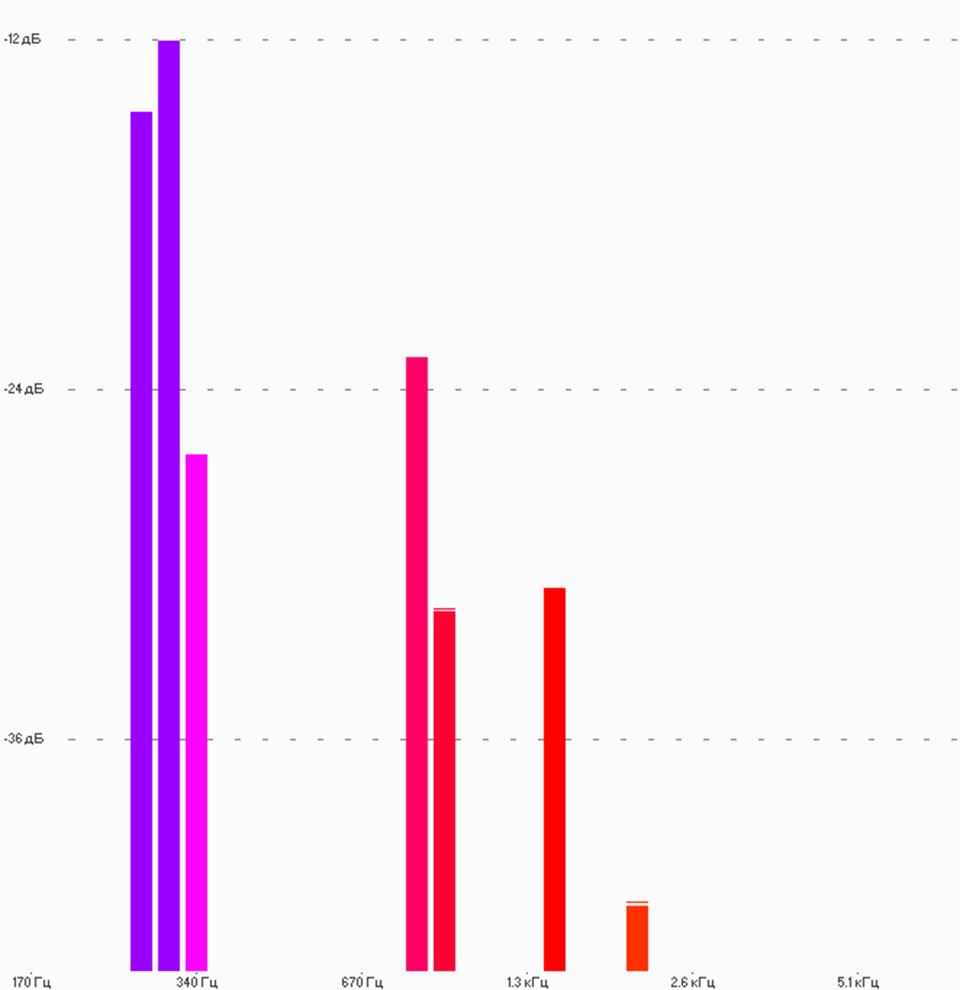
Рис.4
На рисунке 4 изображена АЧХ звукового сигнала в форме гармонической волны(нота Ре).
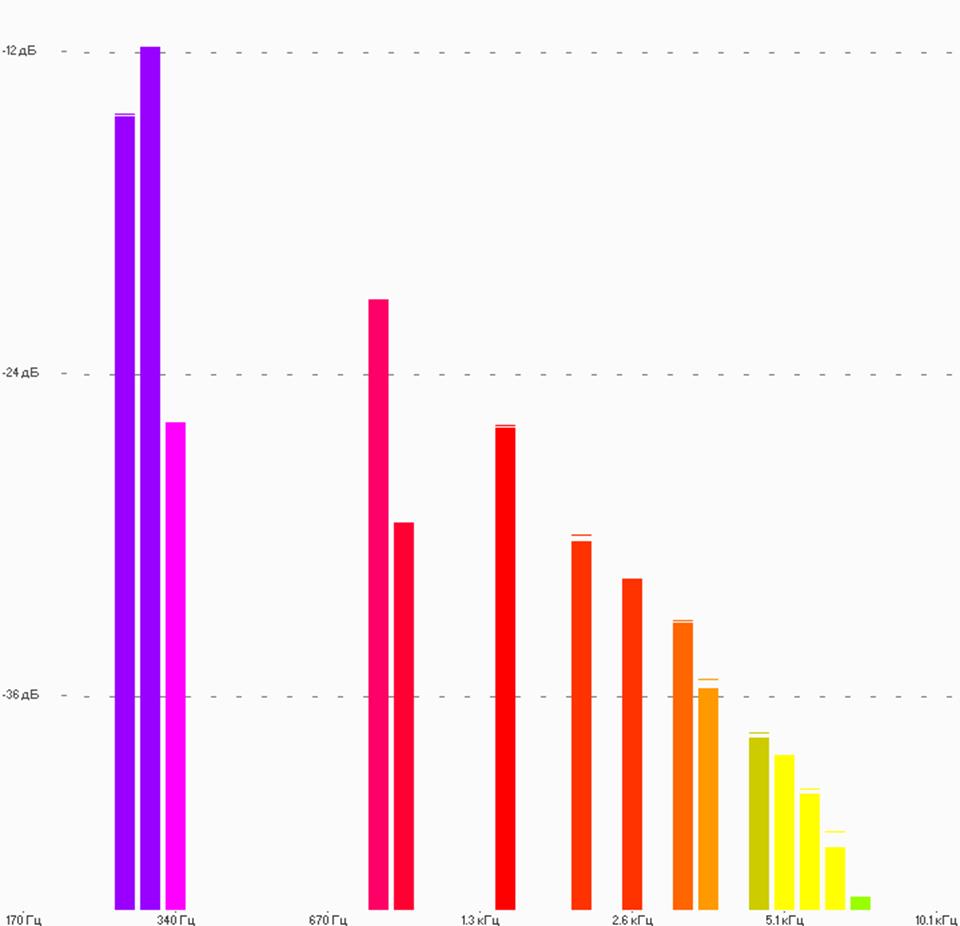
Рис.5
На рисунке 5 изображена АЧХ звукового сигнала в форме квадратной волны.
Как мы можем судить из спектра: у квадратной волны спектр шире чем у гармонической волны, т.к. для того что бы воспроизвести квадратную волну необходимо несколько гармонических колебаний с различными частотами.
Далее представлен код с помощью которого сгенерировано звучание ноты До первой октавы на фортепиано.
T=1/261.63;
w0 = 2*pi/T;
t = 0:1/8192:2;
do = zeros(1,length(t));
k=[1 0.5 0.5 -0.3 0.2];
for n=1:5,
do = do + k(n)*sin(n*w0*t);
end
subplot(211), plot(t(1:100),do(1:100)) , grid
axis([0 0.012 -1.5 1.5]);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title('График ноты До');
N=123; s=0:N;
y=fft(do,N+1);
subplot(212), stem(2*pi*s/T, abs(y)/(N+1)), grid
axis([0 max(2*pi*s/T)/2 0 max(abs(y)/(N+1))]);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
xlabel(' Угловая частота, рад/сек')
title(' Амплитудный спектр ноты До по процедуре fft')
sound(do);
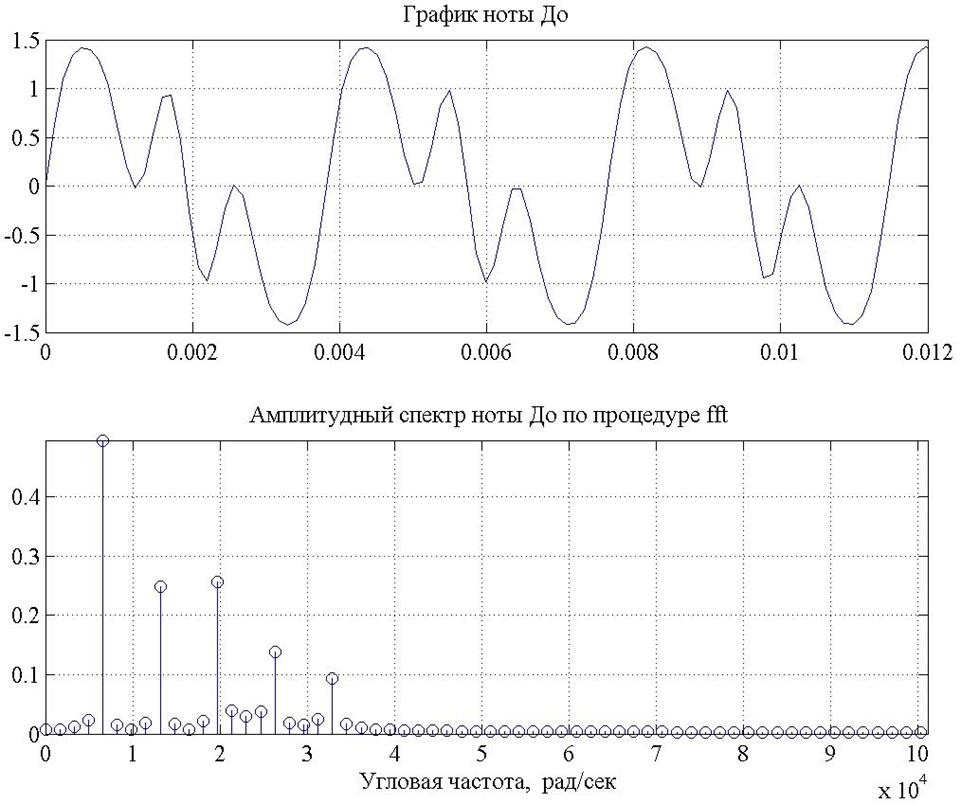
Рис. 6
На рисунке 6 приведен график ноты До и АЧХ
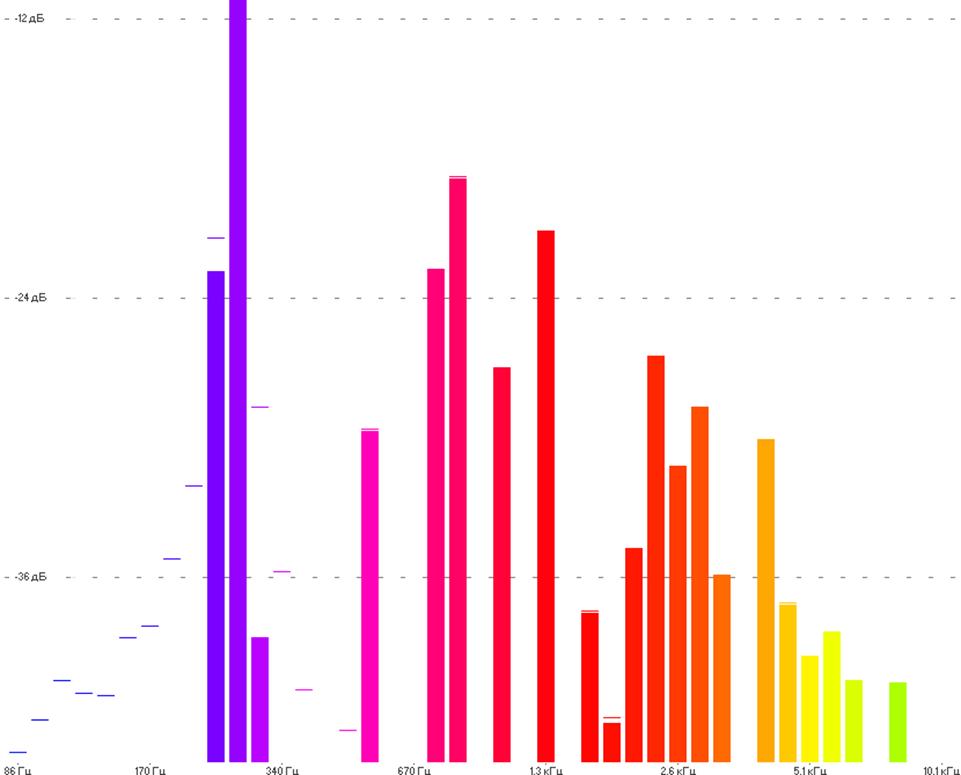
Рис.7
На рисунке 7 изображена АЧХ звукового сигнала в форме гармонической волны(нота До).
7. Генерирование исходного периодического сигнала с помощью приложения Simulink..
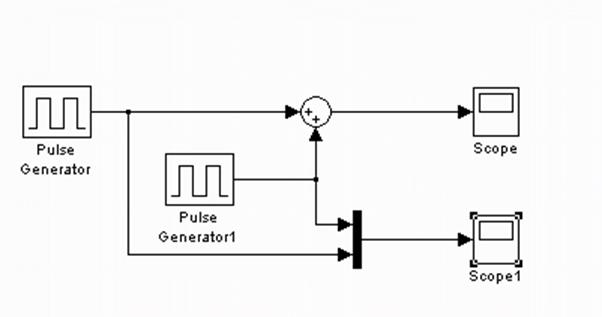
Рис.8
На рисунке 8 изображена схема, которая была собрана в приложение Simulink для генерирования исходного сигнала
Параметры генерирования:
Pulse Generator: Amplitude:1, Period(secs):4, Pulse Width (% of period):25, Phase delay(secs):0
Pulse Generator1: Amplitude:1, Period(secs):4, Pulse Width (% of period):50, Phase delay(secs):0
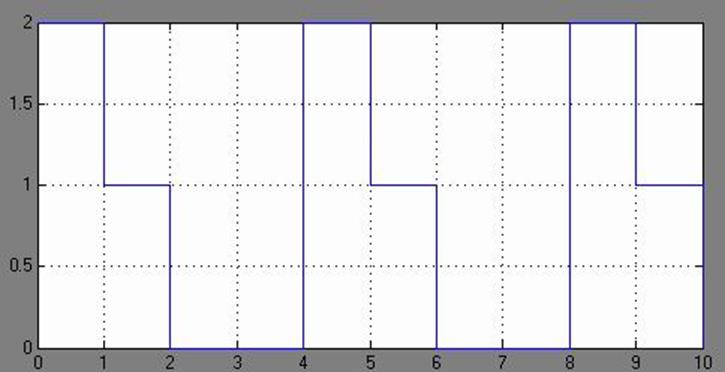
Рис.9
На рисунке 9 изображен график, который получается на осциллографе при суммирование двух прямоугольных импульсов, т.е. на осциллографе с названием “Scope”
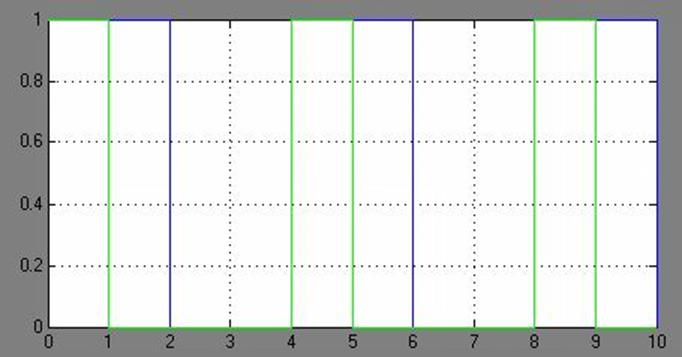
Рис.10
На рисунке 10 изображен график, который получается на осциллографе при параллельной подаче двух прямоугольных импульсов, т.е. на осциллографе с названием “Scope1”
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.