НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Спектральные представления непрерывных периодических сигналов
|
Факультет: АВТ Группа: АИ-22 Студент: Незнахина Е. Преподаватель: Щетинин Ю.И. |
Новосибирск-2004
Цель работы:изучить понятия спектра периодического сигнала, приобрести практические навыки вычисления и построения графиков спектров сигналов в среде MATLAB.
Задание 1.
Познакомиться с разложением в ряд Фурье периодических непрерывных сигналов и понятиями амплитудного и фазового спектров сигнала.
Задание 2.
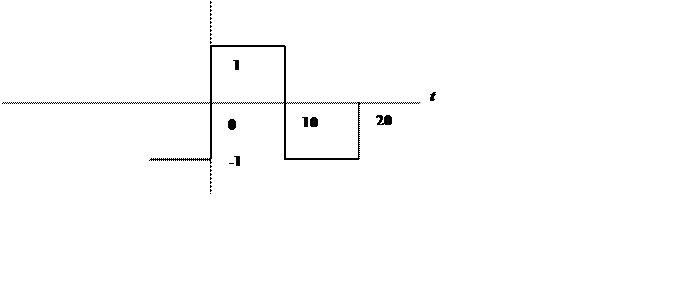
Получить аналитически коэффициенты разложения в комплексный ряд Фурье для сигнала. Построить график амплитудного спектра сигнала.
Ряд Фурье 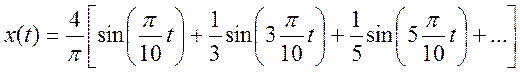
Характеристики сигнала:
Период
Т = 20, частота основной гармоники 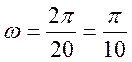
Коэффициенты комплексного ряда Фурье:
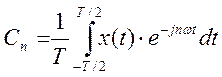
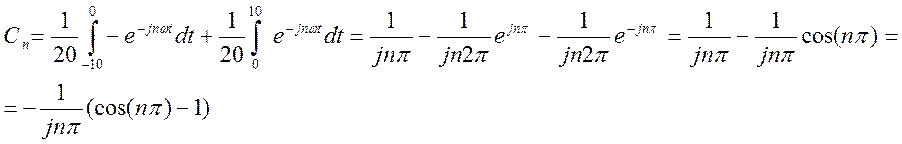
Ряд Фурье в комплексной форме выглядит так:
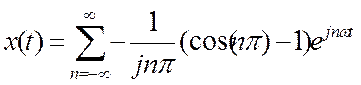
Задание 3.
Написать и выполнить файл-сценарий, позволяющий построить графики амплитудного и фазового спектров сигнала.
n1=1:15;
cn=-1/j./n1/pi.*(cos(n1*pi)-1); // реализация расчета коэффициента Фурье
n2=-15:-1;
c_n=-1/j./n2/pi.*(cos(n2*pi)-1); //на разных интервалах
Cn=[c_n 0 cn];
n3=[n2 0 n1];
n=-15:15;
figure(1);
subplot(2,1,1);
stem(n,abs(Cn)); //построение графика амплитудного спектра сигнала
title('амплитудный спектр сигнала');
xlabel('количество гармоник');
subplot(2,1,2);
stem(n,angle(Cn)); //построение графика фазового спектра сигнала
title('фазовый спектр сигнала');
xlabel('число гармоник');
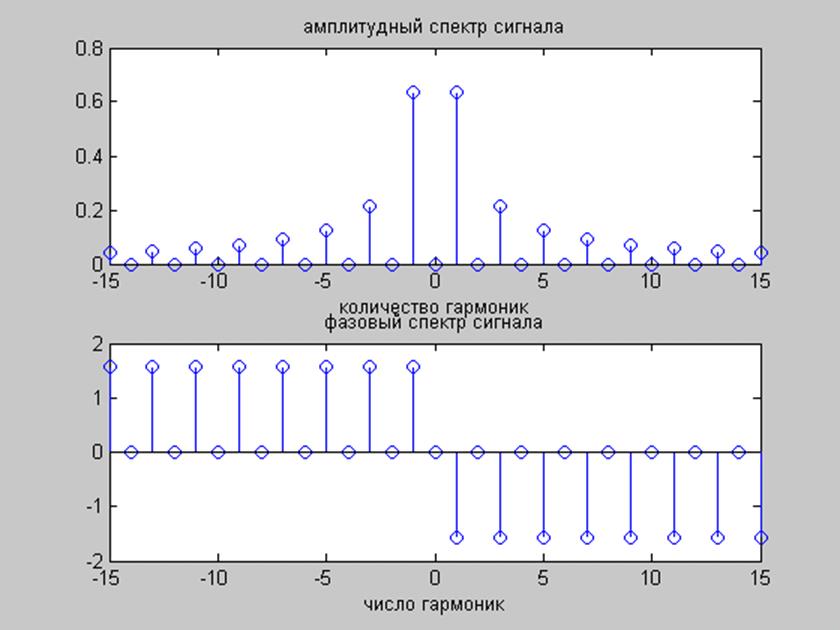
Задание 4.
Определить спектр Фурье сигнала с помощью функции fft(). Определить коэффициенты ряда Фурье для сигнала, заданного в п.2, с помощью fft(), построить графики амплитудного спектра.
T=20; // период сигнала
t=0:T/50:T; // временной интервал
x=1*rectpuls(t-5,10)-1*rectpuls(t-15,10); // генерирование сигнала
figure(1);
subplot(311), plot(t,x) // график сигнала
grid
title(' График сигнала')
k=0:50;
m=1:50
% коэффициенты ряда Фурье
C=1./j./m/pi.*(cos(pi*m)-1); // график амплитудного спектра
C1=[0 abs(C)];
subplot(312),
stem(2*pi*k/T, C1);
title(' Амплитудный спектр сигнала')
y=fft(x,51); //Дискретное преобразование Фурье сигнала
subplot(313), stem(2*pi*k/T, abs(y)/51)
xlabel(' Угловая частота, рад/сек')
title(' Амплитудный спектр сигнала по процедуре fft')
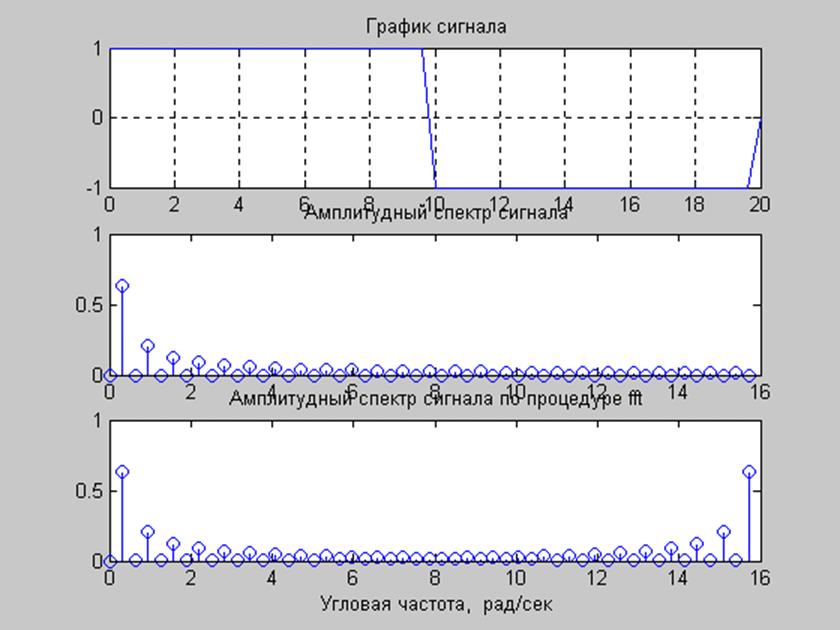
По данным графикам видно, что амплитудный спектр сигнала, построенный через процедуру расчета выведенных коэффициентов Cn и функции abs(Cn) , идентичен графику амплитудного спектра сигнала, построенного через процедуру fft() .
Задание 5.
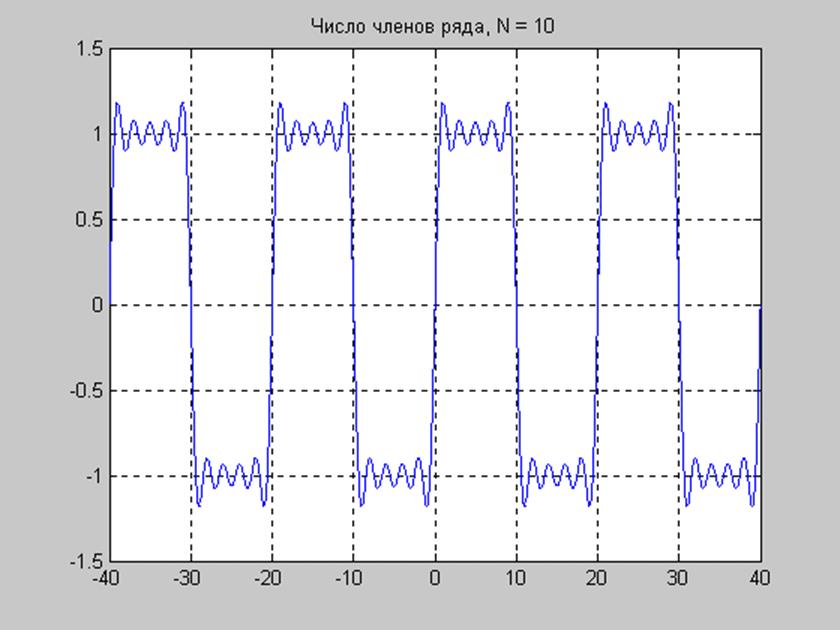
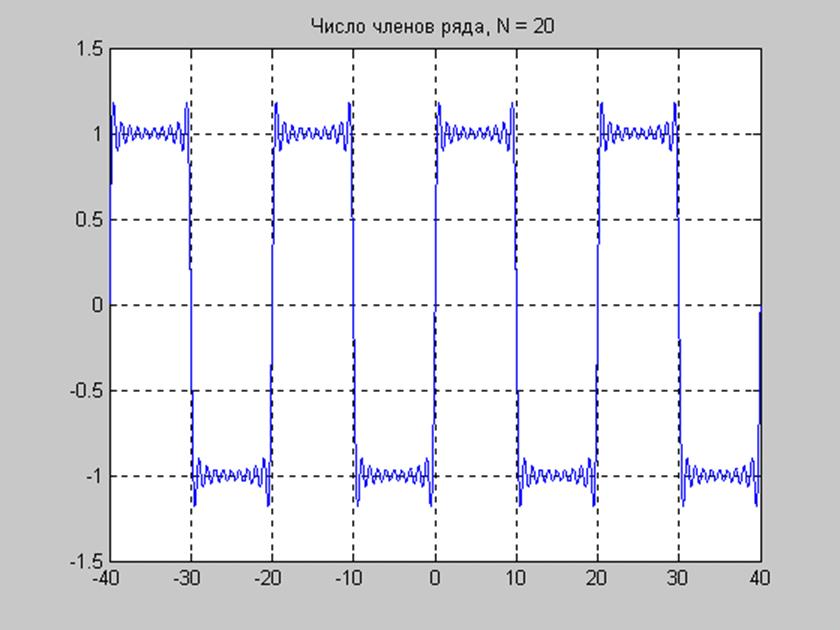
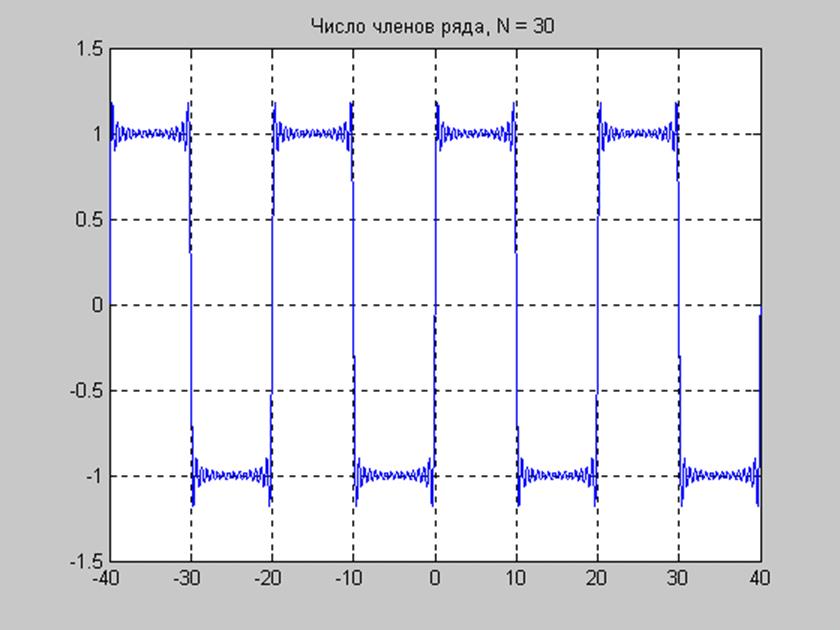
Составить и выполнить файл-сценарий для исследования сходимости ряда Фурье к исходному периодическому. Пронаблюдать сходимость ряда для четырех значений числа членов ряда и явление Гиббса.
T=20; // период сигнала
w0 = 2*pi/T; // циклическая частота
t = -2*T:T/1000:2*T;
N = input('Введите число членов ряда:');
c0 = 0;
x = c0*ones(1,length(t));
for n=1:N,
cn = -1/j./n/pi.*(cos(n*pi)-1); //коэффициенты ряда Фурье
c_n = conj(cn);
x = x + cn*exp(j*n*w0*t) + c_n*exp(-j*n*w0*t);
end
figure(2);
plot(t,x);
grid
title(['Число членов ряда, N = ',num2str(N)])
Явление Гиббса (увеличенный масштаб):
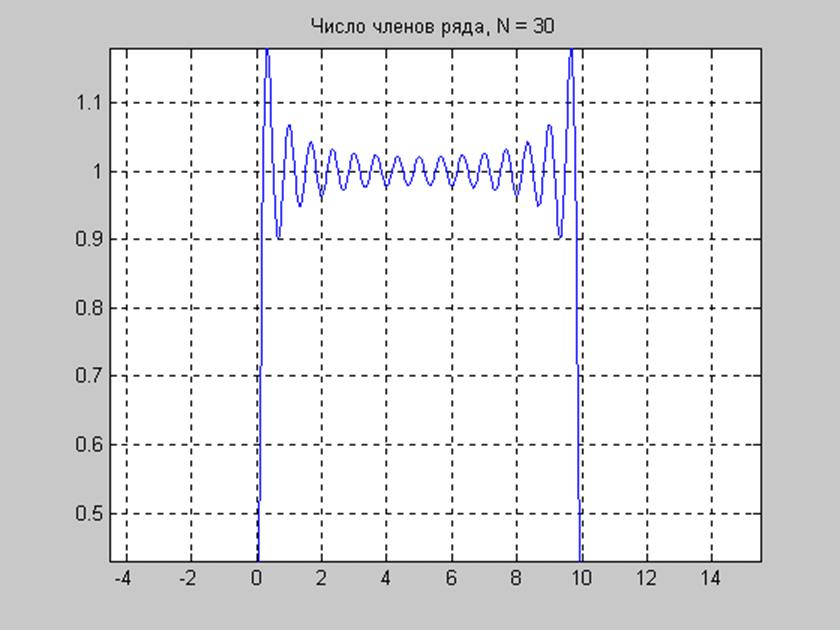
Из графиков видно, что ряд Фурье созданный на основе выведенных в п.2. коэффициентов приводит к исходному периодическому сигналу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.