НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 11
СЛУЧАЙНЫЕ СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ
Группа: АТ-33
Вариант: 1 Преподаватель:
Студент: Шадрина А.В. доц. Щетинин Ю.И.
2006
Цель работы: изучение основных характеристик стационарных случайных сигналов (среднего значения, автокорреляционной функции, спектральной плотности мощности) и приобретение практических навыков их вычисления и анализа в среде Matlab.
Выполнение работы:
1.
Генерирование случайного сигнала ![]() с нулевым математическим
ожиданием и единичной дисперсией с помощью функции
с нулевым математическим
ожиданием и единичной дисперсией с помощью функции ![]() . Вычисление
оценок среднего и дисперсии случайного сигнала.
. Вычисление
оценок среднего и дисперсии случайного сигнала.
![]() -
генерирование матрицы размером
-
генерирование матрицы размером ![]() из случайных
чисел, распределённых по нормальному закону с нулевым средним значением и
единичной дисперсией.
из случайных
чисел, распределённых по нормальному закону с нулевым средним значением и
единичной дисперсией.
>> X = randn(1,500);
>> stem(X)
>> title('Случайный сигнал N=500')
>> xlabel('n, номер отсчёта'), grid
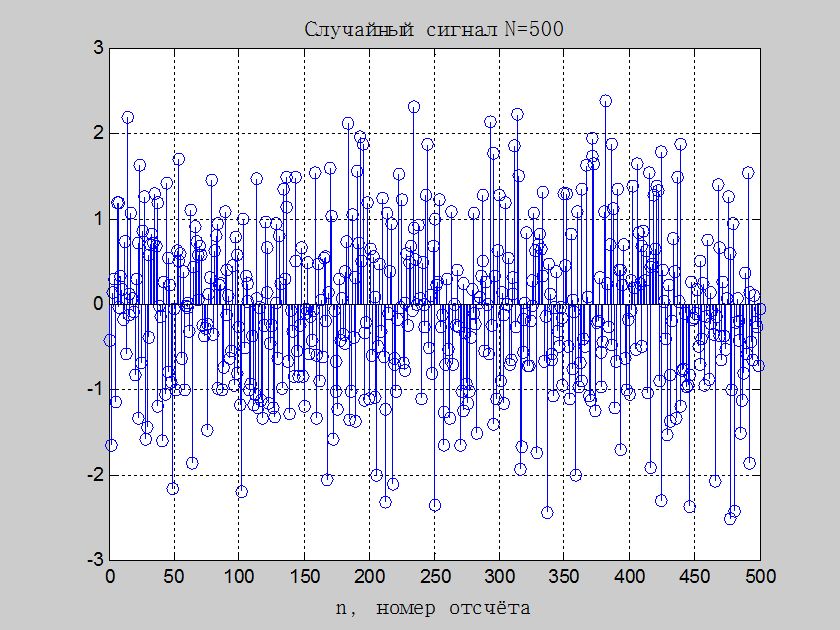
Рис.1. График случайного сигнала с нулевым математическим ожиданием и единичной дисперсией
Оценки среднего и дисперсии
сигнала по независимым наблюдениям ![]() определяются как
определяются как
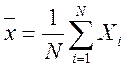 ,
,
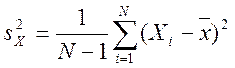 .
.
Matlab function (estimate.m)
function [m,D] = estimate(X)
N = length(X);
sum1 = 0;
for i = 1:N
sum1 = sum1+X(i);
end
m = sum1/N;
sum2 = 0;
for i = 1:N
sum2 = sum2+(X(i)-m).^2;
end
D = sum2/(N-1);
>> [m,D] = estimate(X)
m =
-0.06294046047724
D =
0.89628824900700
>> M = mean(X) %оценка среднего
M =
-0.06294046047724
>> D = var(X) %оценка дисперсии
D =
0.89628824900700
Комментарий: Главными
характеристиками любого случайного процесса являются его законы распределения.
Они являются наиболее полными. В данном пункте был сгенерирован случайный
сигнал, распределенный по нормальному закону. Чаще всего на практике вместо
закона распределения (функции распределения или плотности распределения)
ограничиваются менее полными характеристиками – математическим ожиданием,
дисперсией. Здесь - математическое ожидание равно нулю, а дисперсия - единице.
Но! эти значения являются идеализированными, т.е. применимы только для сигналов
бесконечной длительности. Здесь же - число отсчётов, для которых определяются
значения случайного сигнала, конечно и равно 500. Вследствие данного опыта
получается иная реализация случайного процесса, отличная от теоретической,
поэтому значения среднего и дисперсии не совпадают с заданными. Среднее
отличается от теоретического значения на 0,0629, а дисперсия – на 0,1037. Если
увеличивать количество отсчётов случайного сигнала, т.е. устремлять ![]() , то эти характеристики будут
отличаться от теоретических всё меньше и меньше.
, то эти характеристики будут
отличаться от теоретических всё меньше и меньше.
2.
График плотности вероятности нормальной случайной величины из
п.1 и график гистограммы сигнала с помощью функции ![]() с
числом интервалов
с
числом интервалов ![]() .
.
![]() - хранит элементы
- хранит элементы ![]() в
в ![]() равных
интервалах и возвращает число элементов в каждом интервале.
равных
интервалах и возвращает число элементов в каждом интервале.
>> x = -5:0.1:5;
>> f = 1/sqrt(2*pi*var(X))*exp(-(x-mean(X)).^2/2/var(X));
>> subplot(2,1,1)
>> plot(x,f)
>> title('График плотности вероятности нормальной случайной величины')
>> subplot(2,1,2)
>> hist(X,20)
>> title('График гистограммы нормального случайного сигнала')
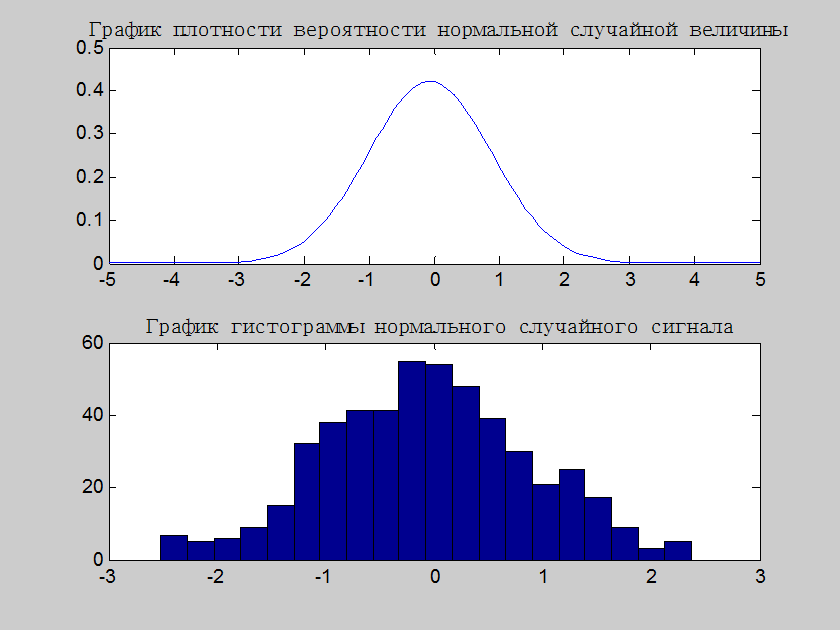
Рис.2. Графики плотности вероятности и гистограммы нормальной случайной величины из п.1
Комментарий: Плотность
вероятности при нормальном законе распределения описывается функцией 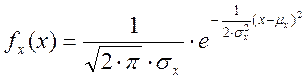 при
при ![]() .
Плотность вероятности показывает – какова вероятность встретить определённое
значение случайного сигнала. Из рис.2 видно, что наиболее вероятно появление
значений близких к нулю, что соответствует значению среднего
.
Плотность вероятности показывает – какова вероятность встретить определённое
значение случайного сигнала. Из рис.2 видно, что наиболее вероятно появление
значений близких к нулю, что соответствует значению среднего ![]() . Вероятность встретить эти значения
около 0,42 или 42%. Если обратиться к рис.1, то можно заметить, что значения
случайного сигнала большие 3-х отсутствуют, что подтверждается графиком
плотности распределения, т.к. плотность распределения при значениях больше 3-х
равна нулю. Площадь под кривой плотности вероятности равна единице, т.е.
. Вероятность встретить эти значения
около 0,42 или 42%. Если обратиться к рис.1, то можно заметить, что значения
случайного сигнала большие 3-х отсутствуют, что подтверждается графиком
плотности распределения, т.к. плотность распределения при значениях больше 3-х
равна нулю. Площадь под кривой плотности вероятности равна единице, т.е. 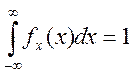 (условие нормировки). Т.о. меняя
пределы интегрирования можно узнать – какова вероятность попадания значения
сигнала в определённый интервал. При большом объёме выборки её элементы
объединяются в группы, представляя результаты опытов в виде группированного
статистического ряда (анализируется частота встречаемости значений сигнала из
интервала). График гистограммы отражает суть вышесказанного. Здесь интервал,
содержащий все элементы выборки, разбивается на 20 одинаковых интервалов и
подсчитывается общее число значений случайного сигнала, попавших в этот
интервал. Т.о. видно, что больше всего значений случайного сигнала
сосредоточено около нуля (55 слева и 54 справа), а меньше всего около 2-х (3
значения). Сумма всех значений гистограммы даёт длину выборки, т.е. 500.
(условие нормировки). Т.о. меняя
пределы интегрирования можно узнать – какова вероятность попадания значения
сигнала в определённый интервал. При большом объёме выборки её элементы
объединяются в группы, представляя результаты опытов в виде группированного
статистического ряда (анализируется частота встречаемости значений сигнала из
интервала). График гистограммы отражает суть вышесказанного. Здесь интервал,
содержащий все элементы выборки, разбивается на 20 одинаковых интервалов и
подсчитывается общее число значений случайного сигнала, попавших в этот
интервал. Т.о. видно, что больше всего значений случайного сигнала
сосредоточено около нуля (55 слева и 54 справа), а меньше всего около 2-х (3
значения). Сумма всех значений гистограммы даёт длину выборки, т.е. 500.
3.
Автокорреляционная функция (АКФ) случайного дискретного сигнала.
Определение АКФ выходного сигнала для системы с уравнением ![]() при входном сигнале в виде
белого шума с АКФ. Определение той же функции с использованием процедуры
при входном сигнале в виде
белого шума с АКФ. Определение той же функции с использованием процедуры ![]() , в качестве входа рассматривается случайный
процесс из п.1. График
, в качестве входа рассматривается случайный
процесс из п.1. График ![]() .
.
Для случайного дискретного
процесса автокорреляционная функция определяется выражением: ![]() . То есть АКФ вычисляется с
использованием операции усреднения произведений значений случайного сигнала,
отстоящих друг от друга на m отсчетов. АКФ
определяет насколько сильна связь между отсчетами сигнала, разделенными друг от
друга интервалом m. Любой реальный процесс имеет
конечную память, поэтому для таких сигналов с увеличением интервала m между отсчетами степень
связи должна ослабевать.
. То есть АКФ вычисляется с
использованием операции усреднения произведений значений случайного сигнала,
отстоящих друг от друга на m отсчетов. АКФ
определяет насколько сильна связь между отсчетами сигнала, разделенными друг от
друга интервалом m. Любой реальный процесс имеет
конечную память, поэтому для таких сигналов с увеличением интервала m между отсчетами степень
связи должна ослабевать.
Выражение связи между АКФ выходного
![]() и входного сигналов
и входного сигналов ![]() линейной дискретной системы:
линейной дискретной системы: ![]() , где
, где ![]() -
импульсная характеристика. В данном случае входной сигнал представляет собой
белый шум с АКФ
-
импульсная характеристика. В данном случае входной сигнал представляет собой
белый шум с АКФ ![]() , при этом
, при этом ![]() - дисперсия шума,
- дисперсия шума, ![]() - единичный дельта-импульс.
- единичный дельта-импульс.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.