Уравнение системы имеет вид
![]() .
.
Импульсная характеристика системы (реакция дискретной системы на входной сигнал в виде единичного дельта-импульса при нулевых начальных условиях):
![]() .
.
Выражение связи между АКФ выходного и входного сигналов данной ЛДС:
![]() .
.
Свёртка 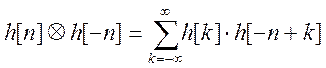 или
или
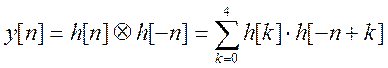 , где
, где ![]() и
и
![]()
![]()
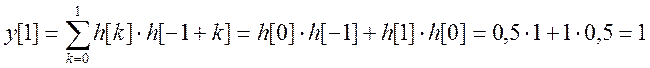

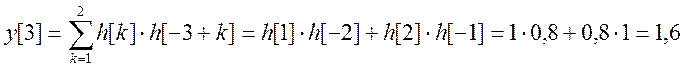
![]()
Т.о. ![]() .
.
АКФ выходного сигнала: ![]() . Если в качестве входного сигнала
использовать сигнал из п.1, у которого дисперсия равна 0,8962, то т.о. АКФ
выходного сигнала:
. Если в качестве входного сигнала
использовать сигнал из п.1, у которого дисперсия равна 0,8962, то т.о. АКФ
выходного сигнала: ![]() .
.
Matlab script (labrab111.m)
h1 = [0.5 1 0.8];
h2 = [0.5 1 0.8];
y1 = conv(h1,h2)
Kx = var(X);
Ky = conv(y1,Kx)
stem(Ky)
title('АКФ выходного сигнала')
xlabel('n, отсчёт'), grid
>> y1 = 0.25 1 1.80 1.60 0.64
Ky = 0.2241 0.8963 1.6133 1.4345 0.5736
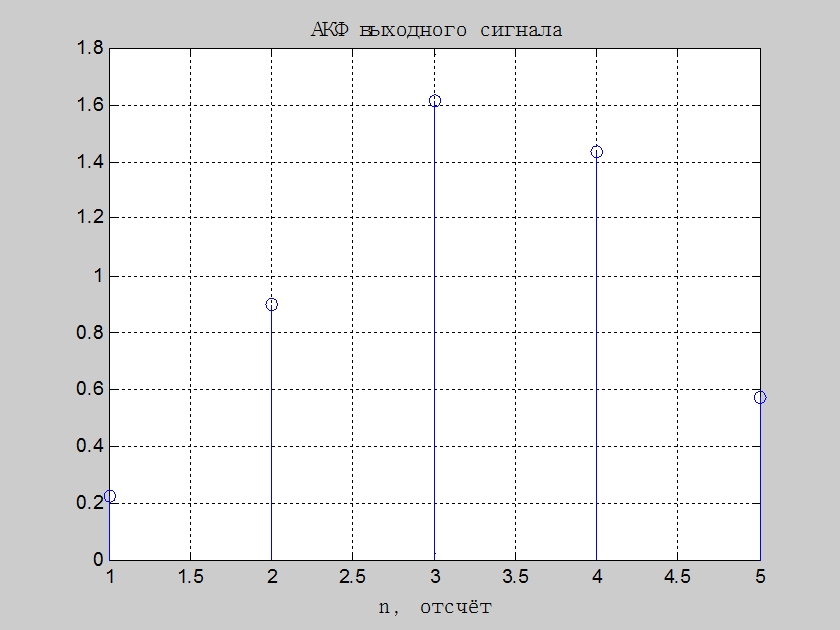
Рис.3. Автокорреляционная
функция выходного сигнала для дискретной системы ![]() при
входном сигнале в виде белого шума из п.1
при
входном сигнале в виде белого шума из п.1
Комментарий: Входной
сигнал системы является белым шумом. Для такого сигнала значения Xn и Xn+m некоррелированны для любого ![]() , то есть не зависят друг от друга.
АКФ входного сигнала имеет вид
, то есть не зависят друг от друга.
АКФ входного сигнала имеет вид ![]() , т.е. входной сигнал
определяется только данным моментом времени. Для выходного сигнала системы АКФ
определяется сверткой вида
, т.е. входной сигнал
определяется только данным моментом времени. Для выходного сигнала системы АКФ
определяется сверткой вида ![]() . При этом
посредством так называемого формирующего фильтра входной некоррелированный
сигнал (белый шум) преобразуется в выходной коррелированный сигнал (окрашенный
шум). С ростом m связь ослабевает, поэтому
значения АКФ уменьшаются.
. При этом
посредством так называемого формирующего фильтра входной некоррелированный
сигнал (белый шум) преобразуется в выходной коррелированный сигнал (окрашенный
шум). С ростом m связь ослабевает, поэтому
значения АКФ уменьшаются.
4.
Генерирование случайного сигнала ![]() длительностью
1000 отсчетов, распределенного по нормальному закону с нулевым средним
значением и единичной дисперсией. Вычисление выходного сигнал
длительностью
1000 отсчетов, распределенного по нормальному закону с нулевым средним
значением и единичной дисперсией. Вычисление выходного сигнал ![]() для системы с уравнением
для системы с уравнением ![]() . Графики рассеяния для
четырех случаев:
. Графики рассеяния для
четырех случаев:
а. (Yi, Yi+1),
б. (Yi, Yi+2),
в. (Yi, Yi+3),
г. (Yi, Yi+4) (i =1, 2… 900).
Степень
коррелированности значений случайного сигнала ![]() .
.
Matlab script (labrab112.m)
N = 1000;
X = randn(1,N);
n = 1:1000;
num = [0.5 1 0.8];
den = [1];
Y(n) = filter(num,den,X);
i = 1:900;
Y0(i) = Y(i);
Y1(i) = Y(i+1);
Y2(i) = Y(i+2);
Y3(i) = Y(i+3);
Y4(i) = Y(i+4);
subplot(4,1,1), plot(Y0,Y1,'.'), title('График рассеяния Yi,Yi+1')
subplot(4,1,2), plot(Y0,Y2,'.'), title('График рассеяния Yi,Yi+2')
subplot(4,1,3), plot(Y0,Y3,'.'), title('График рассеяния Yi,Yi+3')
subplot(4,1,4), plot(Y0,Y4,'.'), title('График рассеяния Yi,Yi+4')
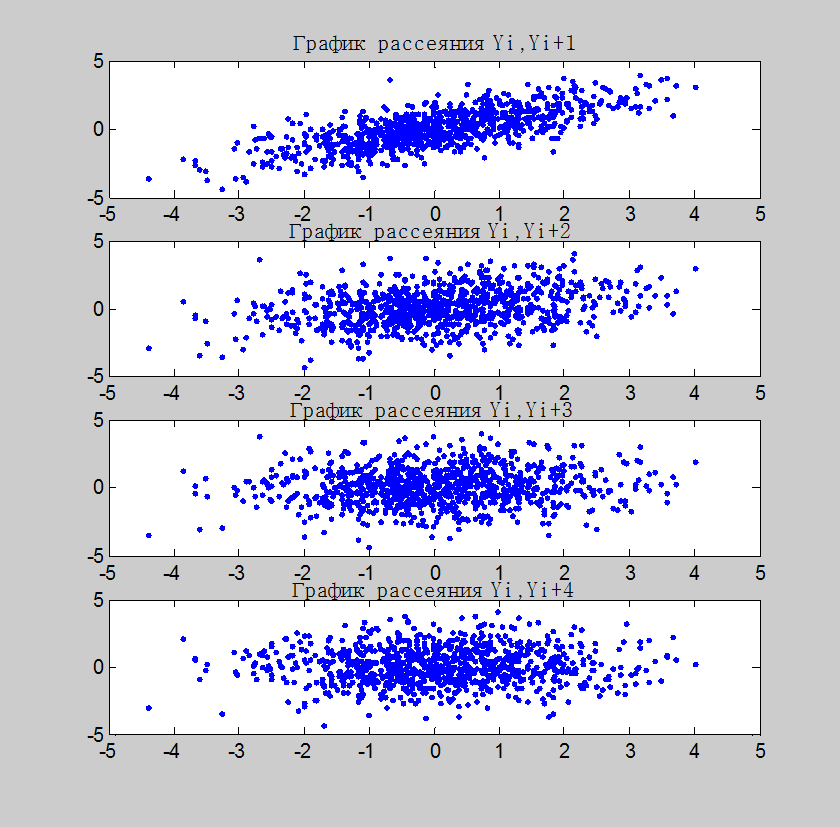
Рис.4.
Графики рассеяния для случаев (Yi,
Yi+1), (Yi, Yi+2),
(Yi, Yi+3),
(Yi, Yi+4),
где Yi – сигнал
на выходе фильтра с уравнением ![]() при входном
сигнале в виде белого шума
при входном
сигнале в виде белого шума
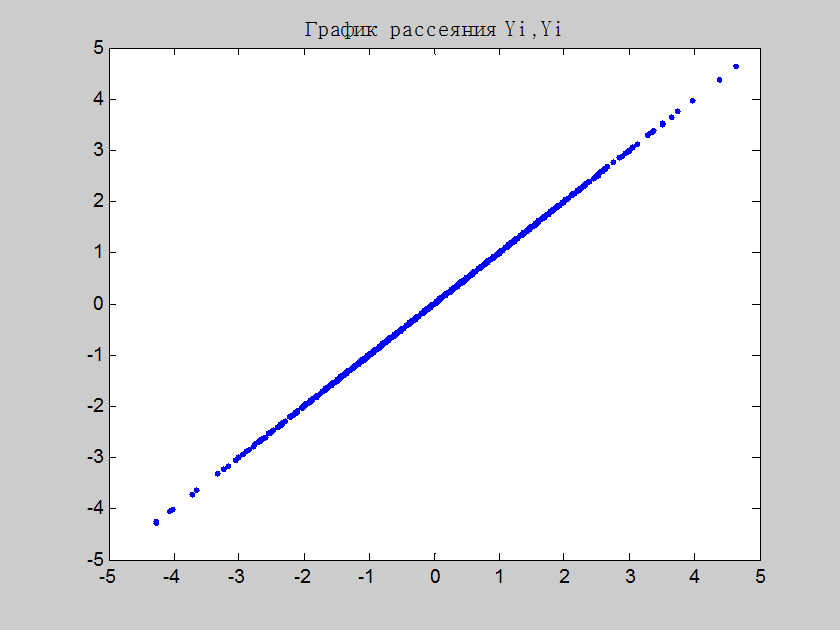
Рис.5. Графики рассеяния для случая (Yi, Yi)
Комментарий: На рис.4 представлены графики рассеяния значений Yi+m относительно значений Yi, а на рис.5 представлен график рассеяния Yi относительно самого себя. Т.е. для коррелированных значений график рассеяния должен иметь вид прямой линии. Если обратиться к рис.4, то нетрудно заметить, что представленные графики далеки от линейного вида. С ростом увеличения интервала m отклонение от линейности всё более возрастает. На графике рассеяния Yi+1 относительно Yi ещё прослеживается некоторое подобие линейности, т.е. из всех представленных случаев Yi+1 будет сильнее остальных коррелирован с Yi, таким образом, зная значение Yi можно предугадать и среднее значение Yi+1. Иначе дело обстоит для Yi, Yi+4 – эти значения слабо коррелированны и здесь сложно давать оценку среднему значению Yi+4, полагаясь исключительно на значение Yi.
5.
Определение оценки автокорреляционной функции выходного сигнала
при входном сигнале из п.1 с использованием функции ![]() .
Графики АКФ. Определение взаимной корреляционной функции выходного и входного
сигналов фильтра.
.
Графики АКФ. Определение взаимной корреляционной функции выходного и входного
сигналов фильтра.
![]() -
возвращает нормализованный вектор АКФ сигнала в соответствии с
-
возвращает нормализованный вектор АКФ сигнала в соответствии с ![]() .
.
Matlab script (labrab113.m)
m = -499:499;
n = -501:501;
Xc = xcorr(X,'biased');
delta = (m==0);
Kx = var(X)*delta;
h1 = [0.5 1 0.8];
h2 = [0.5 1 0.8];
y1 = conv(h1,h2);
Kyy1 = conv(Kx,y1);
Kyy2 = conv(Xc,y1);
subplot(2,1,1), stem(n,Kyy1), grid
title('АКФ выходного сигнала фильтра (аналитический расчёт)')
xlabel('n, отсчёт')
axis([-40 40 -0.5 2])
subplot(2,1,2), stem(n,Kyy2), grid
axis([-40 40 -0.5 2])
title('Смещённая оценка АКФ выходного сигнала фильтра')
xlabel('n, отсчёт')
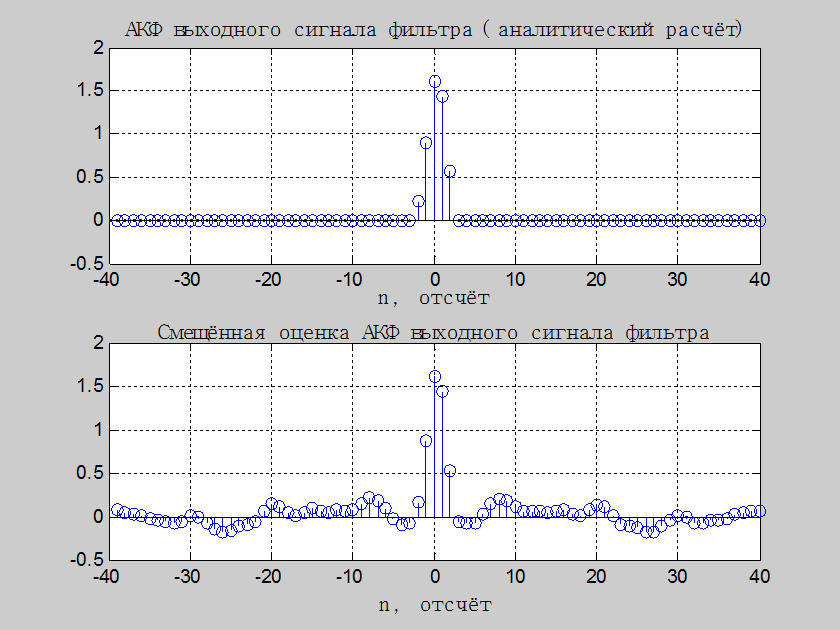
Рис.6. Графики АКФ и
смещённой оценки АКФ выходного сигнала фильтра с уравнением ![]() при входном сигнале из п.1
при входном сигнале из п.1
Комментарий: Различия
в графиках наблюдаются по той причине, что в первом случае при аналитическом
расчёте значение АКФ входного сигнала бралось для «идеального» белого шума,
т.е. ![]() -
некоррелированный входной сигнал, где количество отсчётов этого случайного
сигнала бесконечно, а во втором случае входным сигналом системы являлся белый
шум, но определённый только для конечного числа отсчётов, вследствие конечной
длины сигнала возникает погрешность (значения сигнала мало, но всё-таки,
коррелированны между собой), которую можно наблюдать на рис.6. Если увеличивать
число отсчётов, то второй график всё более будет приближаться к виду первого
графика.
-
некоррелированный входной сигнал, где количество отсчётов этого случайного
сигнала бесконечно, а во втором случае входным сигналом системы являлся белый
шум, но определённый только для конечного числа отсчётов, вследствие конечной
длины сигнала возникает погрешность (значения сигнала мало, но всё-таки,
коррелированны между собой), которую можно наблюдать на рис.6. Если увеличивать
число отсчётов, то второй график всё более будет приближаться к виду первого
графика.
Matlab script (labrab114.m)
n = -499:499;
num = [0.5 1 0.8];
den = [1];
Y = filter(num,den,X);
K = xcorr(Y,X);
stem(n,K)
title('Взаимная корреляционная функция входного и выходного сигналов')
xlabel('n, отсчёт'), grid
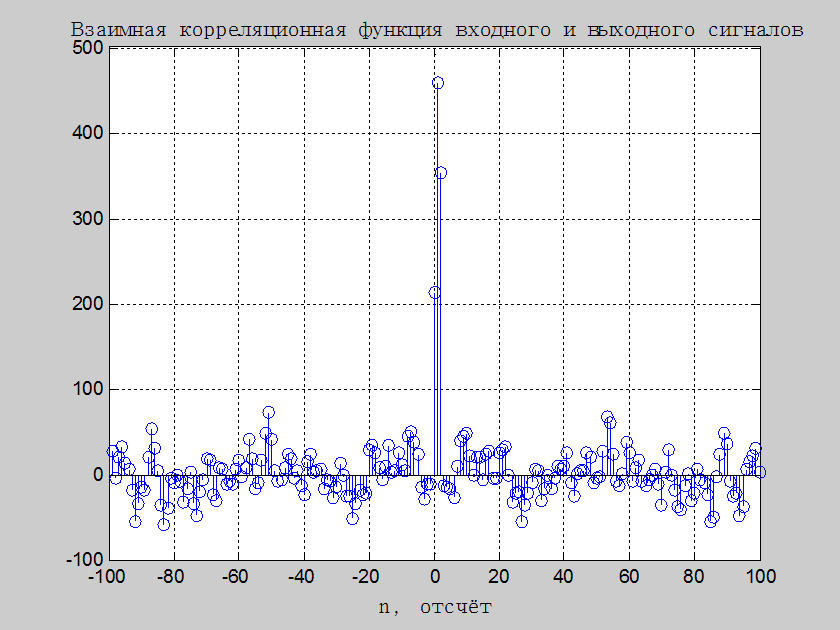
Рис.7. Взаимная
корреляционная функция входного сигнала из п.1 и сигнала на выходе фильтра с
уравнением ![]()
Комментарий: Часто
требуется совместно рассматривать несколько случайных сигналов. К таким задачам
относится исследование входного и выходного сигналов системы. Характеристикой
связи двух случайных сигналов X(t) и Y(t) является их взаимная корреляционная функция ![]() . Из графика, представленного на
рис.7 видно, что выходной сигнал системы очень сильно зависит от значений
входного сигнала, определённых в данный момент времени - ноль, в предыдущий –
единица и идущий пред предыдущим – двойка. При чём сильнее всего зависит от
значения, определённого в предыдущий момент времени и менее всего – в данный
момент времени. Очень слабая зависимость идёт в остальные моменты времени, хотя
если обратиться к уравнению фильтра
. Из графика, представленного на
рис.7 видно, что выходной сигнал системы очень сильно зависит от значений
входного сигнала, определённых в данный момент времени - ноль, в предыдущий –
единица и идущий пред предыдущим – двойка. При чём сильнее всего зависит от
значения, определённого в предыдущий момент времени и менее всего – в данный
момент времени. Очень слабая зависимость идёт в остальные моменты времени, хотя
если обратиться к уравнению фильтра ![]() , то в идеале график
ВКФ должен представлять из себя три единичных импульса в моменты времени 0, 1 и
2, но т.к. здесь опять же входной сигнал является выборкой конечной длины, то
соответственно появляется погрешность.
, то в идеале график
ВКФ должен представлять из себя три единичных импульса в моменты времени 0, 1 и
2, но т.к. здесь опять же входной сигнал является выборкой конечной длины, то
соответственно появляется погрешность.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.