6. Свойство (теорема) свертки.
Если последовательности ![]() и
и ![]() имеют
дискретные преобразования Фурье
имеют
дискретные преобразования Фурье ![]() и
и ![]() , то последовательность
, то последовательность ![]() вида
вида
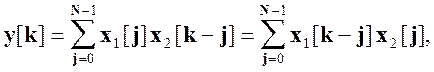 (5.32)
(5.32)
будет иметь ДПФ ![]() , заданное выражением
, заданное выражением
![]() (5.33)
(5.33)
т.е. дискретной свертке во временной области соответствует произведение ДПФ умноженное на N.
В дальнейшем дискретную свёртку будем обозначать также символом Ä.
Доказательство. Запишем ДПФ для y[k]
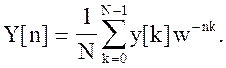 (5.34)
(5.34)
Выразим y[k] через свертку и изменим порядок суммирования, тогда
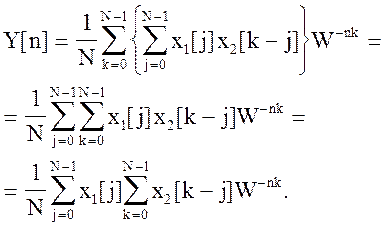 (5.35)
(5.35)
Обозначим k - j = m, при этом k = j + m. Следовательно,
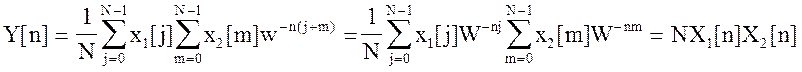 (5.36)
(5.36)
Свойство свертки особенно широко используется в задачах цифровой обработки сигналов , линейной фильтрации, анализе временных рядов.
Рассмотренные свойства показывают, что многие из средств обычного непрерывного преобразования Фурье применимы к ДПФ. Однако некоторые из свойств не выполняются для ДПФ, а другие видоизменяются из-за периодичности дискретных преобразований. В таблице 5.1 приведена сводка основных свойств ДПФ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.