Информатика и выч. техника \ Теория и обработка сигналов

Изучение понятия и свойств непрерывной и дискретной свертки. Вариант 4, страница 2

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Дельта - функция, дополненная нулями справа'); grid;

subplot(313), stem((0:length(con)-1),con); grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Свертка прямоугольной волны и дельта - функции, дополненной нулями справа');

axis([0 (length(con)-1) 1.2*min(con) 1.2*max(con)]);

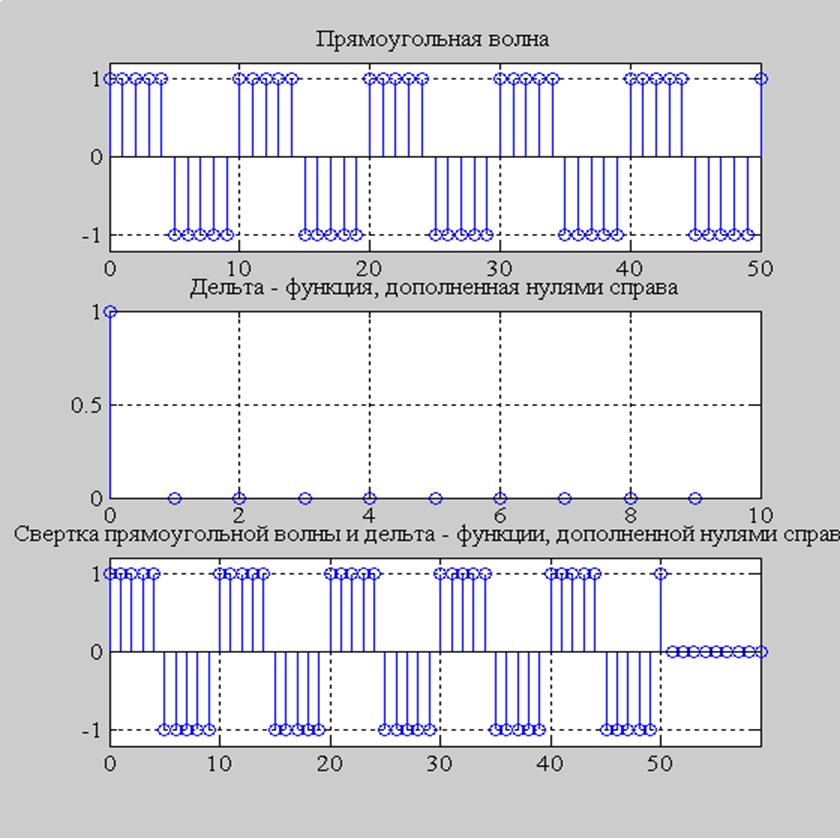
Рис. 4.  Графики прямоугольной волны, дельта-функции, дополненной нулями справа, свертка прямоугольной волны и дельта-функции, дополненной нулями справа.

Комментарий:

Из рисунков 3 и 4  видно, свертка в пунктах 4 и 5 различается длиной и последними отсчетами. Это объясняется геометрическим смыслом свертки (при сдвиге прямоугольного сигнала через дельта-функцию, дополненную нулями, последние отсчеты получаются нулевыми, т.к. прямоугольный сигнал умножается на нули, которыми была дополнена дельта-функцию).

6. Вычисление свертки плоской и прямоугольной последовательности импульсов.

Ниже приведен код программы, с помощью которого были построение графики и произведены вычисления:

h1=[ones(1,3)];

h2=[ones(1,10)];

T=10;

sq=sqgen(50, T);

con1=conv(h1,sq);

con2=conv(h2,sq);

subplot(211), stem((0:length(con1)-1), con1); grid

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Свертка прямоугольной волны и плоской, длительностью 3');

axis([0 length(con1) 1.2*min(con1) 1.2*max(con1)]);

subplot(212), stem((0:length(con2)-1), con2); grid

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Свертка прямоугольной волны и плоской, длительностью 10');

axis([0 length(con2) 1.2*min(con2) 1.2*max(con2)]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

disp('Свертка 1 длина = ');disp(length(con1));

disp('Свертка 2 длина = ');disp(length(con2));

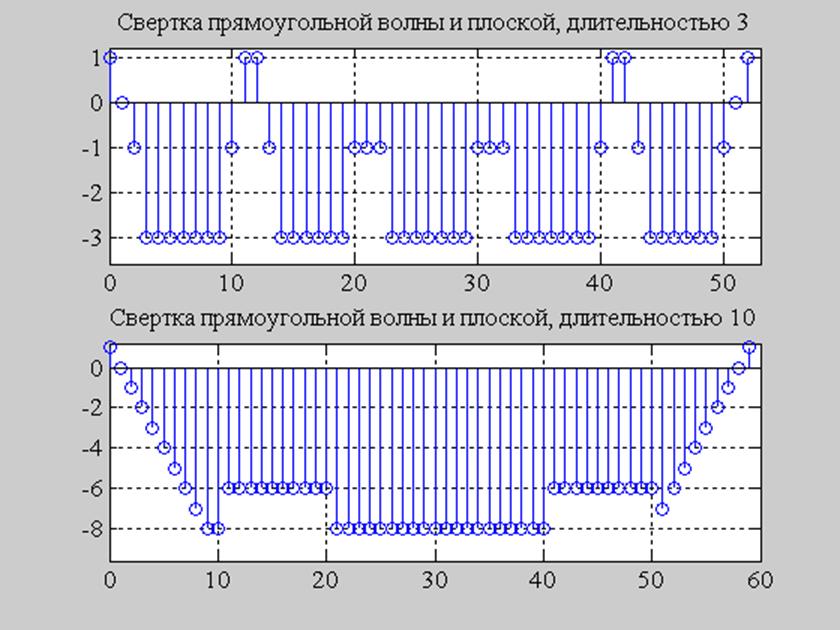
Рис. 5. Графики свертки плоского импульса и прямоугольной волны, с различными длинами плоского импульса (сверху вниз) длина 3 отчета; длина 10 отчетов.

Свертка 1 длина =

    53

Свертка 2 длина =

    60

7. Построение графиков сигналов х1 и х2, свертки этих сигналов и восстановление сигнала х1 из свертки сигналов х1 и х2.

Аналитическое выражение сигналов:

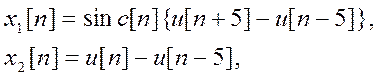
где 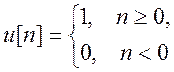     - дискретная единичная ступенчатая функция.

n=-5:5;

x1=sinc(n/pi);

x2=[1 1 1 1 1];

con=conv(x1,x2);

decon=deconv(con,x2);

subplot(411), stem (n,x1); grid

axis([min(n) max(n)  1.4*min(x1) 1.2*max(x1)]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Сигнал x1');

subplot(412), stem ((0:length(x2)-1),x2); grid

axis([ 0 (length(x2)-1) 0 1.2*max(x2)]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Сигнал x2');

subplot(413), stem ((0:length(con)-1),con); grid

axis([ 0 (length(con)-1) 1.4*min(con) 1.2*max(con)]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Свертка сигналов х1 и х2');

subplot(414), stem (n,decon); grid

axis([min(n) max(n) 1.4*min(decon) 1.2*max(decon)]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Восстановленный x1');

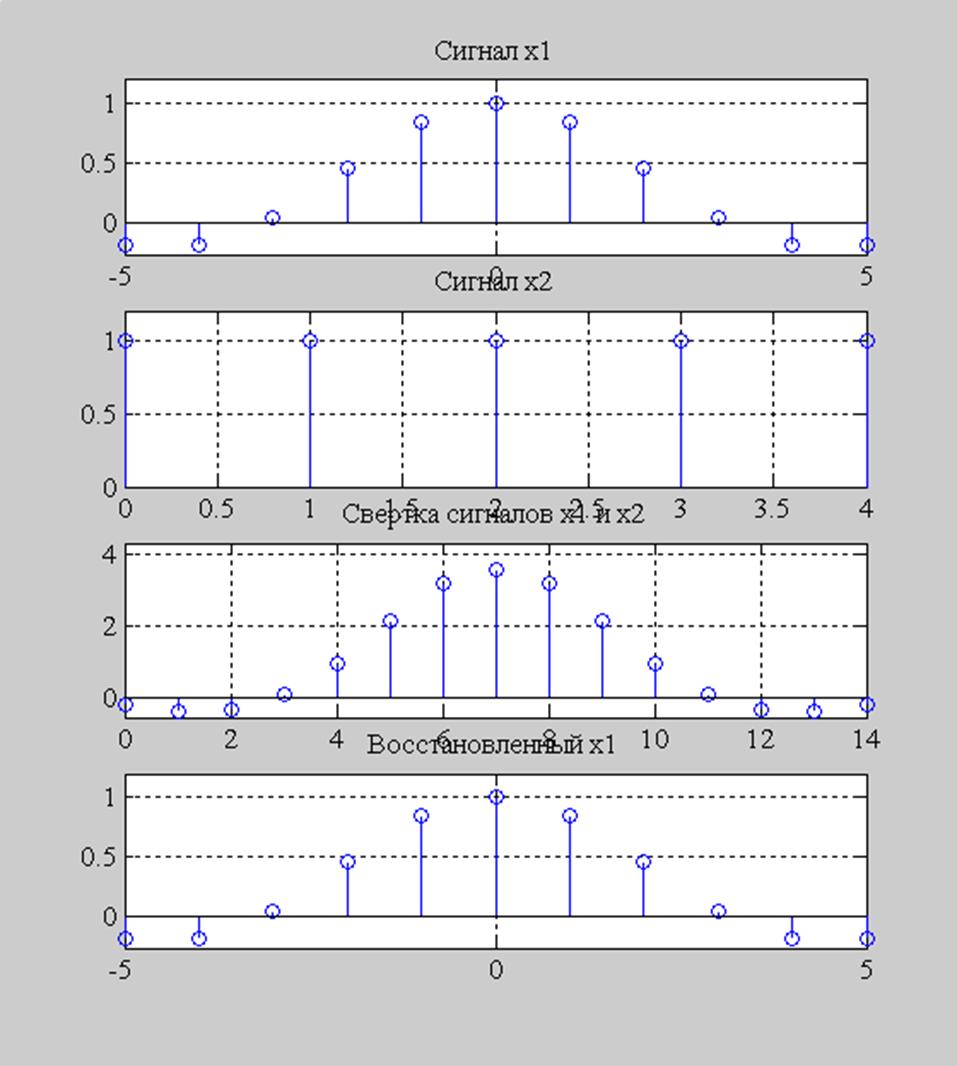
Рис. 6. Графики сигнала х1; сигнала х2; свертки сигналов х1и х2; восстановленного сигнала х1 из сверки.

8.  Вычисление свертки во временной области и в частотной при этом определение времени необходимого на эти операции.

Ниже приведен код программы, с помощью которого были построены свертки с помощью функции conv()  и с помощью функций fft() и ifft().

            % Вычисление свертки во временной области и в частотной

i=0:100;

a=0.05;

x1=exp(-a*i);           % сигнал  x1

x2=rectpuls(i-20,40);   % сигнал  x2

x1z=[x1 zeros(1,256-length(x1))];

x2z=[x2 zeros(1,256-length(x2))];

t1=cputime;

for n=0:999,

    con=(T*conv(x1,x2));

end

t1=(cputime-t1)

t1=cputime;

for n=0:999,

    conf=ifft(fft(x1z).*fft(x2z));

end

t2=(cputime-t1)

subplot(211), plot((0:length(con)-1),conv(x1,x2)); grid

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Свертка, вычисленная с помощью функции conv')

subplot(212), plot((0:length(conf)-1),abs(conf)); grid

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Свертка, вычисленная с помощью функции fft и ifft')

axis([00 (length(con)-1) 1.2*min(conf) 1.2*max(conf)]);

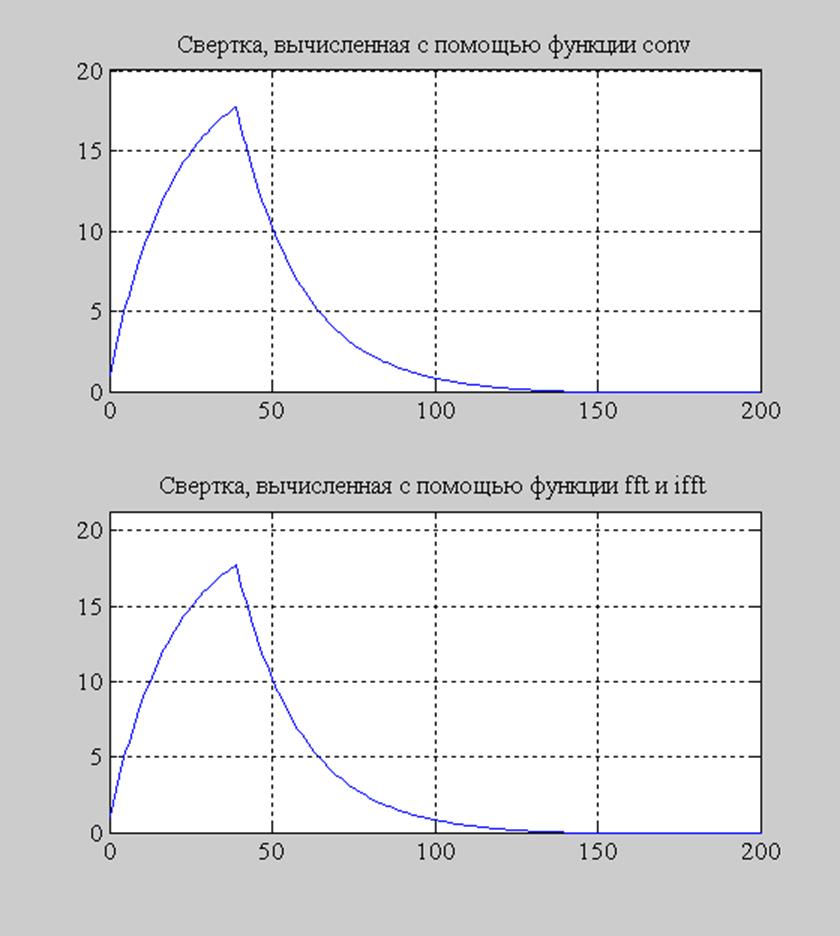
Рис. 7.  Графики сверток, построенных с помощью функций: (сверху вниз) conv();  fft() и ifft().

t2 =

    0.0780

t2 =

    0.0310

Время, которое понадобилось на вычисление свертки во временной области 78 мс, в частотной области (круговая свертка)  31мс, т.е. в 2 раза быстрей.

Вывод:

1) Сверткой двух функций называется интеграл вида

 

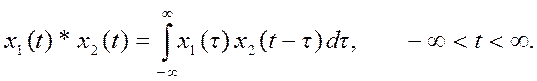
Численное вычисление непрерывной свертки может быть аппроксимировано конечной суммой вида
                   ,

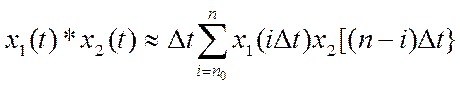где   - интервал (шаг) дискретизации.

2) Свойство свертки заключается в том, что свертке двух функций во временной области соответствует произведение их преобразований Фурье в частотной области.

3) Если  один из сигналов, участвующих в свертке, представляет собой дельта-функцию, то эта свертка в точности повторяет другой сигнал. В реальных системах сигнал не может представлять собой дельта-функцию, т.к. амплитудный спектр дельта-функции является прямой линией на любой частоте, а это не может быть достигнуто в реальной системе.

 При сдвиге прямоугольного сигнала через дельта-функцию, дополненную нулями, последние отсчеты получаются нулевыми, т.к. прямоугольный сигнал умножается на нули, которыми была дополнена дельта-функцию. 

Скачать файл