МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
ЛАБОРАТОРНАЯ РАБОТА № 5
НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ СВЕРТКИ
Группа: АИ-72 Преподаватель: доц. Щетинин Ю.И.
Выполнил: Пушкарева Ю.
Новосибирск
2009
Цель работы: изучение понятия и свойств непрерывной и дискретной свертки, приобретение практических навыков вычисления свертки в среде Matlab.
1. Вычисление непрерывной свертки сигнала прямоугольной формы и экспоненциального сигнала.
Свертка двух непрерывных по
времени сигналов определяется выражением
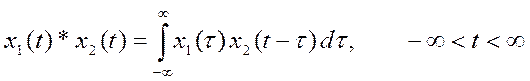 (1)
(1)
Численное вычисление непрерывной
свертки может быть аппроксимировано конечной суммой вида
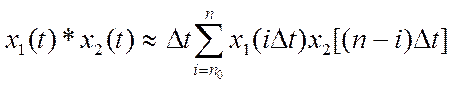 ,
(2)
,
(2)
где ![]() - интервал дискретизации.
- интервал дискретизации.
С помощью
следующего script-файла вычислим непрерывную свёртку
сигнала прямоугольной формы и экспоненциального сигнала по выражению (2) и с
помощью функции ![]() Matlab,
а также построим графики сигналов и их свёртки.
Matlab,
а также построим графики сигналов и их свёртки.
T=0.0001;
t=0:0.0001:0.1;
x1=5*rectpuls(t-0.03,0.02); % сигнал x1
t1 = 0:0.0001:0.05;
x2 =[100*t1 zeros(1,length(t1)-1)]; % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(t,x1), title('x1')
subplot(412), plot(t,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y),title('Свертка x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
title('Вычисление с помощью conv')
Полученные результаты представлены на рис. 1.
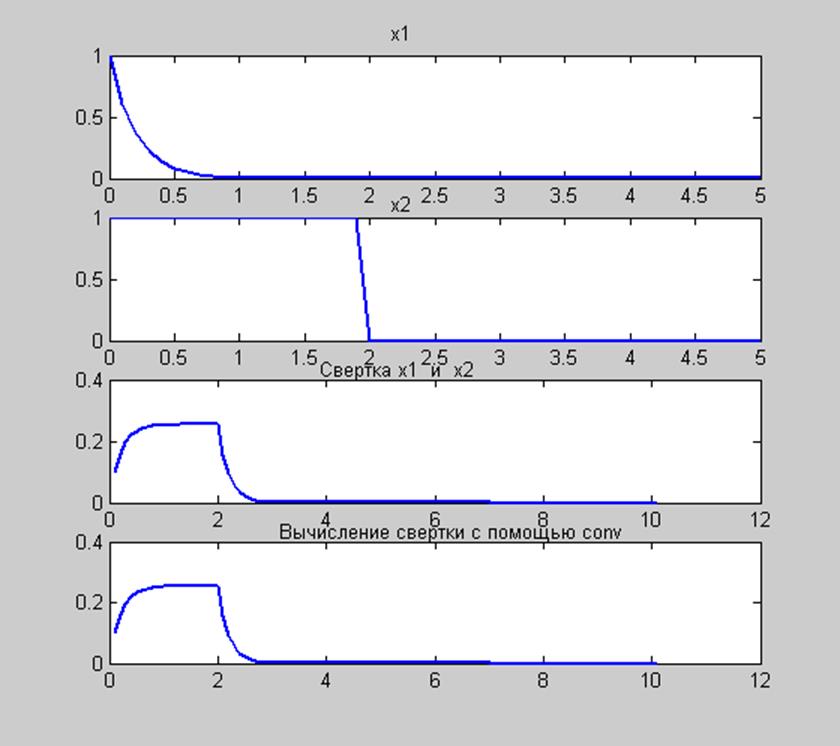
Рис. 1. Графики сигналов и их
свёртки (по выражению (2) и с помощью функции ![]() ).
).
На рис. 1 видим, что графики
свёртки, построенные по выражению (2) и с помощью функции ![]() , совпадают.
, совпадают.
Геометрический смысл операции непрерывной свертки заключается в зеркальном отражении одной из участвующих в операции функций, сдвиге её на значение t, перемножении, интегрировании результата по выражению (1) и повторении операций для другого значения t.
Выполним данные действия для проверки полученных выше результатов.
График зеркально отражённой
функции ![]() представлен на рис.2.
представлен на рис.2.
![]()
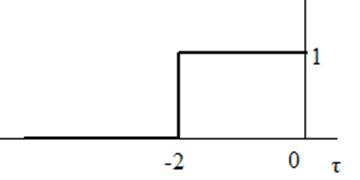
Рис. 2. График зеркально
отражённой функции ![]() .
.
Далее сдвигаем функцию ![]() на t вдоль оси
на t вдоль оси ![]() , перемножаем её с
функцией
, перемножаем её с
функцией ![]() и интегрируем результат на следующих
промежутках:
и интегрируем результат на следующих
промежутках:
1) t<0, x1(τ) и x2(t-τ) не перекрываются, значит y(t)=0
2)
![]() , x1(τ) и x2(t-τ) перекрываются на промежутке
, x1(τ) и x2(t-τ) перекрываются на промежутке ![]()
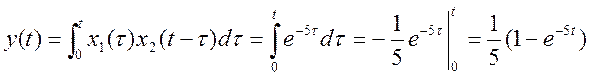
3)
![]() x1(τ) и x2(t-τ) перекрываются на промежутке
x1(τ) и x2(t-τ) перекрываются на промежутке ![]()
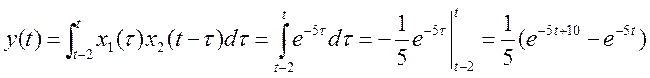
4)
![]() , x1(τ) и x2(t-τ) перекрываются на промежутке
, x1(τ) и x2(t-τ) перекрываются на промежутке ![]()
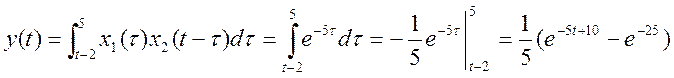
5) ![]() , x1(τ) и x2(t-τ) не перекрываются, значит y(t)=0
, x1(τ) и x2(t-τ) не перекрываются, значит y(t)=0
Таким образом, свёртка сигналов ![]() и
и ![]() имеет
вид (3).
имеет
вид (3).
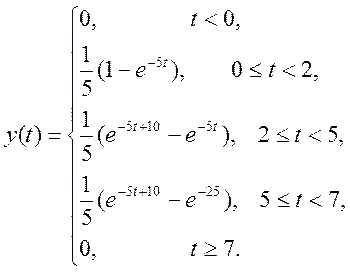 (3)
(3)
График свёртки y(t) представлен на рис. 3.
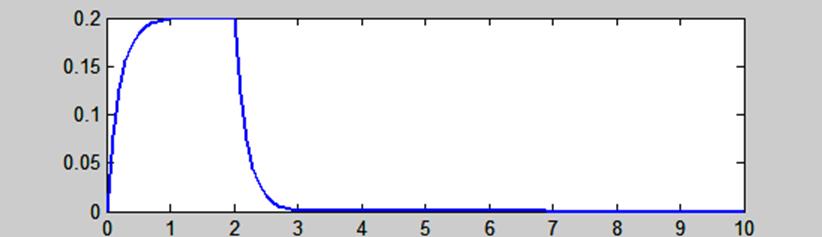
Рис. 3. График свёртки сигналов ![]() и
и ![]() по
выражению (3).
по
выражению (3).
Видим, что графики свёртки, представленные на рис.1 и рис.3 совпадают.
2. Вычисление непрерывной свертки по индивидуальному заданию.
Даны сигналы:
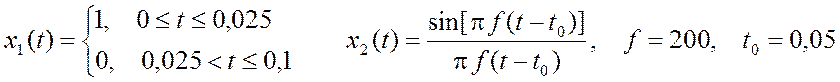
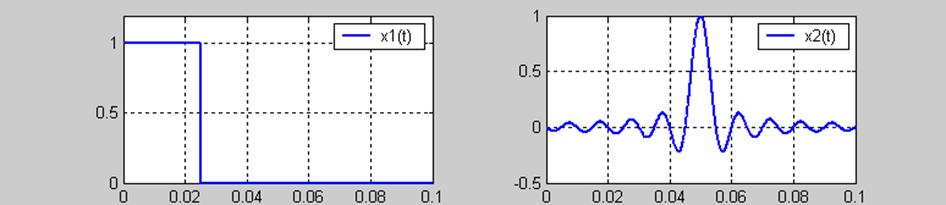
Рис. 4. Сигналы по индивидуальному заданию.
С помощью
следующего script-файла вычислим непрерывную свёртку
сигналов индивидуального задания по выражению (2) и с помощью функции ![]() Matlab, а
также построим графики сигналов и их свёртки.
Matlab, а
также построим графики сигналов и их свёртки.
T=0.00001;
t=0:0.0001:0.1;
x1=rectpuls(t-0.01,0.025); % сигнал x1
t1=0:0.0001:0.1;
x2=sinc(200*(t1-0.05));% сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(t,x1), title('x1')
subplot(412), plot(t,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y),title('Свертка x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
title('Вычисление с помощью conv')
Полученные результаты представлены на рис.5.
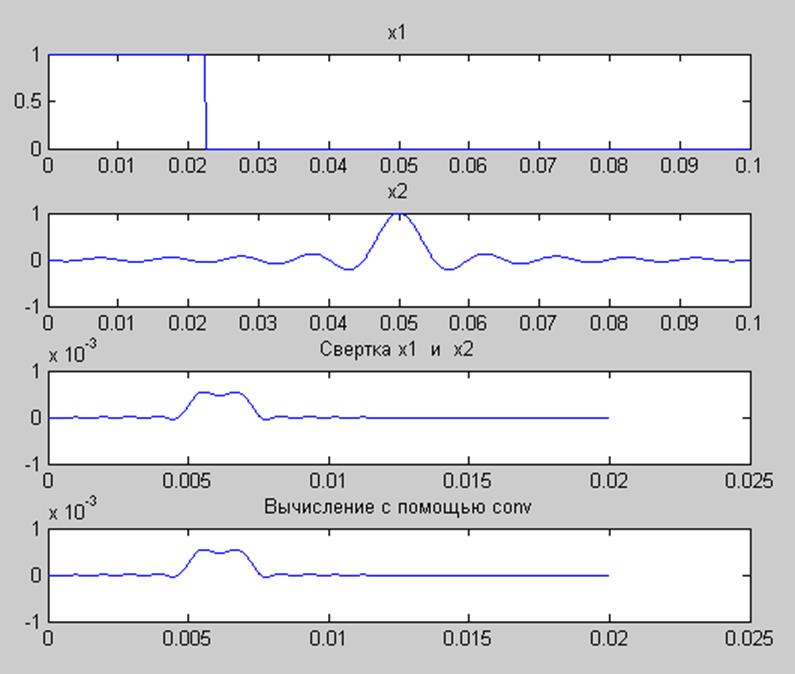
Рис.5. Графики сигналов и их свёртки (по выражению (1)
и с
помощью функции ![]() ).
).
Вычислим свёртку на основе её геометрического смысла для проверки полученного результата.
Разобьём интервал интегрирования на следующие интервалы:
1)t<0, x1(τ) и x2(t-τ) не перекрываются, значит y(t)=0
2) ![]() , x1(τ) и x2(t-τ) перекрываются на промежутке
, x1(τ) и x2(t-τ) перекрываются на промежутке ![]()
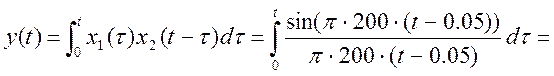
????????????????????????????????
3) ![]() x1(τ) и x2(t-τ) перекрываются на промежутке
x1(τ) и x2(t-τ) перекрываются на промежутке ![]()
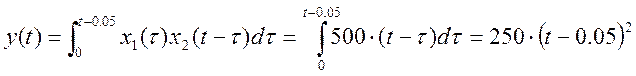
4) ![]() , x1(τ) и x2(t-τ) перекрываются на промежутке
, x1(τ) и x2(t-τ) перекрываются на промежутке ![]()
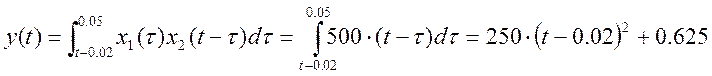
5) ![]() , x1(τ) и x2(t-τ) не перекрываются, значит y(t)=0
, x1(τ) и x2(t-τ) не перекрываются, значит y(t)=0
Таким образом, свёртка сигналов ![]() и
и ![]() имеет
вид (4).
имеет
вид (4).
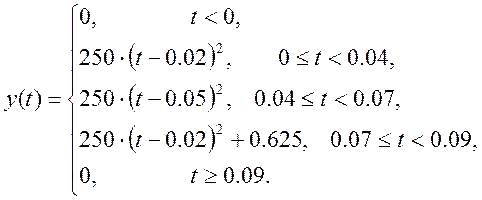 (4)
(4)
График свёртки y(t) представлен на рис.6.
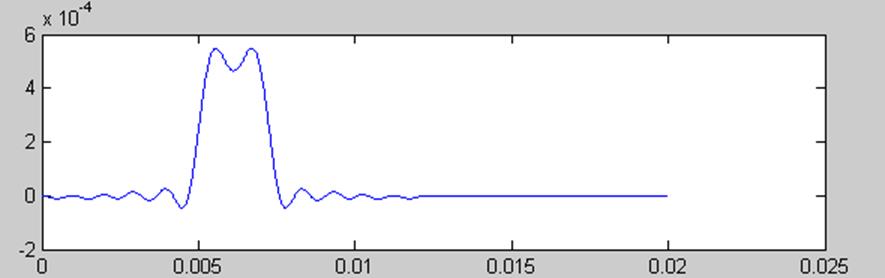
Рис.
6. График свёртки сигналов ![]() и
и ![]() по выражению (4).
по выражению (4).
Видим, что графики свёртки, представленные на рис.5 и рис.6 совпадают.
3. Вычисление дискретной свёртки единичного импульса и последовательности прямоугольных импульсов. +
Функция sqgen() генерирует прямоугольную последовательность импульсов длиной L отсчетов и периодом T отсчетов.
function G=sqgen(L,T)
n=0:1:L;
G = square(T*n/16);
stem(n,G)
C помощью следующего script-файла вычислим свертку единичного импульса delta1=[1] и последовательности sqgen(50, 10), сгенерированной с помощью функции sqgen().
delta1 = [1];
s = sqgen(50,10);
c = conv(delta1,s);
subplot(311), stem(delta1);
title ('delta1 = [1]')
subplot(312), stem(s);
title ('Прямоугольная волна')
subplot(313), stem(c);
title ('Свертка delta1 = [1] и прямоугольной волны')
Полученные результаты представлены на рис.7.
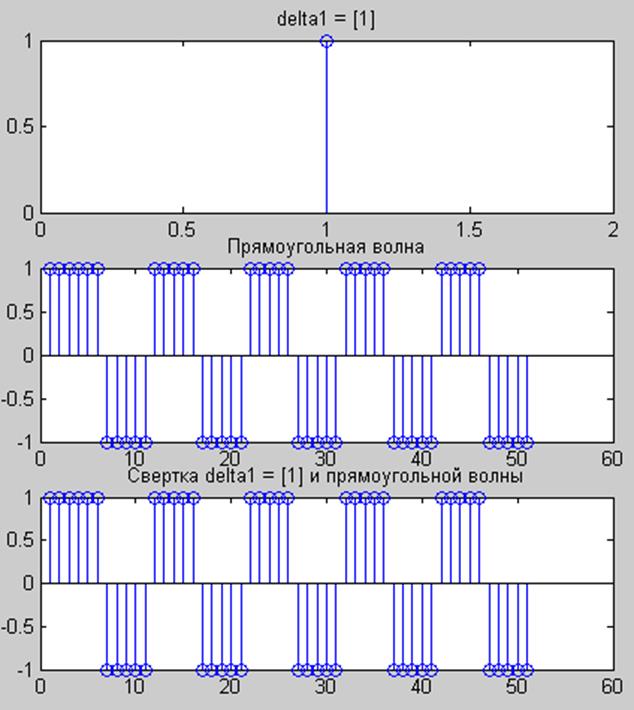
Рис. 7. Графики сигнала sqgen(50,10), единичного
импульса delta1=[1] и их свёртки.
На рис. 7 видим, что график последовательности прямоугольных импульсов совпадает с графиком его свёртки с единичным импульсом.
Свёртка любого сигнала ![]() с единичным импульсом даёт исходный
сигнал, т.е.
с единичным импульсом даёт исходный
сигнал, т.е. 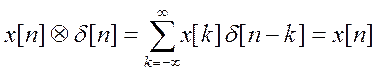 .
.
Это объясняется тем, что для
любого n произведение ![]() только при k=n и размер свёртки N = N1 + N2 – 1 = 50 + 1 – 1 = 50.
только при k=n и размер свёртки N = N1 + N2 – 1 = 50 + 1 – 1 = 50.
C помощью следующего script-файла вычислим свертку единичного импульса
delta2=[1 zeros(1,9)] и последовательности sqgen(50, 10), сгенерированной с помощью функции sqgen().
delta2=[1 zeros(1,9)]
[t,y]=sqgen(50,10);
c = conv(delta2, y);
subplot(3,1,1);
stem(t,y);
title('График последовательности импульсов sqgen(50,10)')
n = 0:9;
subplot(3,1,2);
stem(n,delta2);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('График единичного импульса delta2=[1 zeros(1,9)]')
subplot(3,1,3);
t = 0: length(y)+length(delta2)-2;
stem(t,c);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('График свёртки sqgen(50,10) и delta2=[1 zeros(1,9)]')
Полученные результаты представлены на рис.8.
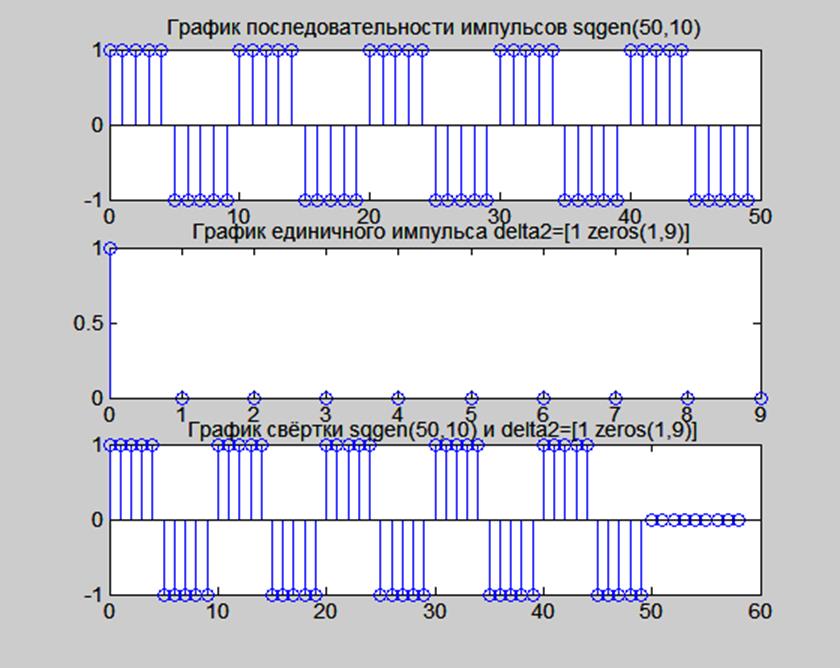
Рис.8. Графики сигналов sqgen(50,10) и
delta2=[1 zeros(1,9)] и их свёртки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.