На рис. 8. видим, что первые 50 отсчётов свёртки повторяют сигнал sqgen(50, 10), что совпадает с результатом, представленным на рис.7, а остальные 9 отсчётов нулевые.
Таким образом, добавление 9 нулей к единичному импульсу delta1=[1] повлекло за собой только увеличение размера свёртки (т.к. N = N1 + N2 – 1 = 50 + 10 – 1 = 59) и заполнение дополнительных отсчётов нулями, но не изменение формы сигнала.
4. Вычисление свёртки последовательности прямоугольных импульсов и плоских импульсов различной длины.
C помощью следующего script-файла вычислим свертку плоского импульса
длиной N = 3 и N = 8 отсчётов и последовательности sqgen(50, 10).
N = 8;
h1=[ones(1,N)]
[t,y]=sqgen(50,10);
c = conv(h1, y);
subplot(3,1,1);
stem(t,y);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('График последовательности импульсов sqgen(50,10)')
n = 0:N-1;
subplot(3,1,2);
stem(n,h1);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title(['График плоского импульса с числом отсчётов N=',num2str(N)])
subplot(3,1,3);
n = 0:length(h1)+length(y)-2;
stem(n,c);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('График свёртки sqgen(50,10) и плоского импульса')
Полученные результаты представлены на рис.9,10.
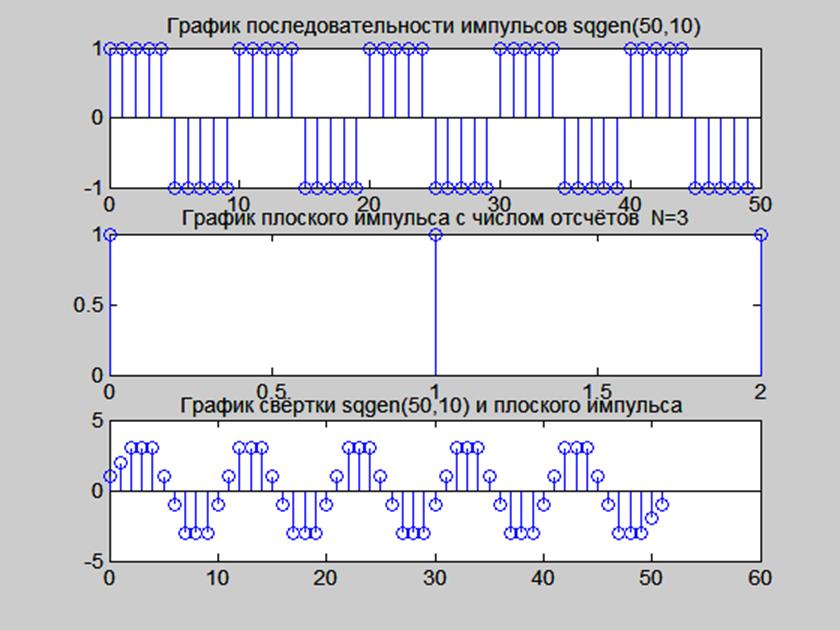
Рис.9. График сигнала sqgen(50,10), плоского импульса длиной 3 отсчёта и их свёртки.
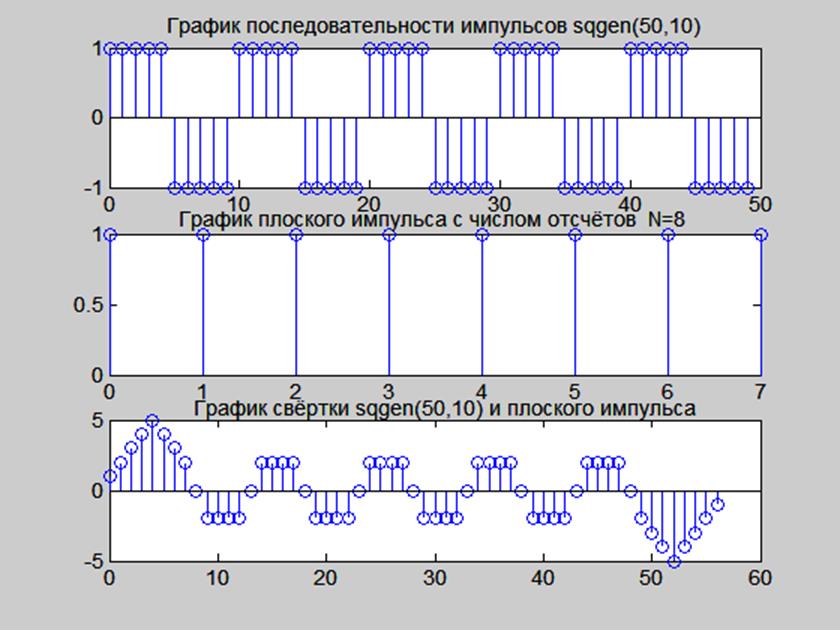
Рис.10. График сигнала sqgen(50,10), плоского импульса
длиной 8 отсчётов и их свёртки.
При изменении длины плоского импульса форма свёртки изменяется, в отличие от дополнения последовательности нулями.
При увеличении длины импульса h1 форма свёртки приближается к последовательности треугольных импульсов амплитудой 5 (5 положительных и 5 отрицательных).
5. Вычисление свёртки двух сигналов и восстановление из неё сигнала с помощью операции обратной свёртки.
Даны сигналы 
и 
вида
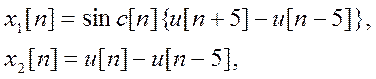(5)
(5)
где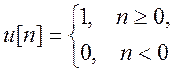 
-
дискретная единичная ступенчатая функция.
С помощью следующего script-файла вычислим свёртку сигналов и и
восстановим из неё сигнал с помощью функции
deconv().
T=1; % шаг дискретизации
t = -5:T:5;
t1 = 0:4;
x1=sinc(t/pi); % сигнал x1
x2 = [ones(1,5)]; % сигнал x2
n1=length(x1);
n2=length(x2);
subplot(411), stem(t,x1)
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('Сигнал x1')
subplot(412), stem(t1,x2)
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('Сигнал x2')
k1=0:n1+n2-2;
% вычисление свертки с помощью функции conv()
c=conv(x1,x2);
subplot(413), stem(k1*T,T*c)
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('Свёртка сигналов x1 и x2')
Q = deconv(c,x2);
subplot(4,1,4);
stem(t,Q);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('Cигнал x1, восстановленный из свёртки')
Полученные результаты представлены на рис. 11.
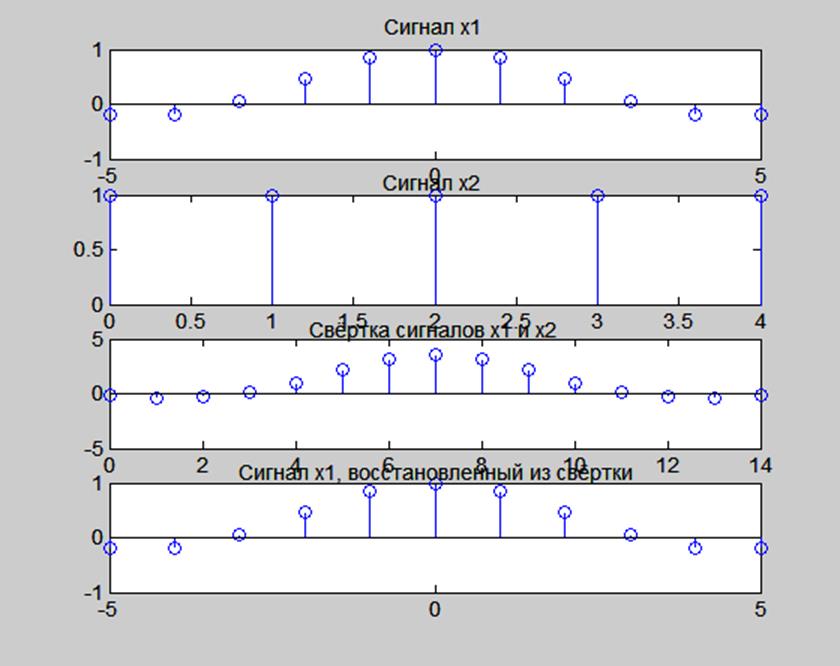
Рис.
11. Графики сигналов и ,
их свёртки
и
восстановленного из неё .
На рис. 11 видим, что график
сигнала , восстановленный из свёртки,
совпадает с исходным сигналом .
Функция deconv() позволяет выполнять обратную операцию свёртки и тем самым восстанавливать из свёртки один из сигналов, зная свёртку и другой сигнал.
На практике с помощью обратной свёртки можно, например, найти импульсную характеристику ЛДС, зная входной и выходной сигналы, т.к. выходной сигнал ЛДС определяется как дискретная свертка входного сигнала x[n] и импульсной характеристики h[n] системы.
6. Вычисление свёртки сигналов в частотной и временной области.
Вычисление свёртки в частотной области проводится на основе свойства свёртки ДПФ:
Если 
,
то 
Так как ДПФ является периодическим, дискретная свёртка, вычисленная с его помощью, также является периодической (круговая свёртка). Из-за периодичности ДПФ возникает эффект «перекрытия». Чтобы этого избежать необходимо увеличить период ДПФ за счёт увеличения его размера L.
Для этого исходные последовательности дополняют нулями так, чтобы их длина была больше или равна длине линейной свёртки N = N1 + N2 – 1.
При этом полученная свёртка будет иметь (L – N) нулевых отсчётов.
С помощью следующего script-файла вычислим свёртку экспоненциально убывающего и прямоугольного сигналов во временной и частотной области, а также найдём время их вычисления.
T=0.1; % шаг дискретизации
i1 = 0:T:9.9;
x1=exp(-2*i1); % сигнал x1
i2 = 0:T:3.9;
x2 = rectpuls(i2-10,20); % сигнал x2
n1=length(x1);
n2=length(x2);
subplot(411), stem(i1,x1)
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('Сигнал x1')
subplot(412), stem(i2,x2)
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('Сигнал x2')
k1=1:n1+n2-1;
% вычисление свертки с помощью функции conv()
t1 = cputime;
c=conv(x1,x2);
t2 = cputime-t1
subplot(413), stem(k1*T,T*c)
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('Свёртка сигналов x1 и x2 во временной области')
x3 = [x1 zeros(1,156)];
x4 = [x2 zeros(1,216)];
t3 = cputime;
X = fft(x3).*fft(x4);
x = ifft(X);
t4 = cputime-t3
subplot(4,1,4);
k = 1:256;
length(x4)
stem(T*k,T*x);
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('Свёртка сигналов x1 и x2 в частотной области')
Полученные результаты представлены на рис. 12.
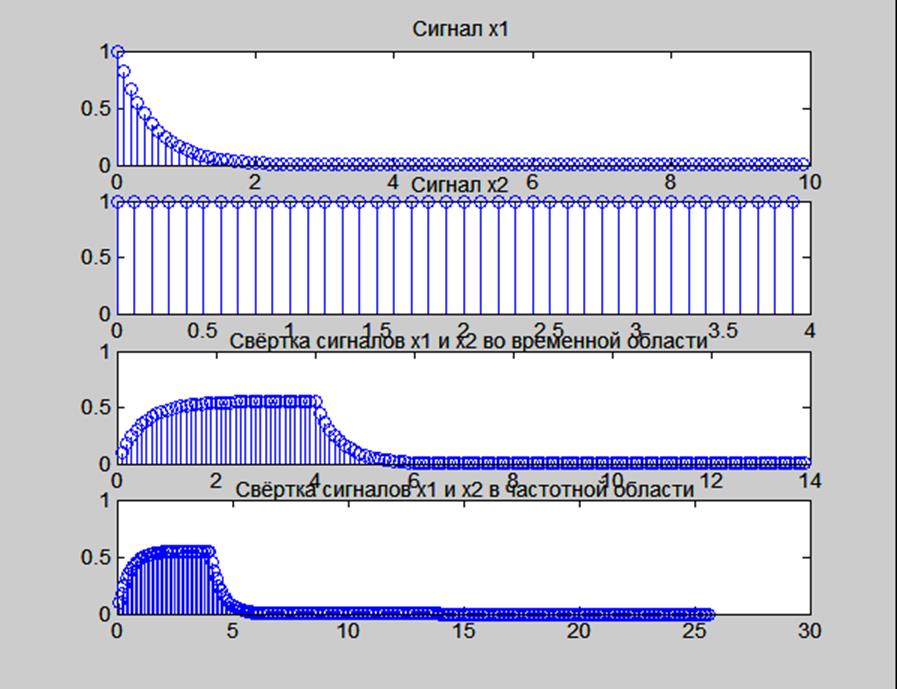
Рис.12. График сигналов и их свёртки, вычисленной
во временной и частотной области.
Для сравнения свёрток сигналов, вычисленных во временной и частотной области, увеличим фрагмент рис.12.
Результат представлен на рис.13.
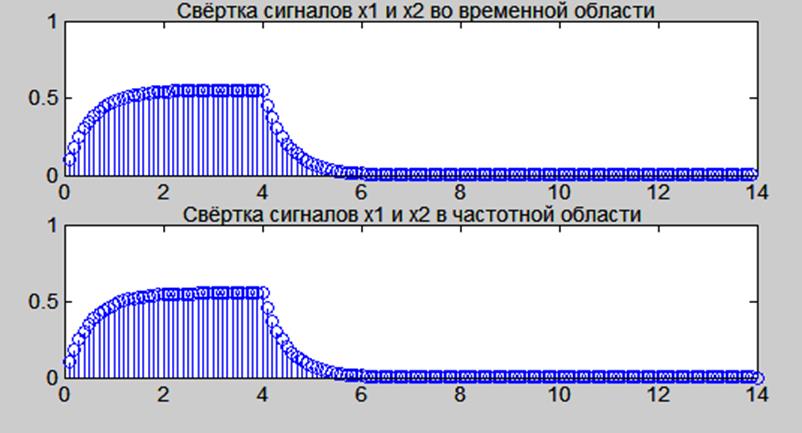
Рис.13. Графики свёртки сигналов x1 и x2, вычисленной во временной и частотной области.
На рис.13 видим, что свёртки сигналов, вычисленные во временной и частотной области совпадают, значит, свойство свёртки выполняется.
На рис.12 видим, что круговая свёртка имеет на L – N = 256 – 139 = 115 нулевых отсчётов больше, чем линейная свёртка, что является результатом дополнения исходных последовательностей нулями.
Время вычисления линейной и круговой свёрток равно 0.0310 и 0.0150 сек. соответственно, т.е. круговая свёртка вычисляется в 2 раза быстрее линейной.
Это объясняется тем, что линейная
свертка сигналов длительностью М и N отсчетов
требует приблизительно N*M
операций, а вычисление круговой свёртки с использованием БПФ требует примерно
операций, где L
– размер БПФ.
В нашем случае N*M = 100*40 = 4000 и 
, т.е. круговая свёртка практически в
2 раза быстрее линейной, что совпадает с опытными данными.
При увеличении исходного размера сигналов выигрыш по времени вычисления будет увеличиваться.
Выводы:
1. Непрерывная свёртка определяется выражением
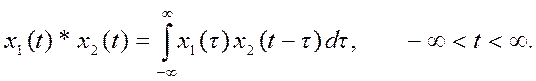
Дискретная свёртка определяется выражением
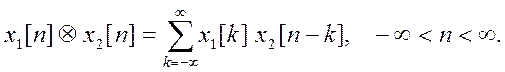
2. Непрерывную свёртку можно вычислить численным методом с помощью выражения
,
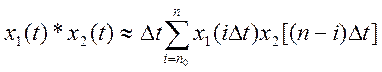где 
- интервал дискретизации.
В п.1 было показано, что результаты вычисления свёртки с помощью данного выражения совпадают с результатами, полученными с помощью функции conv() и на основе геометрического смысла операции свёртки.
3. В п. 3 показали, что свёртка
любого сигнала 
с единичным импульсом даёт
исходный сигнал, т.е. 
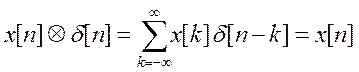и дополнение
импульса нулями приводит только к увеличению размера свёртки за счёт нулевых
отсчётов (рис.7, 8).
4. В п.6. показали, что использование круговой свёртки позволяет существенно увеличить скорость вычисления (в нашем случае в 2 раза), но требует дополнения сигналов нулями для избавления от эффекта «перекрытия».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.