НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
ЛАБОРАТОРНАЯ РАБОТА № 5
НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ СВЕРТКИ
Вариант 10
Выполнили:
Группа: АИ-72
Студент: Спитченко В.М.
Преподаватель: Щетинин Ю.И.
Новосибирск 2004
Цель работы:Изучение понятия и свойств непрерывной и дискретной свертки, приобретение практических навыков вычисления свертки в среде Matlab.
1.
Свертка двух непрерывных по
времени сигналов (непрерывная свертка) определяется выражением
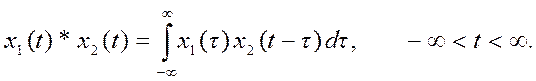
Численное вычисление непрерывной свертки может быть аппроксимировано конечной
суммой вида
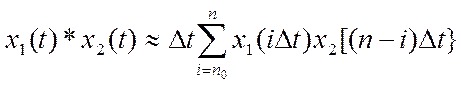 ,
,
где
![]() - интервал (шаг) дискретизации.
- интервал (шаг) дискретизации.
Ознакомиться с процедурой для приближенного вычисления непрерывной свертки
сигнала прямоугольной формы и экспоненциального сигнала. Выполнить процедуру и
объяснить её результаты.
М-файл для численного вычисления непрерывной свертки:
T=0.1; % шаг дискретизации
a=5;
i=0:50;
x1=exp(-a*i*T); % сигнал x1
x2=rectpuls(i-10,20); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(i*T,x1), title('x1')
subplot(412), plot(i*T,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y),title('Свертка x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
title('Вычисление с помощью conv')
Результат выполнения:
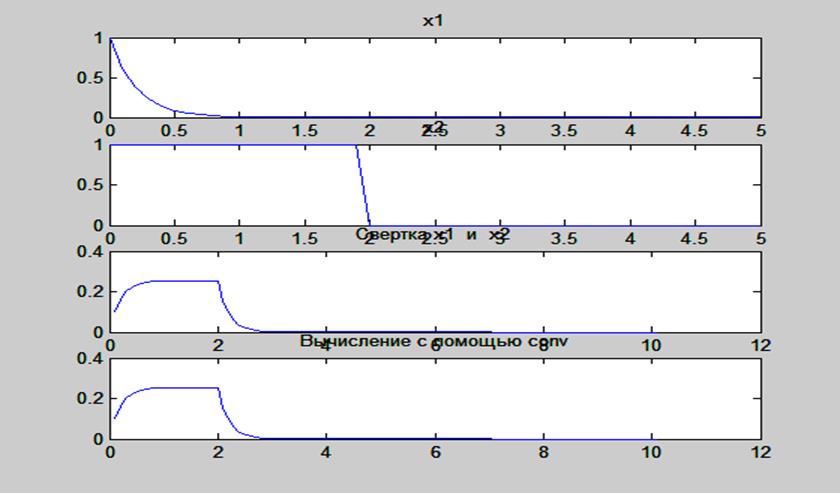
Рис.1. Графики сигналов и их свертки, вычисленной численным методом и при помощи
функции conv().
По полученным графикам видно, что свертка сигналов, выполненная численным методом совпадает со сверткой, вычисленной при помощи встроенной функции conv().
2. Написать и выполнить процедуру вычисления непрерывной свертки по индивидуальному заданию.
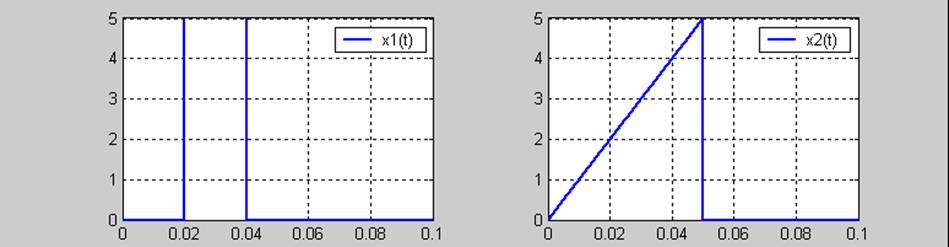
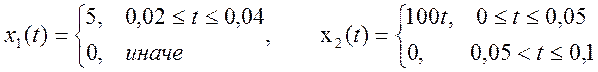
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
М-файл для численного вычисления непрерывной свертки:
T=0.001; % шаг дискретизации
i=0:100;
t=0:0.0001:0.1;
x1=rectpuls(i,50); --- не пашет!!!
%x2 = sinc(pi.*200.*(t-0.05));
x2 =100*t;
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(i*T,x1), title('x1')
subplot(412), plot(t,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y),title('Свертка x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
title('Вычисление с помощью conv')
Результат выполнения:
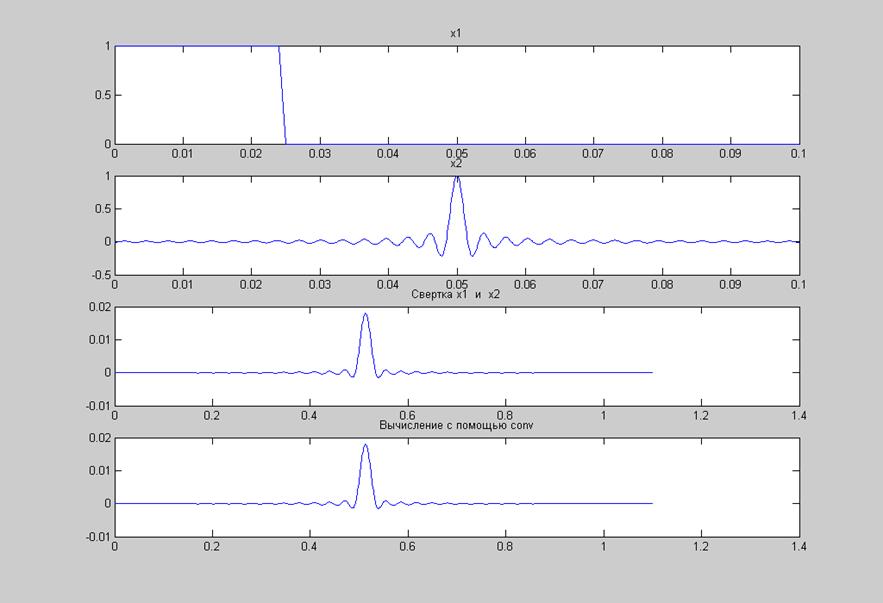
Рис.2. Графики сигналов и их свертки, вычисленной численным методом и при помощи
функции conv().
По полученным графикам видно, что свертка сигналов, выполненная при помощи численного вычисления совпадает со сверткой, вычисленной при помощи встроенной функции conv().
3. Написать Matlab – функцию sqgen(L,T) с двумя параметрами L и T, которая генерирует прямоугольную последовательность импульсов длиной L отсчетов и периодом T отсчетов.
Функция sqgen():
function y=sqgen(L,T) %определение функции
t=0:L-1; %определение временного интервала
y=square(2*pi*t/T);%генерирование прямоугольной
%последовательности
4. Создать единичный импульс delta1=[1]. Вычислить свертку delta1 sqgen(50, 10). Построить с помощью stem() графики сигналов и результата свертки.
М-файл для вычисления свертки delta1 и sqgen(50, 10):
delta1=[1];%определение единичного импульса
figure;
subplot(311),stem(delta1);
y=sqgen(50,10);% генерирование прямоугольной последовательности
subplot(312),stem(y);
sver=conv(delta1,y);%вычисление свертки сигналов
subplot(313),stem(sver);
Результат выполнения:
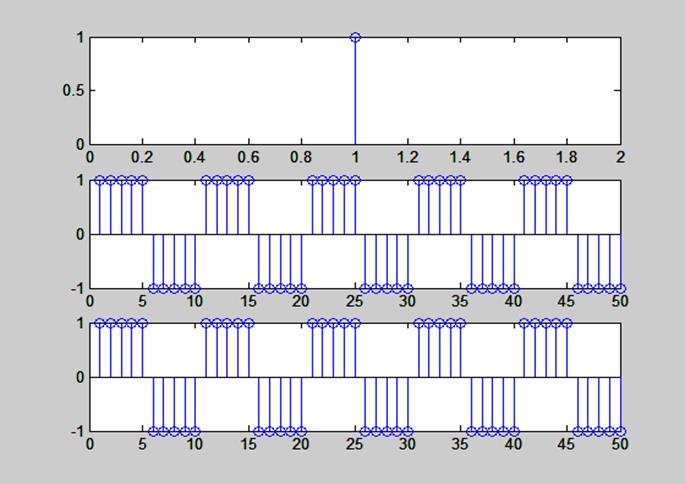
Рис.3. Графики сигналов delta1, sqgen(50, 10) и их свертка
Очевидно, что свертка сигналов в точности повторяет сигнал sqgen(50, 10). При каждом n значение свертки определяется как соответствующее значение сигнала sqgen(50, 10), умноженное на единицу; все остальные слагаемые свертки зануляются.
Размер свертки – 50 отчетов: 50+1-1=50.
Таким образом, единичный импульс, как один из сигналов, входящих в свертку, позволяет получить при вычислении свертки другой сигнал.
5. Создать с помощью команды delta2=[1 zeros(1,9)] другой импульс и вычислить свертку delta2 и sqgen(50, 10). Построить графики.
М-файл для вычисления свертки delta2 и sqgen(50, 10):
delta2=[1 zeros(1,9)]; %генерирование импульса
figure;
subplot(311),stem(delta2);
y=sqgen(50,10); %генерирование прямоугольной последовательности
subplot(312),stem(y);
sver=conv(delta2,y); %вычисление свертки
subplot(313),stem(sver);
Результат выполнения:
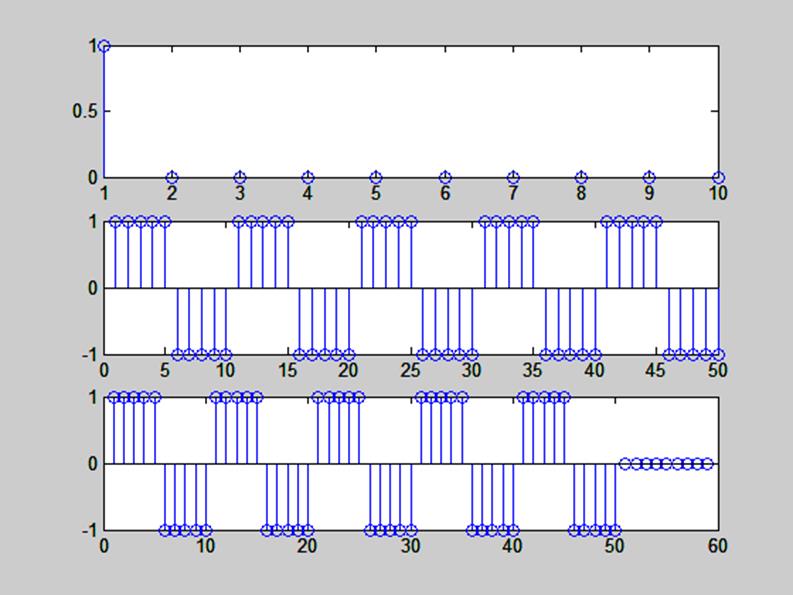
Рис.4. Графики сигналов delta2, sqgen(50, 10) и их свертка
Размер свертки – 59 отчетов, т.е. N1+N2-1, где N1 – кол-во отчетов первого сигнала, N2 – кол-во отчетов второго сигнала. Первые 50 отчетов представляют собой сигнал sqgen(50, 10); 9 последних отчетов заполнены нулями, поскольку в первом сигнале со второго по десятый отсчеты - нули.
6. Создать плоский импульс с помощью команды h1=[ones(1,2)]. Вычислить свертку h1 и sqgen(50, 10). Построить графики сигналов и свертки. Увеличить длину импульса до 8, снова вычислить свертку и постройте её график. Объяснить различия.
М-файл для вычисления свертки сигналовh1=ones(1,2) и sqgen(50, 10):
h1=[ones(1,2)] %определение плоского импульса
figure;
subplot(311),stem(h1);
y=sqgen(50,10); %генерирование прямоугольной последовательности
subplot(312),stem(y);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.