Изучение понятия и свойств непрерывной и дискретной свертки. Вариант 10, страница 2

sver=conv(h1,y); %вычисление сверки сигналов

subplot(313),stem(sver);

Результат выполнения:

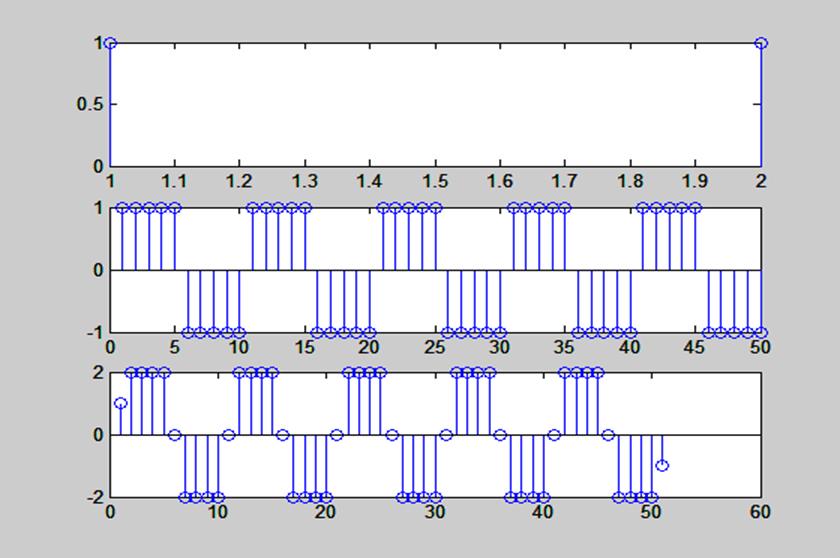
Рис.5. Графики сигналов h1=ones(1,2),  sqgen(50, 10) и их свертка

Длина свертки – 51 отсчет.

Вид свертки данных сигналов изменился по сравнению со сверткой, выполненной в предыдущем пункте из-за того, что сигнал h1=ones(1,2) представляет собой 2 единичных импульса.

Увеличиваем длительность плоского импульса до 8.

М-файл для вычисления свертки сигналовh1=ones(1,8) и  sqgen(50, 10):

h1=[ones(1,8)] %определение плоского импульса

figure;

subplot(311),stem(h1);

y=sqgen(50,10); %генерирование прямоугольной последовательности

subplot(312),stem(y);

sver=conv(h1,y); %вычисление свертки сигналов

subplot(313),stem(sver);

Результат выполнения:

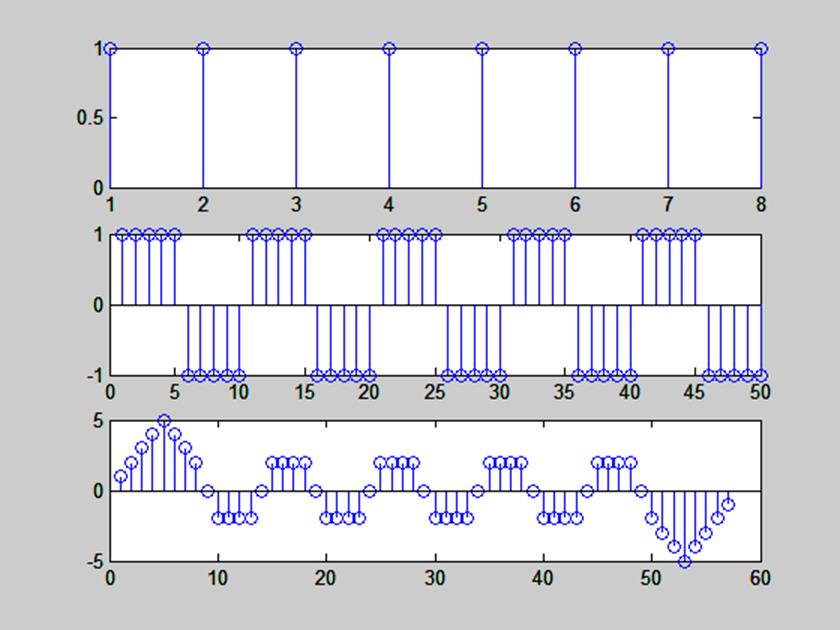
Рис.6. Графики сигналов h1=ones(1,8),  sqgen(50, 10) и их свертка

Длина свертки – 57 отсчетов.

Значения первых и последних 8 отсчетов свертки равномерно увеличиваются и уменьшаются на 1 в зависимости от того положительные или отрицательные значения имеет сигнал sqgen(50, 10) в соответствующих отсчетах. На остальных отсчетах свертка представляет собой прямоугольную последовательность амплитуды 2 с нулевыми значениями в 9, 14, 19, 24, 29 и т.д. отсчетах.

При увеличении длительности сигнала h1 вид свертки будет все больше приближаться к треугольной последовательности амплитуды 5. Т.е. значение каждого последующего отсчета будет на 1 отличаться от предыдущего в зависимости от знака сигнала sqgen(50, 10) в соответствующем отсчете.

7.  Вычислить свертку сигналов

                                   

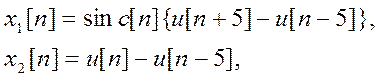
где 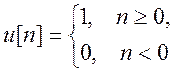     - дискретная единичная ступенчатая функция.

Построить графики сигналов и  их свертки.
      С помощью функции deconv()  восстановить сигнал    из свертки, построить график результата.

Функция для определения дискретной единичной ступенчатой функции:

function u=fun(t)

for i=1:length(t)

    if t(i)>=0

        u(i)=1;

    end

    if t(i)<0

        u(i)=0;

    end

end

М-файл для генерирования сигналов, вычисления их свертки и восстановления сигнала из свертки:

T=5;

t=-T:T; %определение временного интервала

tt=0:T;

t1=tt-5;

t2=tt+5;

u=fun(tt); %определение функции u(t)

u1=fun(t1); %определение функции u(t-5)

u2=fun(t2); %определение функции u(t+5)

figure(1);

subplot(311), stem(tt,u); title('u(t)');

subplot(312), stem(tt,u1); title('u(t-5)');

subplot(313), stem(tt,u2); title('u(t+5)');

t1=0:T;

x1=sinc(t/pi); %определение сигналов

x2=u-u1;

x=conv(x1,x2); %вычисление свертки сигналов

figure(2);

subplot(411), stem(t,x1),title('x1');

subplot(412), stem(t1,x2),title('x2');

subplot(413), stem(x), title('conv')

x3=deconv(x,x2); %выделение сигнала х1 из свертки

subplot(414), stem(t,x3), title('deconv')

Поскольку в первом отсчете сигнала х2, являющегося одним из параметров функции deconv(x,x2), не может быть ноль, ограничимся лишь соответствующими положительным отсчетам значениями сигнала х2.

Графики сигналов х1, х2, их свертка и выделение сигнала х1 из свертки:

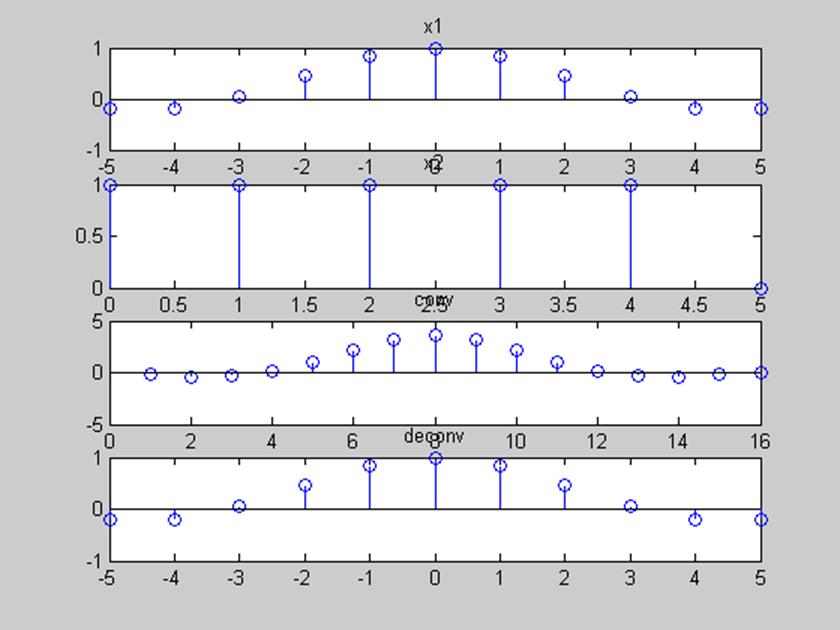
Рис.9. Графики сигналов х1, х2, их свертка и выделение сигнала х1 из свертки

Из построенных графиков видно, что результат функции deconv() в точности совпадает с исходным сигналом х1.

8.  Сгенерировать экспоненциальный дискретный сигнал длительностью 100 отсчетов и прямоугольный сигнал из 40 отсчетов. Выполнить дискретную свертку этих сигналов и представить её график. Далее выполнить свертку этих сигналов с помощью БПФ.

М-файл для генерирования двух сигналов и выполнения их свертки:

%генерирование экспоненциального сигнала

n1=0:0.01:0.99;

y1=exp(n1);

%генерирование экспоненциального сигнала

n2=0:0.01:0.39;

for i=1:40

    y2(i)=1;

end

%вычисление свертки сигналов

y=conv(y1,y2);

figure;

subplot(211), stem(n1,y1)

hold on

stem(n2,y2,'g');

subplot(212), stem(y);

Результат выполнения:

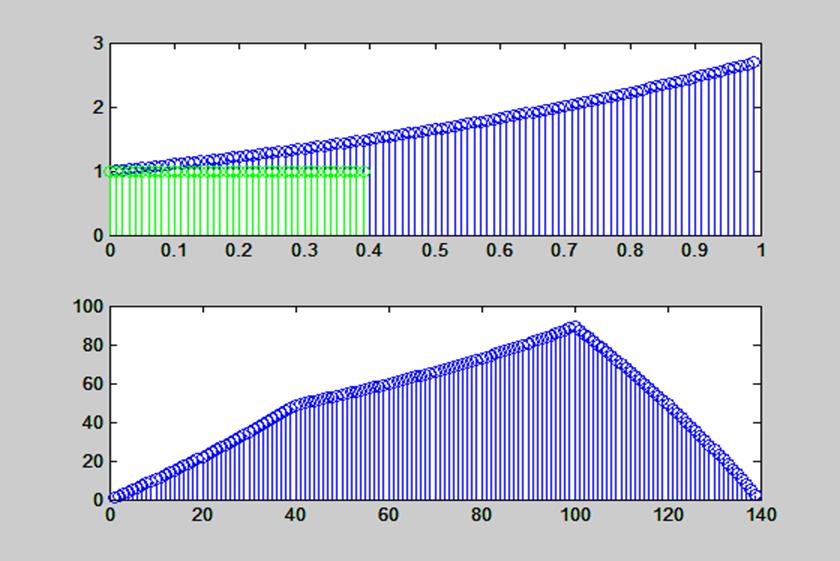
Рис. 18. Графики экспоненциального и прямоугольного сигналов и их свертка, 

              выполненная при помощи функции conv()

Размер свертки – 139 отсчетов: 100+40-1.

Значения свертки, соответствующие первым 100 отсчетам  равномерно увеличиваются, однако, начиная с сорокового отсчета характер свертки меняется, поскольку зануляются первые слагаемые при вычислении свертки. Начиная с сотого отсчета свертка начинает убывать, т.к. зануляются слагаемые свертки, соответствующие большим значениям экспоненциального сигнала.

М-файл для  выполнения круговой свертки сигналов:

%генерирование экспоненциального сигнала

n=0:0.01:0.99;

y1=exp(n);

%генерирование экспоненциального сигнала

n2=0:0.01:0.39;

for i=1:40

    y2(i)=1;

end

%дополнение последовательностей нулями

y1z=[y1 zeros(1,156)];

y2z=[y2 zeros(1,216)];

%вычисление ДПФ последовательностей

y1f=fft(y1z);

y2f=fft(y2z);

yf=y1f.*y2f; %произведение ДПФ последовательностей

x=ifft(yf); %ОДПФ произведения

figure;

n1=0:0.01:2.55;

n2=0:0.01:2.55;

subplot(211),

stem(n1,y1z)

hold on

stem(n2,y2z,'g');

subplot(212), stem(abs(x));

title('Круговая свертка')

Результат выполнения:

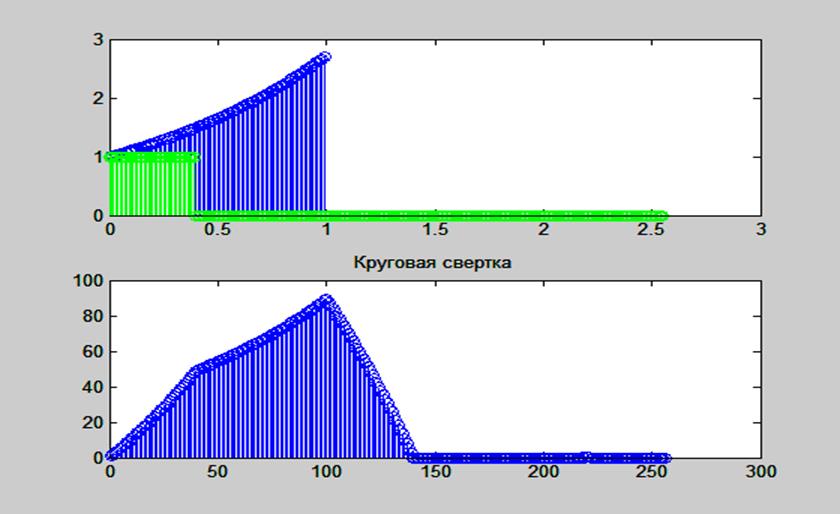
Рис. 19. Графики экспоненциального и прямоугольного сигналов, дополненных нулями и их  

              круговая свертка. 

Размер круговой свертки равен размеру каждого из сигналов – 256 отсчетов. Первые 139 отсчетов в точности повторяют свертку, выполненную с помощью функции conv(). Следующие 117 отсчетов заполнены нулями. Круговая свертка имеет периодический характер, из-за этого возникает эффект «перекрытия». Для исключения перекрытия следует использовать ДПФ с N большим N1+N2-1. Для этого сигналы следует дополнить нулями.

Этот метод вычисления свертки конечных последовательностей называется быстрой сверткой. Быстрая свертка эффективнее прямой уже при (N1+N2-1) больше 30 и выше. Это обеспечивается за счет быстрых алгоритмов вычисления ДПФ.