Информатика и выч. техника \ Теория и обработка сигналов

Изучение понятия и свойств непрерывной и дискретной свертки. Вариант 3

Страницы работы

17 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Кафедра Систем Сбора и Обработки Данных

Дисциплина «Теория и обработка сигналов», 5 - й семестр

ЛАБОРАТОРНАЯ РАБОТА № 5

НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ СВЕРТКИ

Вариант № 3

Студент гр. АО-81

Васильева И.В.

Преподаватель

Доц. Щетинин Ю.И.

Новосибирск

2010

Цель работы:Изучение понятия и свойств непрерывной и дискретной свертки, приобретение практических навыков вычисления свертки в среде Matlab.

1. Выполнение и объяснения процедуры вычисления приближенного непрерывной свертки сигнала прямоугольной формы и экспоненциального сигнала.

% Численное вычисление непрерывной свертки

T=0.1; % шаг дискретизации

a=5;

i=0:50;

x1=exp(-a*i*T); % сигнал x1

x2=rectpuls(i-10,20); % сигнал x2

n1=length(x1);

n2=length(x2);

figure(2),subplot(411), plot(i*T,x1), title('x1')

subplot(412), plot(i*T,x2), title('x2')

k1=1:n1+n2-1;

% вычисление свертки

for n=1:n1+n2-1,

y(n)=0;

for k=max(1,n+1-n1):min(n,n2),

y(n)=y(n)+sum(x1(n+1-k)*x2(k));

end

y(n)=y(n)*T;

end

% график свертки сигналов

subplot(413), plot(k1*T,y),title('Свертка x1 и x2')

% вычисление свертки с помощью функции conv()

subplot(414), plot(k1*T,T*conv(x1,x2))

title('Вычисление свертки с помощью conv')

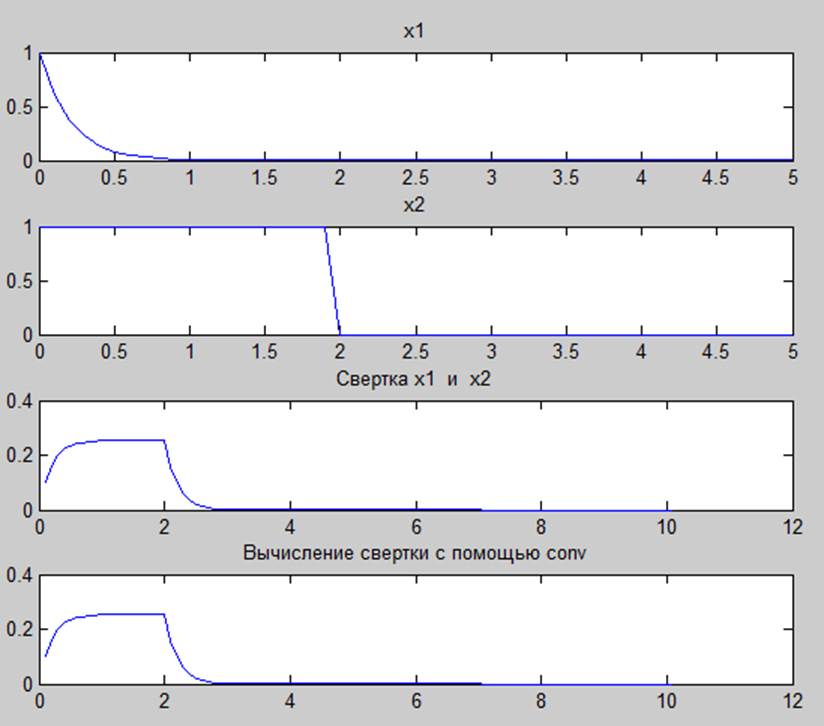
Рис.1. Графическое изображение сигналов : , и их свертка

Графики свёртки, построенные по выражению

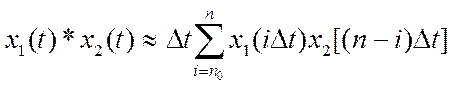
и с помощью функции , совпадают, следовательно, каждый из этих способов можно применять для вычисления непрерывной свертки.

Геометрический смысл операции непрерывной свертки в данном примере состоит в отображении зеркально экспоненциальной функции и смещение ее, дальше суммируем сигналы и получаем свертку. Сначала экспонента возрастает из-за зеркального отображения, остается постоянной из-за суммирование ее с единичной функцией и экспоненциально убывает из-за сложения ее со второй функции.

2. Выполнение процедуры вычисления непрерывной свертки по индивидуальному заданию.

Вариант №3

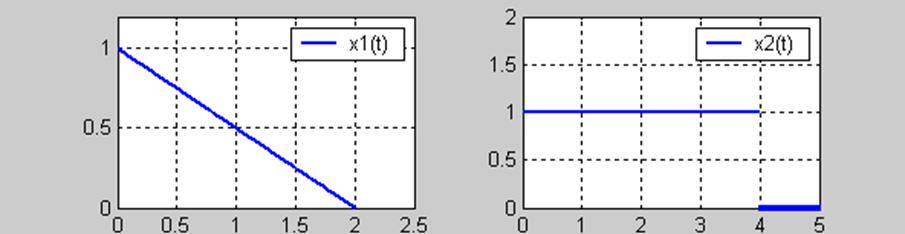
t=0:0.01:2;

T=0.01; % шаг дискретизации

i=0:5/T;

x1=1-(t)*0.5; % сигнал x1

x2=rectpuls(i-2/T,4/T); % сигнал x2

n1=length(x1);

n2=length(x2);

k1=1:n1+n2-1;

% вычисление свертки

for n=1:n1+n2-1,

y(n)=0;

for k=max(1,n+1-n1):min(n,n2),

y(n)=y(n)+sum(x1(n+1-k)*x2(k));

end

y(n)=y(n)*T;

end

figure(3),

subplot(411), plot((0:n1-1)*T,x1), title('x1'), grid

subplot(412), plot(i*T,x2), title('x2'), grid

% график свертки сигналов

subplot(413), plot((0:length(y)-1)*T,y), grid

axis([0 (length(y)-1)*T 0 1.2*max(y)]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Свертка x1 и x2')

% вычисление свертки с помощью функции conv()

subplot(414), plot((0:length(conv(x1,x2))-1)*T,T*conv(x1,x2)), grid

axis([0 (length(y)-1)*T 0 1.2*max(y)]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);

title('Вычисление свертки с помощью conv')

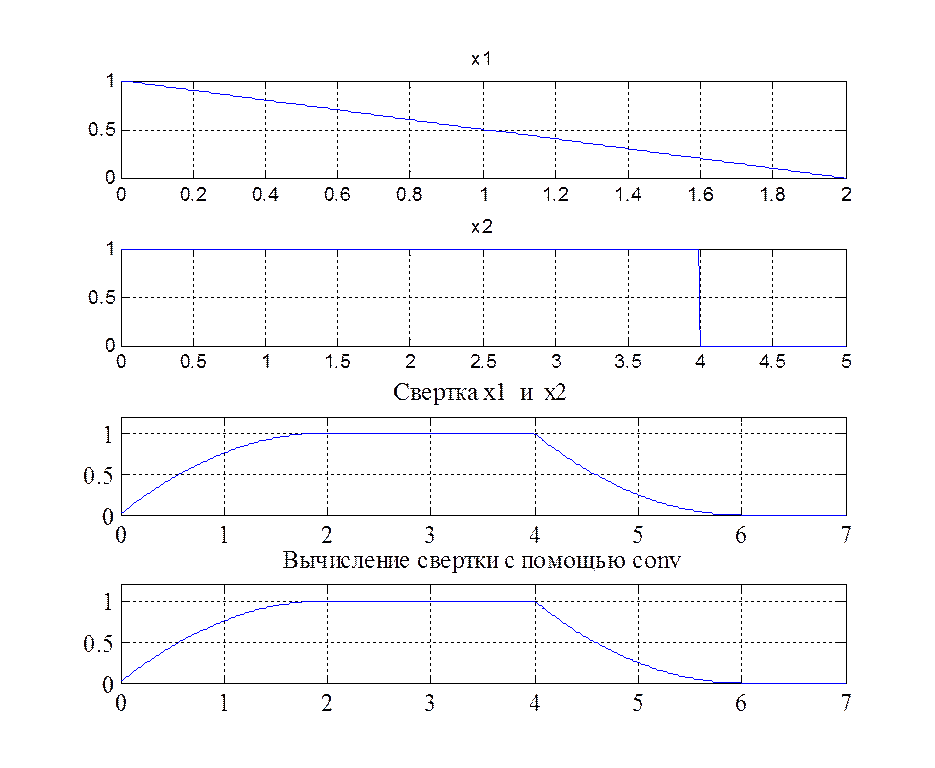
Рис.3. График сигналов и , их свертка.

Вычисление линейной свертки с помощью конечных сумм и с помощью функции conv приводят к одинаковым результатам.

Выполняем свертку треугольного импульса и единичного: зеркально отображаем функцию x1 и смещаем, дальше накладывается 2 исходных сигнала, и в результате суммирование сначала функция возрастает, потом из-за единичного импульса остается неизменной на единице, дальше она экспоненциально убывает.

3. Написание Matlab – функции sqgen(L,T), которая генерирует прямоугольную последовательность импульсов.

function y=sqgen(L,T) % Определение функции

t=0:L-1; % Определение временного интервала

y=square(2*pi*t/T); % Генерирование прямоугольной %последовательности

Функция y= square(t, duty) генерирует последовательность прямоугольных импульсов с периодом 2π для последовательности отсчетов, определяемой в векторе t, параметр duty задает продолжительность положительной полуволны в процентах от периода

4. Создание единичного импульса delta1=[1] , вычисление свертки delta1 и последовательности sqgen(50, 10).

delta1=[1];

s=sqgen(50,10);

c=conv(delta1,s);

subplot(311), stem(delta1);

title ('delta1=[1]')

subplot(312), stem(s);

title ('Прямоугольная волна')

axis([0, 55, -1.5, 1.5])

subplot(313), stem(c);

title ('Свёртка delta1=[1] и прямоугольной волны')

axis([0, 55, -1.5, 1.5])

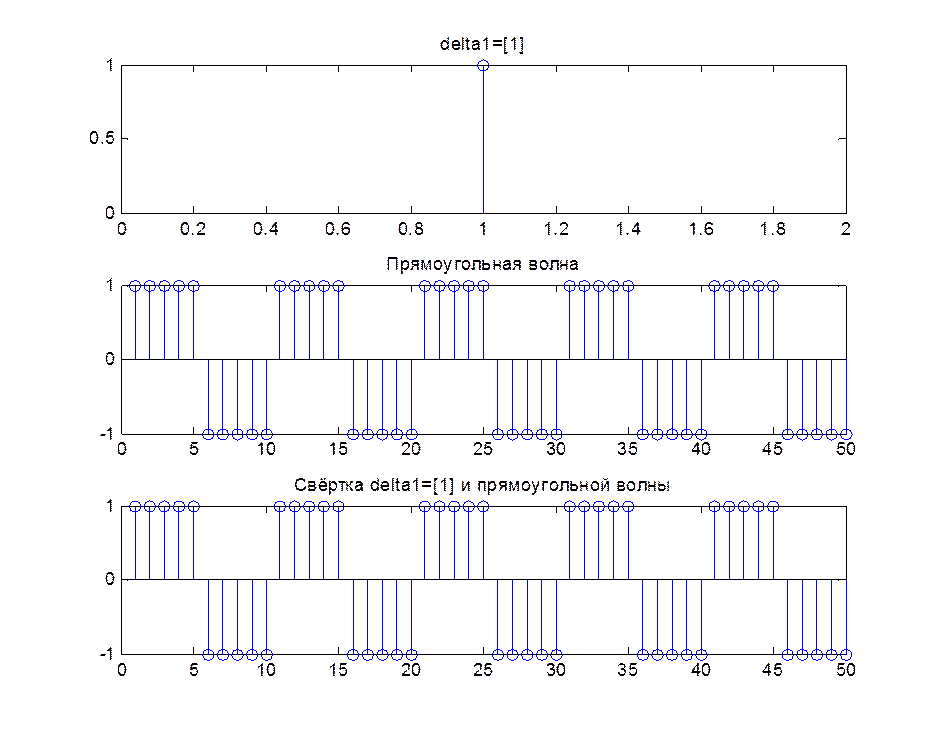
Рис.4. Графическое изображение функции delta=[1] и sqgen(50, 10), и их свертки.

Из графиков видно, что свертка сигналов в точности повторяет сигнал sqgen(50, 10). При каждом n значение свертки определяется как соответствующее значение сигнала sqgen(50, 10), умноженное на единицу; все остальные слагаемые свертки зануляются.

Таким образом, если импульсная характеристика близка к единичной функции, то тогда можно получить исходную функцию.

5. вычисление свертки delta2 и sqgen(50, 10).

delta2=[1 zeros(1,9)]

s=sqgen(50,10);

c=conv(delta2,s);

subplot(311), stem(delta2);

title ('Фунция delta2')

axis([0, 2, 0, 1.5])

subplot(312), stem(s);

title ('Прямоугольная волна')

axis([0, 60, -1.5, 1.5])

subplot(313), stem(c);

title ('Свёртка delta2=[1 zeros(1,9)] и прямоугольной волны')

axis([0, 60, -1.5, 1.5])

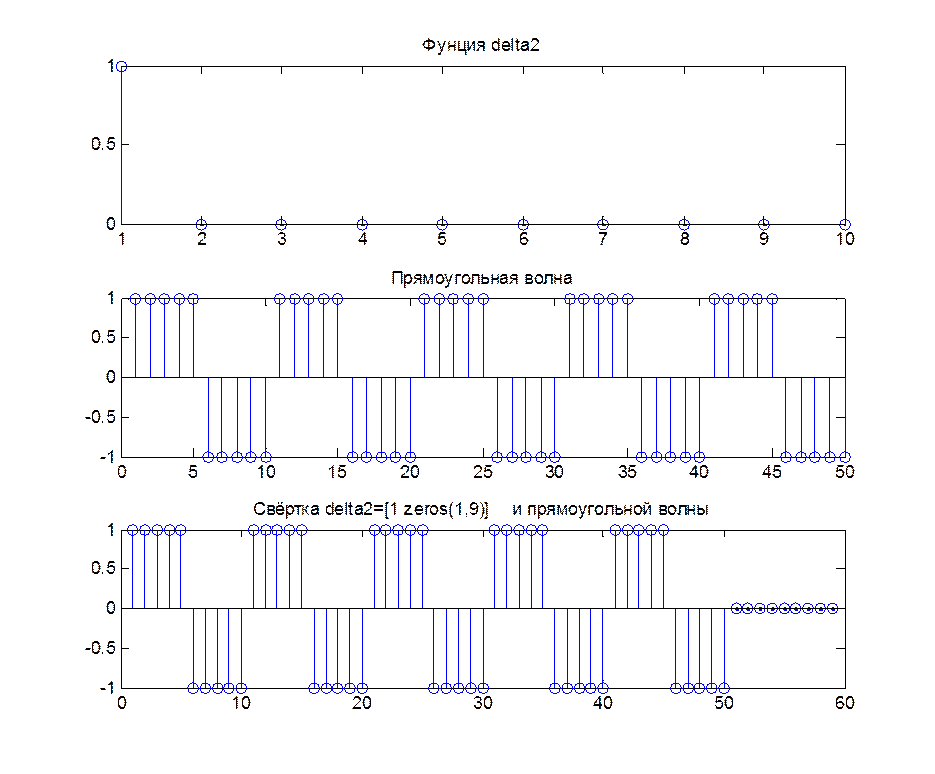
Рис.5. Графическое изображение сигналов delta2=[1 zeros(1,9)] и s=sqgen(50, 10); их свертка.

Свертка любой последовательности и единичной функции будет иметь вид последовательности: 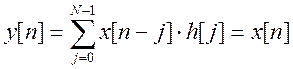, длительность сигнала свертки при этом равен отсчетам. Таким образом, длительность свертки в пункте 4 равен: . В пункте 5 после дополнения дельта-функции нулями j приняло значение, равное 10; таким образом, длительность свертки изменился: 50+10-1=59. Первые 50 отчетов представляют собой сигнал sqgen(50, 10); 9 последних отчетов заполнены нулями, поскольку в первом сигнале со второго по десятый отсчеты - нули