Изучение понятия и свойств непрерывной и дискретной свертки. Вариант 3, страница 2

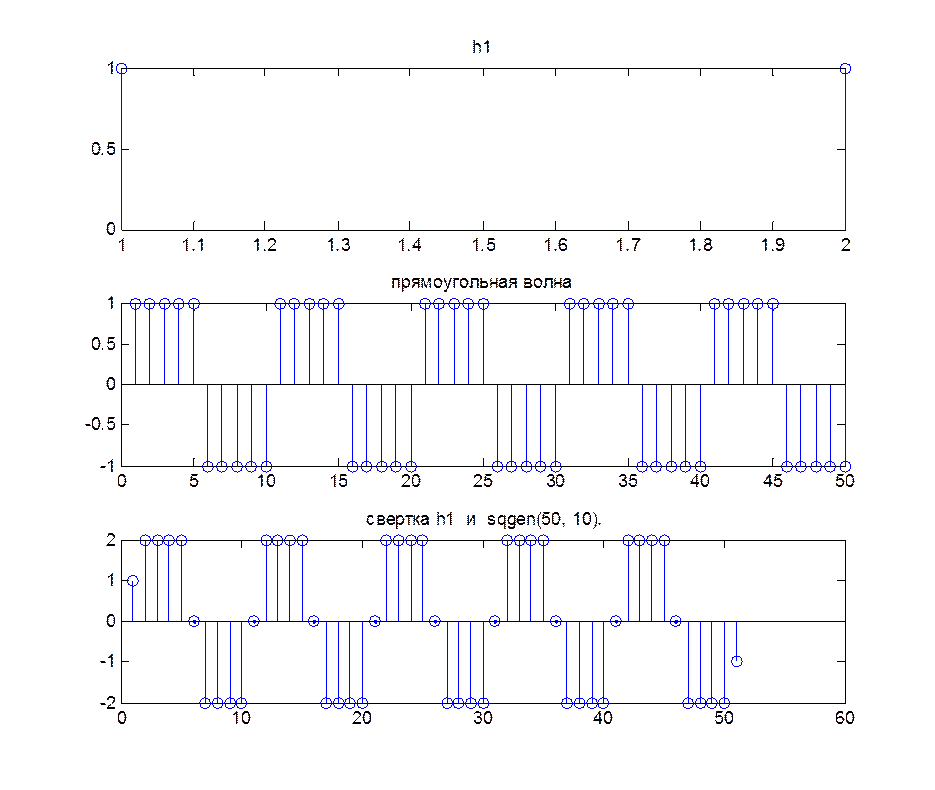
Рис.6. Графическое изображение графиков h1=[ones(1,2)] и sqgen(50, 10), их свертка.

 Длина свертки – 51 отсчет (50+2-1=51).

Увеличение  длины импульса до 8:

h1=[ones(1,8)];

s=sqgen(50, 10);

c=T*conv(h1,s);

subplot(311), stem(h1);

title ('h1')

subplot(312), stem(s);

title ('Прямоугольная волна')

subplot(313), stem(c);

title ('Свертка h1=[ones(1,8)] и sqgen(50, 10)')

Рис.7. Графическое изображение графиков h1=[ones(1,8)] и sqgen(50, 10), их свертка.

Длина свертки – 57 отсчетов (50+8-1=57).

Увеличение длительности одного из сигналов, при сохранении неизменным второй сигнал, форма свертки преобразует фронты, зависящие от длительности сигналов.

7.     Вычисление  обратной свертки сигналов с помощью функции deconv().

Свертка сигналов

                                   

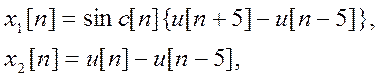
где 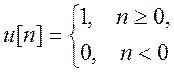     - дискретная единичная ступенчатая функция.

Функция для определения дискретной единичной ступенчатой функции:

function u=fun(t)

for i=1:length(t)

    if t(i)>=0

        u(i)=1;

    end

    if t(i)<0

        u(i)=0;

    end

end

М-файл для генерирования сигналов, вычисления их свертки и восстановления сигнала  из свертки:

T=5;

t=-T:T;                                       %определение временного интервала

tn=0:T;

t1=tn-5;

t2=tn+5;

u=fun(tn);                                  %определение функции u(t)

u1=fun(t1);                                %определение функции u(t-5)

u2=fun(t2);                                %определение функции u(t+5)

figure(1);

subplot(311), stem(tn,u); title('u(t)');

subplot(312), stem(tn,u1); title('u(t-5)');

subplot(313), stem(tn,u2); title('u(t+5)');

t1=0:T;

x1=sinc(t/pi);                                       %определение сигналов

x2=u-u1;

x=conv(x1,x2);                          %вычисление свертки сигналов

figure(2);

subplot(411), stem(t,x1),title('x1');

subplot(412), stem(t1,x2),title('x2');

subplot(413), stem(x), title('Свертка x1 и x2')

x3=deconv(x,x2);  %выделение сигнала х1 из свертки

subplot(414), stem(t,x3), title('Восстановленный сигнал x1')

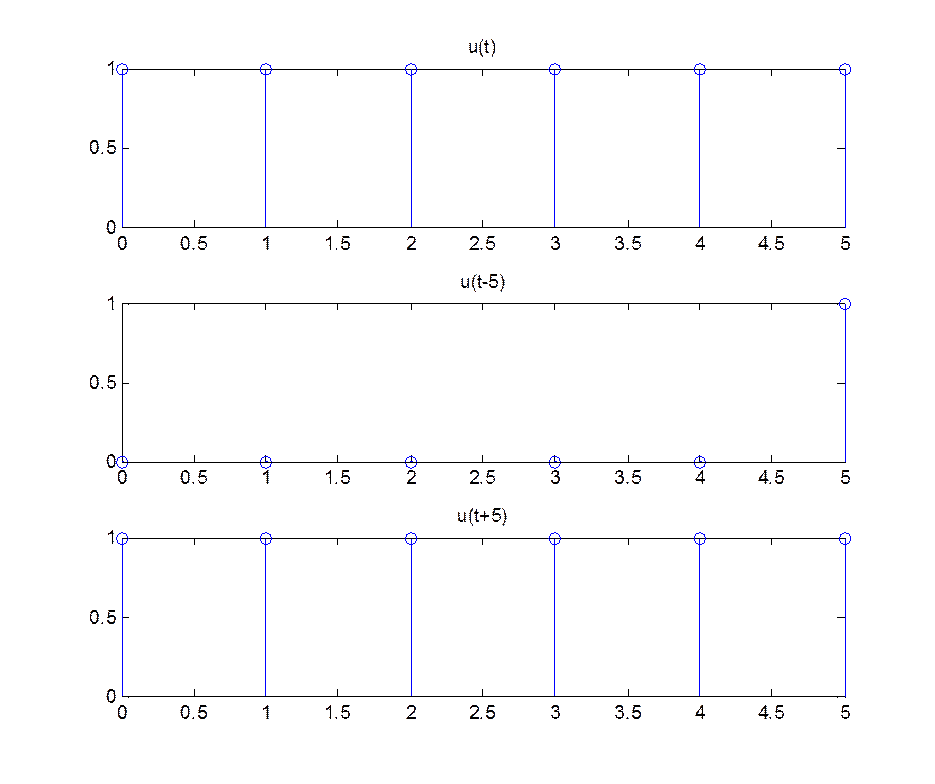
Рис.8.  Графическое изображение сигналов u[n], u[n+5], u[n-5]

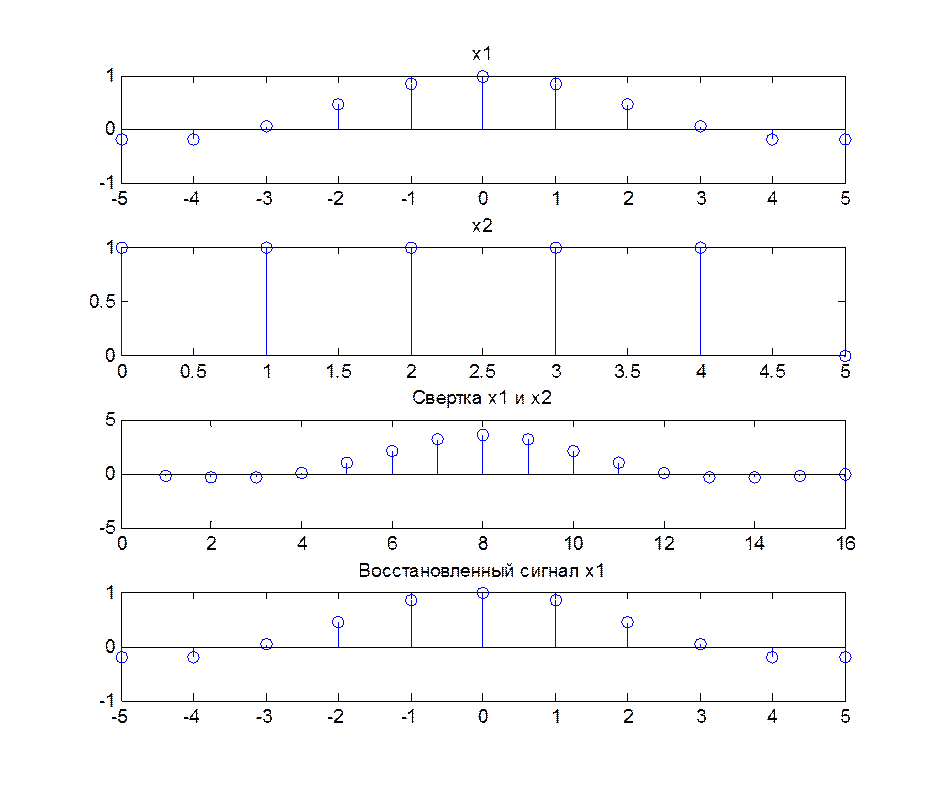
Рис.9.  Графики сигналов x1 и x2, их свертка и сигнал x1, восстановленный

из свертки с помощью функции deconv().

Из построенных графиков видно, что результат функции deconv() в точности совпадает с исходным сигналом х1.

Функция deconv() позволяет выполнять обратную операцию свёртки и тем самым восстанавливать из свёртки один из сигналов, зная другой сигнал. 

На практике с помощью обратной свёртки можно, например, найти импульсную характеристику ЛДС, зная входной и выходной сигналы, т.к. выходной сигнал ЛДС определяется как дискретная свертка входного сигнала  x[n] и импульсной характеристики h[n] системы.

8.  Вычисления свертки в частотной области

Процедура для формирования сигналов и вычисления свертки  через ДПФ

i1 = 0:400;

i2 = 0:199;

x1=exp(-0.01.*i1); % сигнал x1

x2 = ones(1,200) % сигнал  x2

n1=length(x1);

n2=length(x2);

k1=1:(n1+n2-1);

% вычисление  свертки

tic

for  n=1:n1+n2-1,

   y(n)=0;

   for k=max(1,n+1-n1):min(n,n2),

      y(n)=y(n)+sum(x1(n+1-k)*x2(k));

   end

end

t1=toc

subplot(311), plot(i1,x1),title('Сигнал x1')

subplot(312), plot(i2,x2),title('Сигнал x2')

subplot(313), plot(k1,y), title('Свертка x1  и  x2 во временной области')

tic

x3 = [x1 zeros(1,623)];

x4 = [x2 zeros(1,824)];

X1=fft(x3);

X2=fft(x4);

Y=X1.*X2;

yf=ifft(Y);

t2=toc

k = 0:1023;

figure(2)

plot(k,abs(yf));

title('Свёртка сигналов x1 и x2 в частотной области')

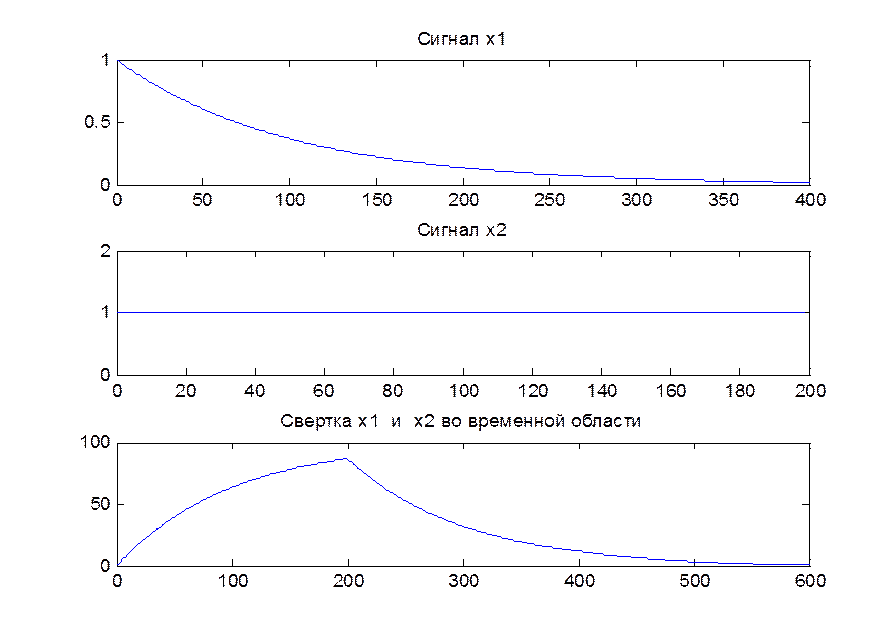
Рис.10. Графики экспоненциального убывающего сигнала длительностью 401 отсчетов  и прямоугольного дискретного сигнала из 200  отсчетов, их  обычная свертка.

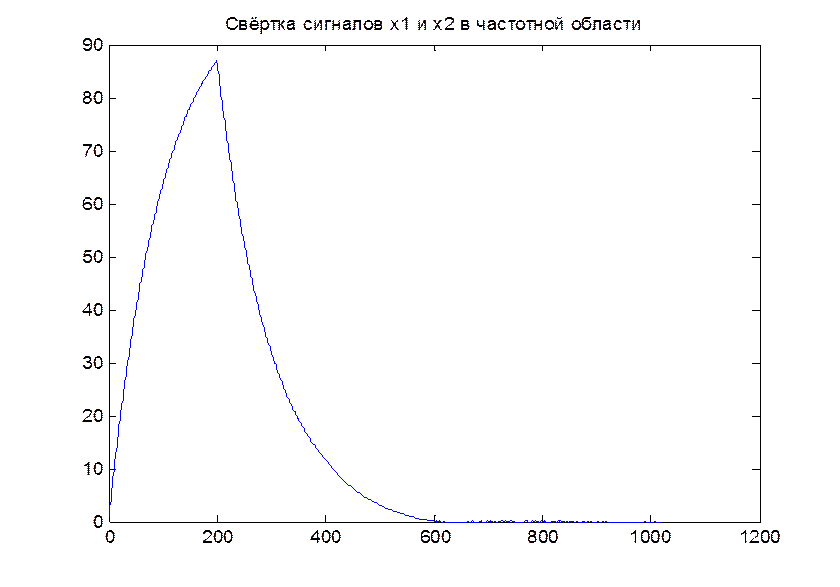
Рис.11. График  свертки  экспоненциального и прямоугольного дискретного  сигналов, вычисленной   в частотной области  с помощью БПФ.

Анализируя графики, видим, что первые 600 отсчетов в точности повторяют свертку во временной области. Следующие 424 отсчета заполнены нулями.

Этот метод вычисления свертки конечных последовательностей называется быстрой сверткой.  Вычисление свертки с помощью БПФ (в частотной области) является более эффективным и быстрым за счет использования быстрых алгоритмов вычисления ДПФ.

t1 = 0.2465с  - время выполнения свертки экспоненциального и прямоугольного дискретного  сигналов во временной области.

t2 =  0.0043с  - время выполнения  свертки этих же сигналов  в частотной области  с помощью БПФ.

Круговая свёртка вычисляется в 57 раз быстрее линейной.

Это объясняется тем, что линейная свертка сигналов длительностью М и N отсчетов  требует приблизительно N*M операций,  а вычисление круговой свёртки с использованием БПФ требует примерно   операций, где L – размер БПФ.

В нашем случае N*M = 400*200 = 80000  и , т.е. круговая свёртка практически в 57 раз быстрее линейной, что совпадает с опытными данными.

Выводы:

1. Непрерывная свёртка определяется выражением

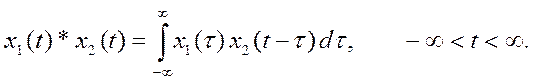
Дискретная свёртка определяется выражением

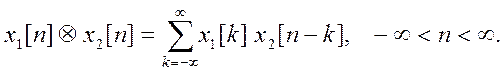
Непрерывную свёртку можно вычислить численным методом с помощью   выражения

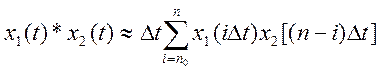, где   - интервал дискретизации.

В п.1 было показано, что результаты вычисления свёртки с помощью   данного выражения совпадают с результатами, полученными с помощью функции conv().

2.  Из п.6. можно сделать вывод, что увеличение длительности одного из сигналов, при сохранении неизменным второй сигнал, форма свертки преобразует фронты, зависящие от длительности сигналов.

3.  В п.8. показали, что использование круговой свёртки в отличие от линейной, позволяет существенно увеличить скорость вычисления (в нашем случае в 57 раз). Это объясняется тем, что линейная свертка сигналов длительностью М и N отсчетов  требует приблизительно N*M операций,  а вычисление круговой свёртки с использованием БПФ требует примерно   операций, где L – размер БПФ.  Но круговая свертка требует дополнения сигналов нулями для избавления  эффекта «перекрытия».

Использованная литература:

1.  Лекция №1 Лекционный курс «Теория и обработка сигналов», доц. Щетинин Ю.И., 2010 г.

2.  Щетинин Ю.И. MATLAB  в  ТОС: Электронное уч. пособие. - Новосибирск. 2004.

3.  Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.:  Уч. пособие.- Новосибирск. Изд-во НГТУ,  1998 - ч.2.