













НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных

Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 8
Z-преобразование и дискретно – временное преобразование Фурье
Группа: АО-41
Вариант: 9 Преподаватель:
Студент: Блохин А.А. доц. Щетинин Ю.И.
2008
Цель работы: изучение Z – преобразования и дискретно – временного преобразования Фурье (ДВПФ), их вычисления в среде Matlab.
Выполнение работы:
1.Z–преобразование и дискретно – временное преобразование Фурье.
Z-преобразование играет важную роль при анализе и проектировании дискретных систем. Так, например, главная характеристика любой цифровой системы - передаточная функция есть отношение Z-преобразований выходного и входного сигнала, также Z-преобразование эффективно используется для решения линейных разностных уравнений с постоянными коэффициентами.
Каузальному сигналу ![]() , т.е. определённому для
, т.е. определённому для ![]() , Z-преобразование
ставит в соответствие функцию комплексной переменной
, Z-преобразование
ставит в соответствие функцию комплексной переменной ![]() :
:
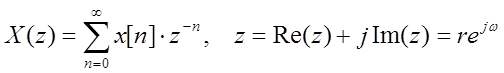 . (1)
. (1)
Формула (1) есть одностороннее прямое Z-преобразование.
Переход от Z-преобразования
![]() к сигналу
к сигналу ![]() во
временной области выполняется с помощью обратного (инверсного) Z-преобразования:
во
временной области выполняется с помощью обратного (инверсного) Z-преобразования:
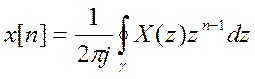 . (2)
. (2)
Здесь интегрирование выполняется по
контуру ![]() , охватывающему все особые точки
(полюса)
, охватывающему все особые точки
(полюса) ![]() . Наряду с прямым вычислением
контурного интеграла для нахождения обратного Z-преобразования
используются также другие способы: разложение Z-преобразования
в степенной ряд и использование разложения Z-преобразования
на простые дроби.
. Наряду с прямым вычислением
контурного интеграла для нахождения обратного Z-преобразования
используются также другие способы: разложение Z-преобразования
в степенной ряд и использование разложения Z-преобразования
на простые дроби.
Таким образом,
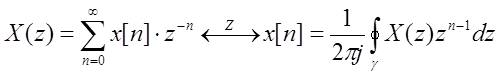 .
.
Если рассматривать ![]() на единичной окружности
(принадлежащей области сходимости Z-преобразования)
в плоскости
на единичной окружности
(принадлежащей области сходимости Z-преобразования)
в плоскости ![]() , где
, где ![]() ,
то формулы прямого (1) и инверсного (2) Z-преобразований
трансформируются в пару выражений ДВПФ:
,
то формулы прямого (1) и инверсного (2) Z-преобразований
трансформируются в пару выражений ДВПФ:
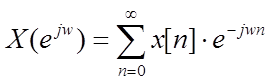 , (3)
, (3)
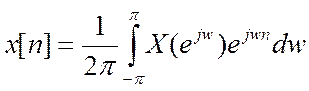 . (4)
. (4)
Формула (3) – прямое ДВПФ, комплексная
функция действительной переменной ![]() . Здесь
дискретному сигналу
. Здесь
дискретному сигналу ![]() ставится в соответствие
непрерывная функция
ставится в соответствие
непрерывная функция ![]() .
.
Формула (4) – обратное ДВПФ. Сигнал ![]() представляется в виде непрерывной
суммы комплексных гармоник с бесконечно малыми амплитудами, пропорциональными
представляется в виде непрерывной
суммы комплексных гармоник с бесконечно малыми амплитудами, пропорциональными ![]() .
.
Таким образом, ДВПФ представляет собой частный случай Z-преобразования на единичной окружности комплексной z-плоскости.
2. Поиск Z–преобразования сигналов
а) ![]() ,
,
б) ![]() ,
,
в) ![]() .
.
а) Z-преобразование сигнала единичного
импульса![]() :
:
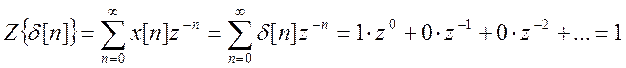
Область сходимости: вся z-плоскость.
б) Z-преобразование
единичной импульсной последовательности![]() :
:
Сумма
бесконечно убывающей геометрической прогрессии (знаменатель ![]() )
) 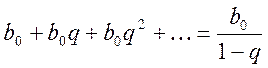 .
.
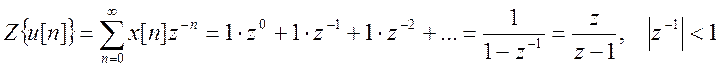 .
.
Полюс
![]() - точка
- точка ![]() .
.
Область
сходимости: ![]() - внешность окружности единичного
радиуса.
- внешность окружности единичного
радиуса.
в) Z-преобразование
дискретного косинуса ![]() :
:
По формуле
Эйлера: 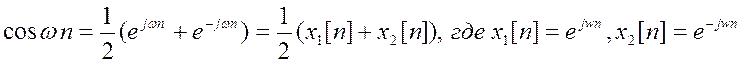

Проводя
аналогичные рассуждения можно получить, что если ![]() (
(![]() ), то Z-преобразование:
), то Z-преобразование:
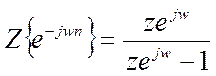
Согласно
свойству линейности Z-преобразования: ![]() ,
тогда
,
тогда
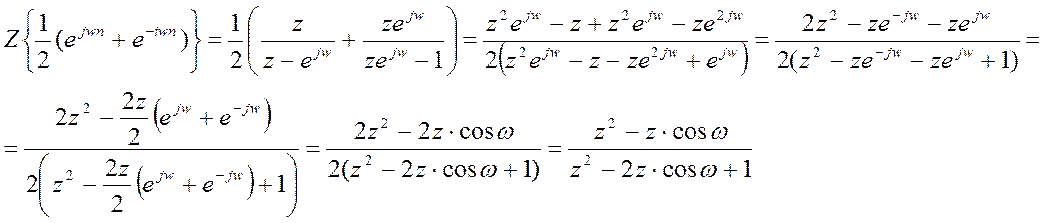
Область
сходимости: ![]() - внешность окружности единичного
радиуса.
- внешность окружности единичного
радиуса.
Комментарий: Как видно из расчётов, Z-преобразование единичного импульса есть
точка на z-плоскости: ![]() ,
т.к. функция
,
т.к. функция ![]() не зависит от комплексной переменной
не зависит от комплексной переменной
![]() , то совершенно очевидно, что
областью сходимости (область, где Z-преобразование
сходится) будет являться вся z-плоскость. Для единичной импульсной
последовательности и дискретного косинуса, очевидно, что степенные ряды будут
сходиться (а, следовательно, и Z-преобразование будет существовать)
только в том случае, если
, то совершенно очевидно, что
областью сходимости (область, где Z-преобразование
сходится) будет являться вся z-плоскость. Для единичной импульсной
последовательности и дискретного косинуса, очевидно, что степенные ряды будут
сходиться (а, следовательно, и Z-преобразование будет существовать)
только в том случае, если ![]() , т.е. областью
сходимости для них будет являться внешность окружности единичного радиуса.
Таким образом, можно сделать вывод, что Z-преобразование
сигнала необходимо рассматривать только вместе с его областью сходимости.
, т.е. областью
сходимости для них будет являться внешность окружности единичного радиуса.
Таким образом, можно сделать вывод, что Z-преобразование
сигнала необходимо рассматривать только вместе с его областью сходимости.
3. Поиск Z-преобразования сигналов с помощью функции ztrans().
а) ![]() ,
,
б) ![]() ,
,
в) ![]() .
.
![]() - вычисляет Z–преобразование символьной функции
- вычисляет Z–преобразование символьной функции![]() .
.
а) Z-преобразование
последовательности ![]() :
:
syms a w n
X=ztrans(a.^n*cos(w*n))
X =(z/a-cos(w))*z/a/(z^2/a^2-2*z/a*cos(w)+1)
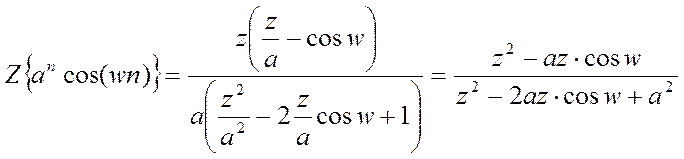
б) Z-преобразование
последовательности ![]() :
:
syms n
y=ztrans(n.^2*exp(2*n))
y =z*exp(2)*(z+exp(2))/(z-exp(2))^3
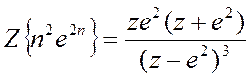
в) Z-преобразование
последовательности ![]() :
:
syms n
y= ztrans(cos(n).^2)
y=(z^2+z-3*z*cos(1)^2+cos(1)^2)*z/(z^3+z^2-4*z^2*cos(1)^2-z+4*z*cos(1)^2-1)
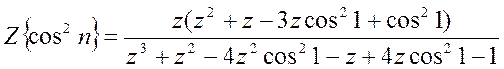
Комментарий: Matlabявляется мощным инструментом для вычисления Z-преобразований.
4. Определение сигналов во временной области по их Z-преобразованию с использованием функции iztrans().
а) 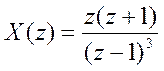
б) 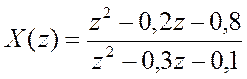
![]() - вычисляет функцию
- вычисляет функцию![]() из Z–преобразования этой функции.
из Z–преобразования этой функции.
а) Сигнал, имеющий Z-преобразование 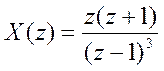 :
:
syms z
y= iztrans(z*(z+1)/(z-1).^3)
y =n^2
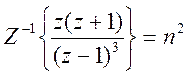
б) Сигнал, имеющий Z-преобразование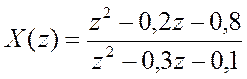 :
:
syms z
y= iztrans((z.^2-0.2*z-0.8)/(z.^2-0.3*z-0.1))
ans =8*charfcn[0](n)-36/7*(-1/5)^n-13/7*(1/2)^n
charfcn[0] – единичный импульс, где ненулевое значение только в точке равной нулю.
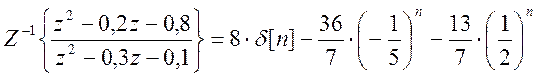
Комментарий: Средства Matlab позволяют также получить обратное Z-преобразование, т.е. вид сигнала во временной области.
5. Обратное Z-преобразование разложением на простейшие дроби.
Z-преобразование имеет вид: 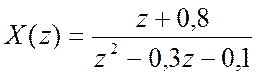 .
.
Функция
![]() выполняет разложение на простые
дроби рациональной Z-функции с вектором коэффициентов
полинома числителя num и вектора коэффициентов полинома
знаменателя den. Результат функции: r – вектор вычетов, p – вектор полюсов, k – вектор коэффициентов целой части
разложения.
выполняет разложение на простые
дроби рациональной Z-функции с вектором коэффициентов
полинома числителя num и вектора коэффициентов полинома
знаменателя den. Результат функции: r – вектор вычетов, p – вектор полюсов, k – вектор коэффициентов целой части
разложения.
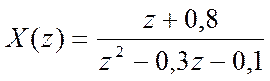
num = [0,1,0.8];
den = [1,-0.3,-0.1];
[r,p,k] = residuez(num,den)
r = 3.7143 p = 0.5000 k = -8
4.2857 -0.2000
Полученному результату отвечает разложение на простые дроби вида
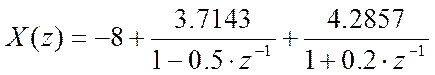
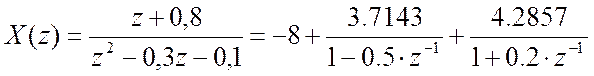
Поскольку
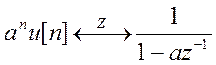 , то
, то 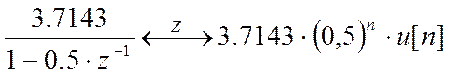 и
и
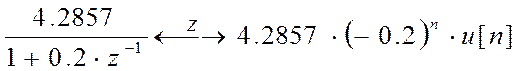 , а т.к.
, а т.к. ![]() ,
то
,
то ![]() .
.
Таким
образом, обратное Z-преобразование: ![]() .
.
Комментарий: Функция комплексной переменной ![]() очень часто имеет вид рациональной
функции вида:
очень часто имеет вид рациональной
функции вида: 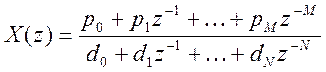 . В данном случае порядок
многочлена числителя не равен порядку многочлена знаменателя (
. В данном случае порядок
многочлена числителя не равен порядку многочлена знаменателя (![]() ,
,![]() ), т.е.
), т.е. ![]() представляет
собой правильную дробь. Каждый член разложения на простейшие дроби вида
представляет
собой правильную дробь. Каждый член разложения на простейшие дроби вида  даёт во временной области
составляющую
даёт во временной области
составляющую ![]() , а постоянная составляющая
, а постоянная составляющая
![]() -
- ![]() .
Воспользовавшись свойством линейности Z-преобразования,
получается искомая последовательность. Метод разложения на простые дроби по
сравнению с непосредственным вычислением контурного интеграла чаще всего
оказывается более удобным и эффективным способом для вычисления обратного Z-преобразования от
.
Воспользовавшись свойством линейности Z-преобразования,
получается искомая последовательность. Метод разложения на простые дроби по
сравнению с непосредственным вычислением контурного интеграла чаще всего
оказывается более удобным и эффективным способом для вычисления обратного Z-преобразования от ![]() , представляющей собой рациональную
дробь.
, представляющей собой рациональную
дробь.
Линейное
разностное уравнение имеет вид: ![]()
Беря Z-преобразование от уравнения, с учётом
свойства временного сдвига: 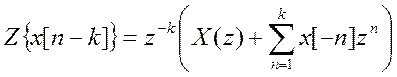 получается:
получается:
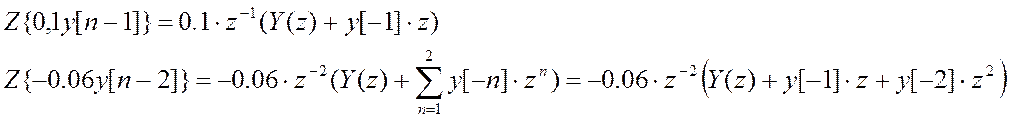
Z-преобразование входного сигнала: ![]()
Решение в Z-области (с учётом начальных условий ![]() ):
): 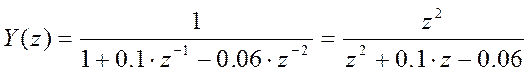
Для вычисления
обратного Z-преобразования от ![]() применяется метод разложения на
простые дроби.
применяется метод разложения на
простые дроби.
Воспользуемся функцией residuez:
num = [1,0,0];
den = [1,-0.1,-0.06];
[r,p,k] = residuez(num,den)
r =
0.6000
0.4000
p =
0.3000
-0.2000
k =[]
Разложение на простые дроби имеет вид:
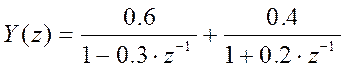
Обратные Z-преобразования:
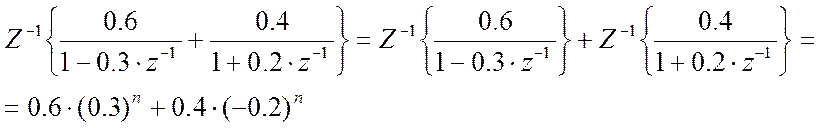
Решение уравнения во временной области имеет вид:
![]()
Комментарий: Как видно из примера, одной из областей применения Z-преобразования на практике является решение линейных разностных уравнений. При этом алгоритмом решения будет являться:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.