Вычисление прямого и обратного Z – преобразования в MatLab
1. Прямое Z – преобразование
Функция X=ztrans(x) вычисляет Z – преобразование символьной функции x
Пример.
» syms X x r w0 n
» x=r^n*(cos(w0*n));
» X=ztrans(x)
X =
-z*(cos(w0)*r-z)/(r^2-2*z*cos(w0)*r+z^2)
2. Обратное Z – преобразование
Синтаксис x = iztrans(X)
Пример
» syms z x X
» X=2*z/(z-2)^2;
» x=iztrans(X)
x =
2^n*n
3. Функция [z, p, k] = tf2zp(num, den)
Определяет нули z, полюса p и коэффициент усиления k по значениям векторов коэффициентов полинома числителя num и знаменателя den.
Пример. Пусть 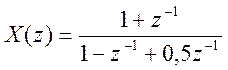 .
.
» num =[1, 1];
» den = [1, -1, 0.5];
» [z, p, k]=tf2zp(num,den)
z =
-1
p =
5.0000e-001 +5.0000e-001i
5.0000e-001 -5.0000e-001i
k =
1
Функция [num, den] = zp2tf(z, p, k) выполняет обратное преобразование.
4. Функция zplane(zeros, poles) строит график нулей и полюсов рациональной дроби X(z). В этой функции zeros – вектор нулей, poles – вектор полюсов.
Аналогично zplane(num, den) строит тот же график по векторам коэффициентов полиномов num, den.
Пример. 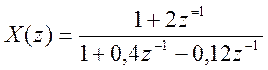 .
.
» num=[1, 2];
» den = [1, 0.4, -0.12];
» zplane(num, den)
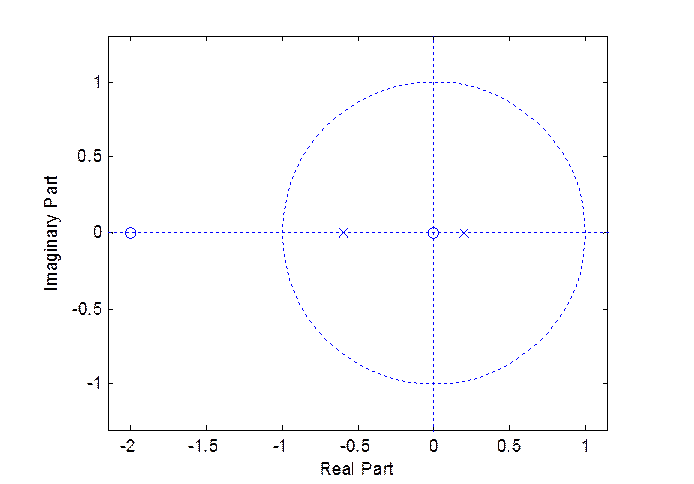
5. Функция [r, p, k]=residuez(num, den) выполняет разложение на простейшие дроби рациональной Z- функции с вектором коэффициентов полинома числителя num и вектора коэффициентов полинома знаменателя den. Результат функции: r – вектор вычетов, p – вектор полюсов, k – вектор коэффициентов целой части разложения.
Пример. 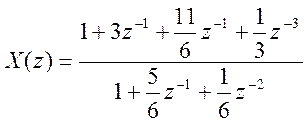 .
.
» num=[1,3,11/6,1/3];
» den=[1,5/6,1/6];
» [r, p, k]=residuez(num, den)
r =
-1.0000e+000
1.0000e+000
p =
-5.0000e-001
-3.3333e-001
k =
1 2
Полученному результату отвечает разложение на простейшие дроби вида
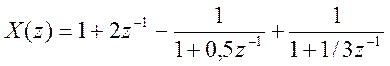
6. Функция [num, den] = residuez(r, p, k) осуществляет обратное преобразование разложения на простейшие дроби в рациональную дробь с коэффициентами числителя num и знаменателя den.
7. Функция imp(z) может быть использована для вычисления обратного
Z – преобразования с помощью
разложения X(z)
в степенной ряд.
Синтаксис [h, n] = imp(b, a, n), h - вектор отсчетов, n – номера отсчетов, b и а – коэффициенты многочленов числителя и знаменателя X(z)
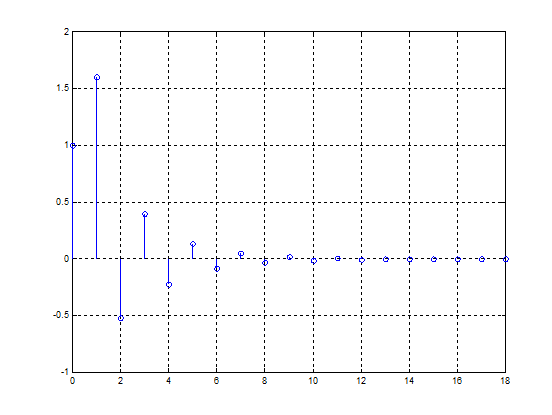
Пример. 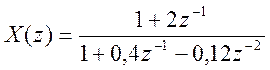
» b=[1 2];
» a=[1 0.4 -0.12];
» [h,n]=impz(b,a);
» stem(n,h)
» grid
Составил: доц. Щетинин Ю.И.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.