Министерство образования и науки Российской Федерации
Новосибирский государственный технический университет
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Лабораторная работа № 1
НЕПРЕРЫВНЫЕ И ДИСКРЕТНЫЕ
ПО ВРЕМЕНИ СИГНАЛЫ
Факультет: АВТ Преподаватель:
доц. Щетинин Ю.И.
Группа: АИ-72 Преподаватель: Щетинин Ю.И.
Студент: Спитченко В.М.
Новосибирск
2009
Цель работы: Знакомство со средой MATLAB, приобретение практических навыков генерирования непрерывных и дискретных по времени сигналов, построения графиков сигналов в среде MATLAB.
1. Построение графика непрерывного по времени гармонического сигнала.
С помощью следующей последовательности команд построим график непрерывного по времени гармонического сигнала.
A=10;
f=50;
phi=pi/5;
t=0:0.0005:0.04;
%массив (время отсчетов) от нуля до 4-х с шагом 0.0005
y=A*sin(2*pi*f*t-pi/5);
plot(t,y,'ro-')
% параметры: ro- параметры вывода графика (цвет (к- %красный) o – окружность “-” сплошная линия)
grid %Нанесли сетку
set(gca,'FontName','Arial Cyr', 'FontSize',10)
%устанавливаем свойства объекту «текст %заголовка» -
%шрифт и размер
title('График гармоники') %Выводим заголовок
xlabel('t, c')%подписываем оси координат
ylabel('y(t)')
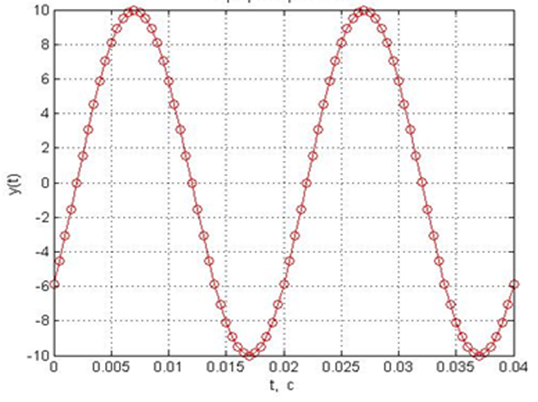
Рис.1. График гармоники.
Определим параметры гармоники:
1. Амплитуда. A = 10 В
2. Частота. f = 50 Гц
3. Период. T = 0.02 с
4. Начальная
фаза. ![]() =
= ![]() °
°
5. Мощность. P = 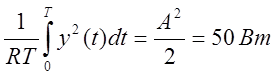
2. Построение графиков дискретных по времени сигналов.
С помощью следующей последовательности команд построим график дискретного по времени гармонического сигнала.
n = 0 : 1 : 30; %массив отсчетов n от
1 до 30 с шагом 1
y = sin(n/3); %новый массив, в который помещается результат выполнения
функции y = sin(n/3) – функция берёт аргументы из массива n
subplot(3,1,1);
stem(n, y);
% Команда stem(x, y) выводит график элементов массива y в виде вертикальных линий в позициях, определяемых массивом x, элементы которого должны быть упорядочены в порядке возрастания.
xlabel('n')
ylabel('y(n)')
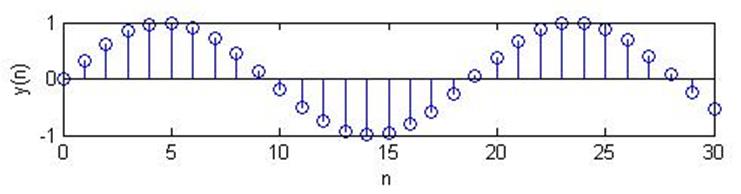
Рис.2. Дискретный гармонический сигнал
С помощью следующей последовательности команд построим график четырёх периодов дискретной по времени гармоники с частотой 100 Гц, частотой отсчетов
1000 Гц и начальной фазой π/2.
f=100;
Fs=1000;
t = 0 : 1/Fs : 4/f;
y = sin(2*pi*f*t + pi/2);
stem(t, y)
set(gca,'FontName','Arial Cyr', 'FontSize',10)
title('График дискретной гармоники')
xlabel('t')
ylabel('y(t)')
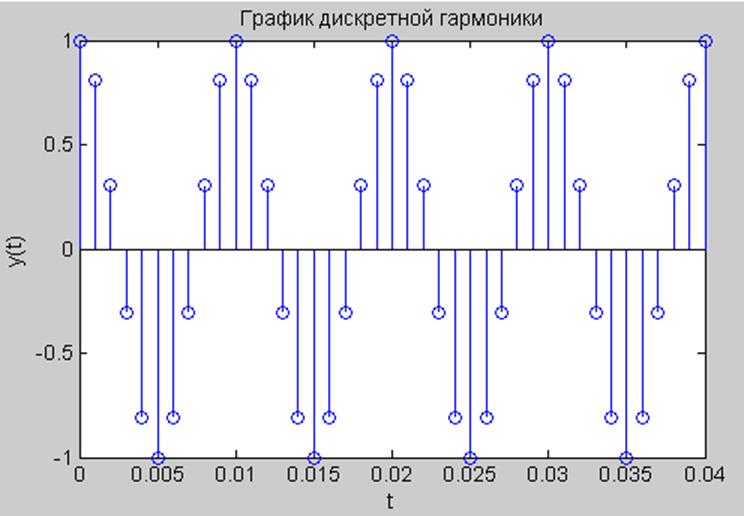
Рис 3. График дискретной гармоники
Вывод:
Дискретный по времени сигнал задаётся на счетном множестве точек аргумента и может принимать действительные или комплексные значения.
Непрерывный по времени сигнал – сигнал, определённый на несчетном множестве значений аргумента.
Для построения графиков в среде matlab используются функции plot (для непрерывных) и stem (для дискретных).
3. Построение графика комплексной экспоненты.
С помощью
следующей последовательности команд построим график комплексной экспоненты ![]() с показателем затухания σ = -
0, 0693 и периодом Т = 2 секунды.
с показателем затухания σ = -
0, 0693 и периодом Т = 2 секунды.
t = 0 : 10/500 : 10;
sigma = -0.0693;
T=2;
y = exp((sigma+j*2*pi/T)*t);
plot(y)
set(gca,'FontName','Arial Cyr', 'FontSize',10)
xlabel('Im(y)');
ylabel('Re(y)');
title('График комплексной экспоненты ')
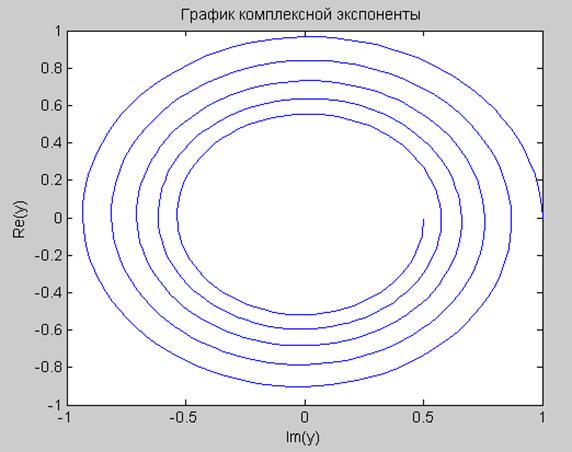
Рис 4. График комплексной экспоненты
Построим графики модуля, аргумента действительной и мнимой частей комплексной экспоненты.
Последовательность команд:
t=0:10/500:10;
sigma=-0.693;
T=2;
set(gca,'FontName','Arial Cyr', 'FontSize',10);
y = exp((sigma+j*(2*pi/T))*t);
subplot(2,2,1);
plot(t,abs(y));
ylabel('Re(y(t))');
title('График действительной части экспоненты');
subplot(2,2,2);
plot(t,imag(y));
xlabel('t');
ylabel('Im(t)');
title('График мнимой части экспоненты');
subplot(2,2,3);
plot(t,abs(y));
ylabel('abs(y)');
title('График модуля экспоненты');
subplot(2,2,4);
plot(t,angle(y));
xlabel('t');
ylabel(' angle (y)');
title('График аргумента экспоненты');
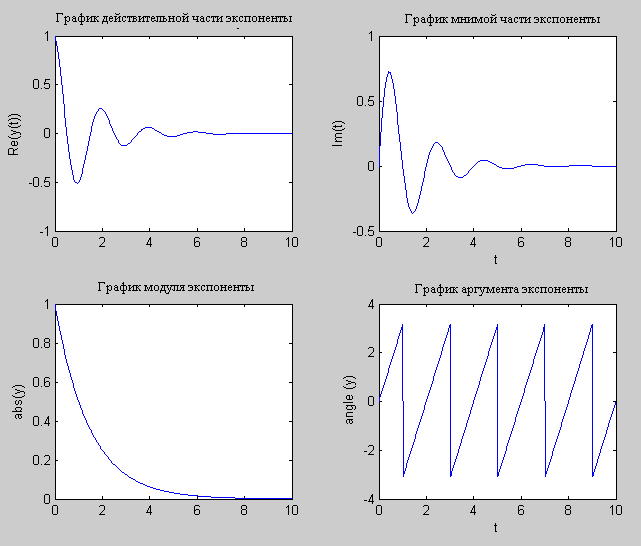
Рис.4
Графики действительной, мнимой
частей и модуля комплексной гармоники
Выводы:
· Модуль комплексной гармоники имеет вид экспоненты
· Мнимая и действительная части комплексной гармоники имеют вид затухающей гармонической функции (коэффициент затухания σ = -0,0693)
· Аргумент комплексной гармоники – имеет вид линейной периодической функции
4. Формирование прямоугольных и треугольных импульсов.
Построим в одном графическом окне графики сигналов:
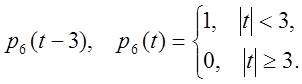 и
и ![]() ,
где
,
где ![]() - прямоугольный импульс
длительностью шесть единиц и
- прямоугольный импульс
длительностью шесть единиц и ![]() - треугольный
импульс с основанием четыре единицы и единичной высотой, смещенный на три
единицы по оси аргумента.
- треугольный
импульс с основанием четыре единицы и единичной высотой, смещенный на три
единицы по оси аргумента.
Прямоугольный импульс
Последовательность команд
t=-5:0.01:10;
tau=6;
p=rectpuls(t-3,tau);
plot(t,p);
axis([-5,10,-5,5]);
xlabel('t');
ylabel('p');
grid();
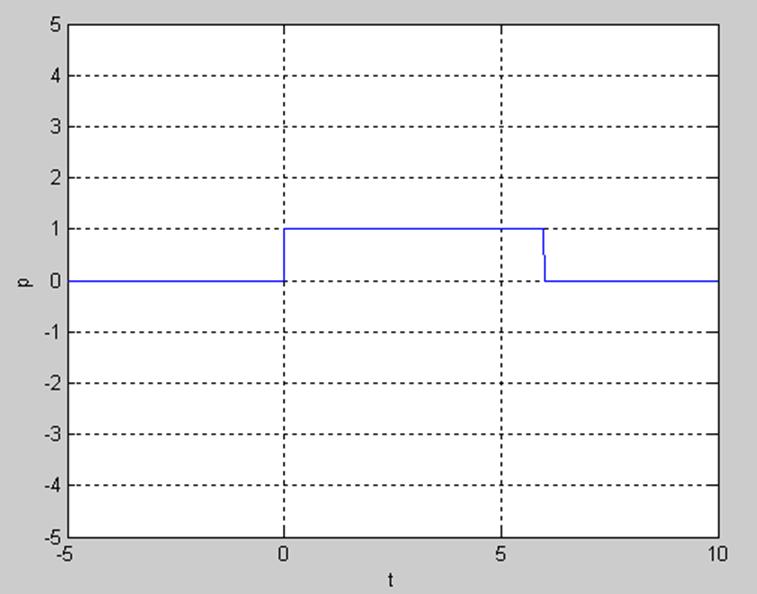
Рис.5
Прямоугольный импульс 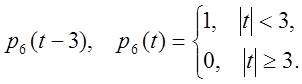
Треугольный импульс
Последовательность команд
t=-0:0.01:8;
tau=6;
p=tripuls(t-3,4);
plot(t,p);
axis([-10,10,-2,2]);
xlabel('t');
ylabel('p');
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.