Дискретное и быстрое преобразования Фурье: Методические рекомендации по выполнению лабораторной работы

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

«Теория  и  обработка  сигналов»

ЛАБОРАТОРНАЯ  РАБОТА  № 4

ДИСКРЕТНОЕ И БЫСТРОЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ

Вариант 8

Факультет:  АВТ                                       Преподаватель:

Группа:         АО-21                                   Щетинин Ю. И.

Студент:       Минин Ю. В.                          

Новосибирск

2004

Цель работы:Изучение дискретного преобразования Фурье и его свойств, алгоритмов быстрого преобразования Фурье. Приобретение практических навыков вычисления и использования дискретного преобразования Фурье в среде Matlab.

Задание №1:Используем  функцию dftsum() для вычисления ДПФ по выражению

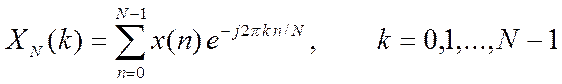      ,            вычислить ДПФ

следующих сигналов:

а)    для  N = 10.

а)  x(n) = 1 для N = 10,

б)  x(n) = cos(2πn/10) для  N = 10.

Построим графики амплитудных спектров для каждого случая.

Напишем функцию (.m - файл)  для вычисления дискретного преобразования Фурье:

function X=dftsum(x); % определение функции dftsum(x)

N=length(x); % вычисление количества точек, рассчитанных для исходного         

              % сигнала  x   

for n=0:1:N-1;

   for k=0:1:N-1;

      xk(k+1)=x(k+1)*exp(-j*2*pi*k*n./N); % формула для вычисления ДПФ

   end

   X(n+1)=sum(xk);

end;

Файл-сценарий для вычисления ДПФ сигнала:

  для N = 10:

T=10;

t=-T/2:T/2-1; %определение временного интервала

for i=1:T %определение сигнала

    if t(i)==0,

    d1(i)=1;

else

    d1(i)=0;

end

end

y=dftsum(d1); y1p=fftshift(y);  % вычисление  ДПФ

% Построение графиков сигнала и его амплитудного спектрa

figure,

subplot(211), stem(t,d1)

subplot(212), stem(t,abs(y1p)),title('Амлитудный спектр')

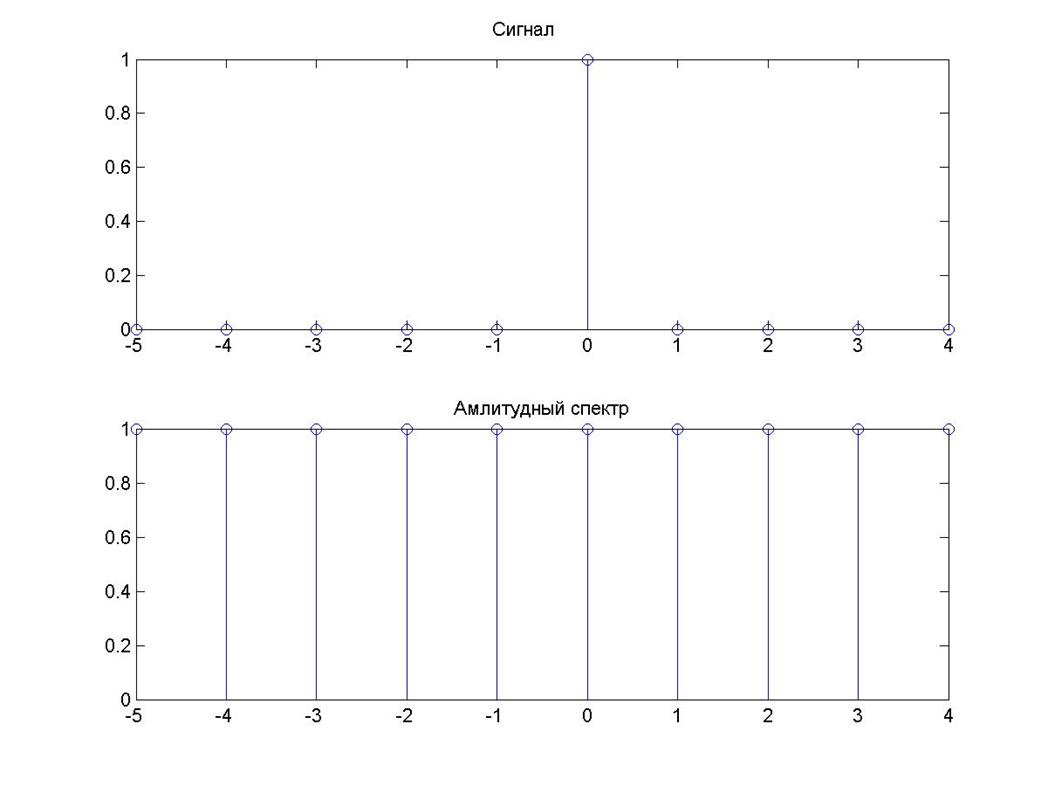
Рис. 1

Амплитудный спектр дельта - функции  представляет собой единичную последовательность.

Файл-сценарий для вычисления ДПФ сигнала x(n) = 1 для N = 10:

T=10

t=-T/2:T/2-1; %определение временного интервала

for i=1:T

    d2(i)=1; %определение сигнала

end

y=dftsum(d2); y1p=fftshift(y); % вычисление и сдвиг ДПФ

% Построение графиков сигнала и его спектров

figure,

subplot(211), stem(t,d2)

subplot(212), stem(t,abs(y1p)),title('Амлитудный спектр')

 

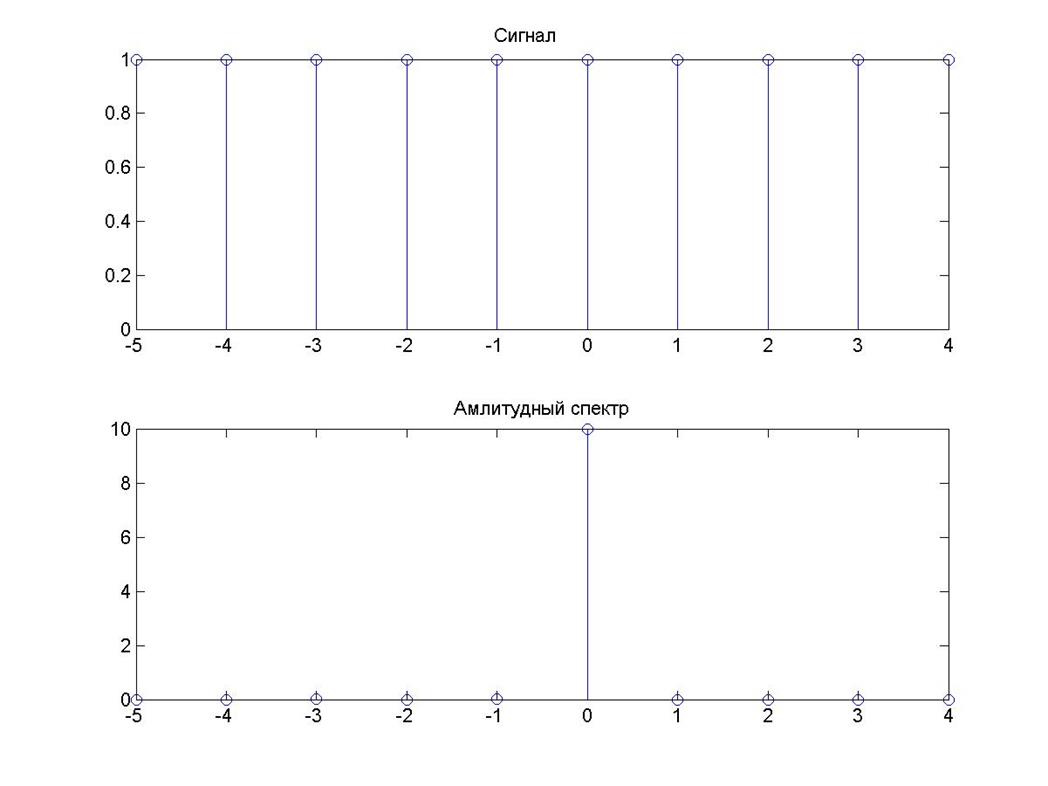
 Рис. 2

Амплитудный спектр единичного сигнала представляет собой дельта - функцию.

Файл-сценарий для вычисления ДПФ сигнала x(n) = cos(2πn/10)  для N = 10:

T=10;

t=0:T-1; %определение временного интервала

d3=cos(2*pi*t/10); %определение сигнала

y=dftsum(d3); y1p=fftshift(y); % вычисление и сдвиг ДПФ

% Построение графиков сигнала и его спектров

figure,

subplot(211), stem(t,d3)

subplot(212), stem(t,abs(y1p)),title('Амлитудный спектр')

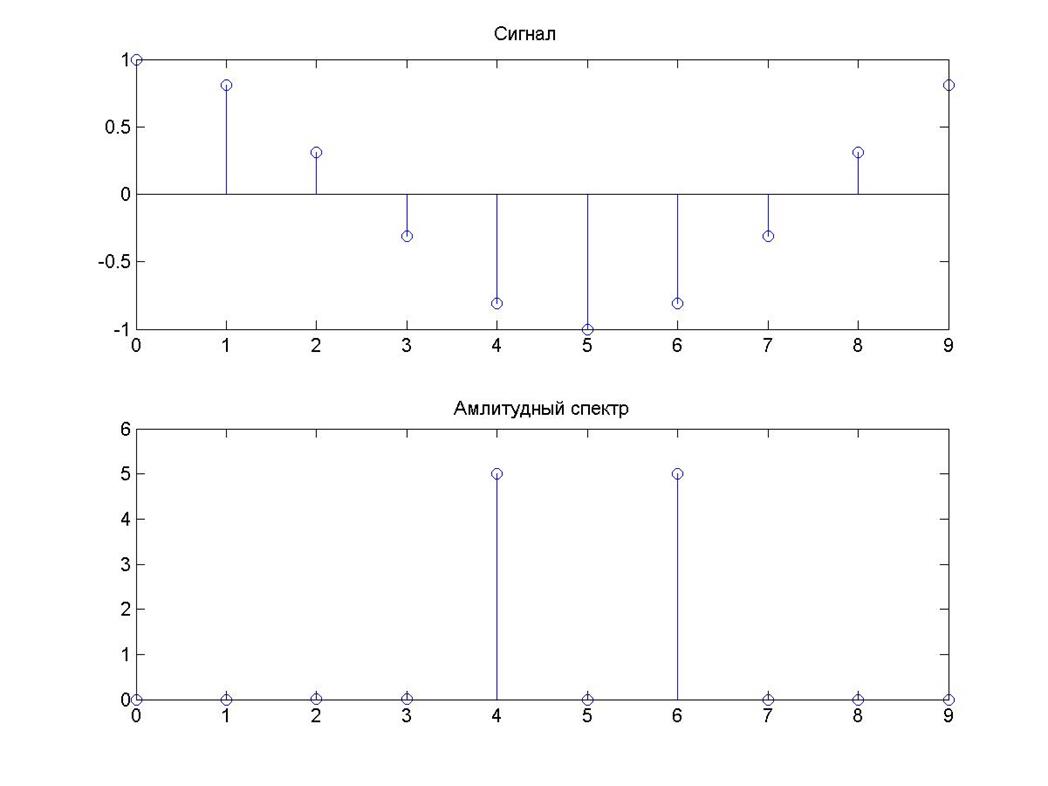
Рис. 3

Амплитудный спектр сигнала x(n) = cos(2πn/10) представляет собой две дельта – функции.

Задание №2:Напишем Matlab-функцию для вычисления обратного (инверсного)  ДПФ   с форматом x = idftsum(X). Формула вычисления этого  преобразования:

                        ,                       

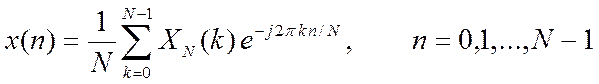Применим написанную функцию idftsum(X) для вычисления  обратного  ДПФ  сигналов,рассмотренных выше. Сопоставим графики исходных  сигналов и результаты вычисления с помощью idftsum(X).

Функция idftsum() для вычисления ОДПФ:

function Y=idftsum(x);  % определение функции idftsum(x)

N=length(x);      % вычисление размера вектора  x

for n=0:N-1;

   for k=0:N-1;

      Yk(k+1)=x(k+1)*exp(j*2*pi*k*n./N);% формула для вычисления

                                        % ОДПФ

end

   Y(n+1)=abs(sum(Yk)/N);

еnd

Для устранения мнимой части, которая может возникнуть из-за ошибок округления, применяется функцию abs(x).

Для вычисления ОДПФ к результатам выполнения функции dftsum(X) применим функцию idftsum(X).

М-файл для вычисления ОДПФ сигнала :

T=10;

t=-T/2:T/2-1;

for i=1:T

    if t(i)==0,

    d1(i)=1;

else

    d1(i)=0;

end

end

x=dftsum(d1); % вычисление  ДПФ

y=idftsum(x);  % вычисление  ОДПФ

% Построение графиков сигнала и его амплитудного спектра

figure,

subplot(311), stem(t,d1), title('Исходный сигнал')

subplot(312), stem(t,abs(x)),title('Амлитудный спектр')

subplot(313), stem(t,y), title('ОДПФ сигнала')

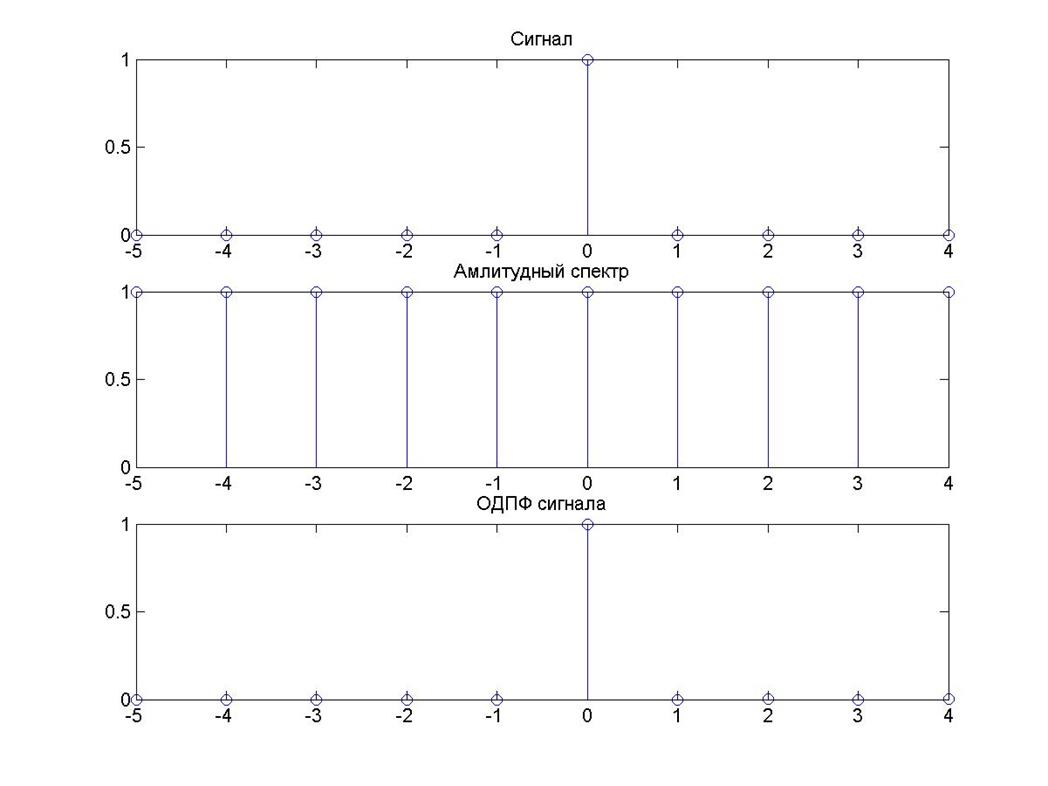
Рис. 4

М-файл для вычисления ОДПФ сигнала x(n) = 1:

T=10;

t=-T/2:T/2-1; %определение временного интервала

for i=1:T

    d2(i)=1; %определение сигнала

end

x=dftsum(d2); x1p=fftshift(x); % вычисление и сдвиг ДПФ

y=idftsum(x1p); % вычисление  ОДПФ

% Построение графиков сигнала и его спектров

figure,

subplot(311), stem(t,d2),title('Исходный сигнал')

subplot(312), stem(t,abs(x1p)),title('Амлитудный спектр')

subplot(313), stem(t,y), title('ОДПФ сигнала')

Результат выполнения:

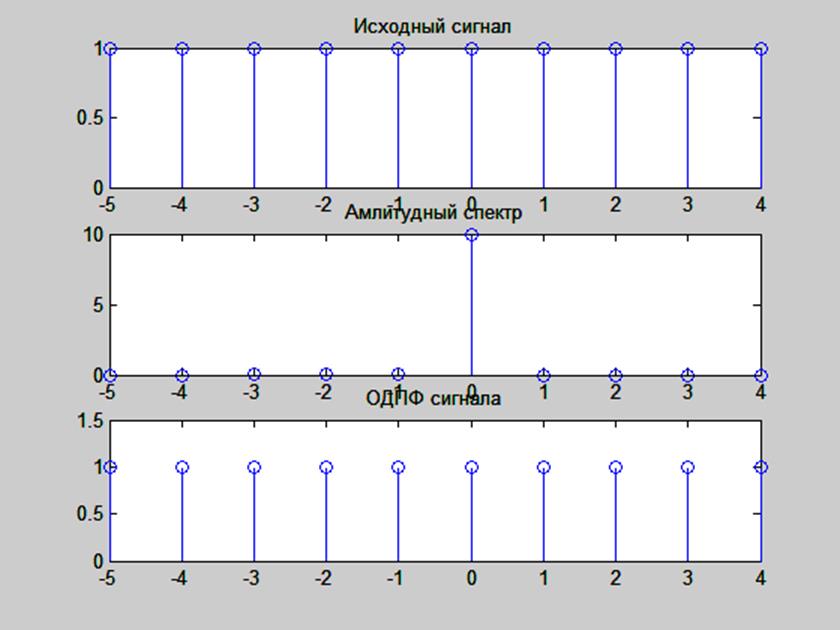
Рис. 5.  Графики сигнала x(n) = 1, его ДПФ и ОДПФ

По построенным графикам видно, что исходные сигналы и их обратное ДПФ совпадают для двух рассмотренных случаев.

М-файл для вычисления ОДПФ сигнала x(n) = cos(2πn/10):

T=10;

t=0:T-1;

d3=cos(2*pi*t/10);

x=dftsum(d3); x1p=fftshift(x); % вычисление и сдвиг ДПФ

y=idftsum(x1p); % вычисление  ОДПФ

% Построение графиков сигнала и его спектров

figure,

subplot(311), stem(t,d3),title('Исходный сигнал')

subplot(312), stem(t,abs(y1p)),title('Амлитудный спектр')

subplot(313), stem(t,y), title('ОДПФ сигнала')

Результат выполнения:

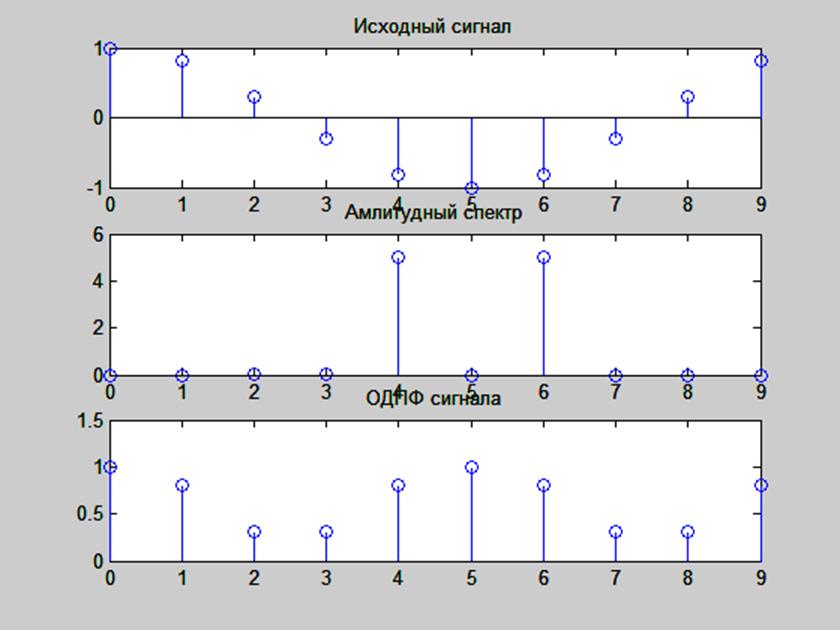
Рис. 6. Графики сигнала x(n) = cos(2πn/10), его ДПФ и ОДПФ

Поскольку  в функции idftsum(x) для устранения мнимой части используется функция abs(), то график ОДПФ данного сигнала представляет собой модуль исходного сигнала. По остальным критериям также наблюдается соответствие.

1.  Вычислить с помощью функции dftsum(x)  ДПФ случайной   последовательности  длиной 503 точки. Для генерирования   

     последовательности использовать функцию randn(). Используя 

     встроенную в  Matlab процедуру  cputime  определить время

     вычисления функции    dftsum(x).

М-файл  для вычисления ДПФ случайной последовательности с помощью функции dftsum(x):

t=0:0.001:0.502;

% Формирование случайной последовательности