Задания для выполнения РГР
по курсу «Теория и обработка сигналов»
Срок сдачи РГР – 16 …17 неделя. Должны быть выполнены 2
задачи из каждого раздела. Номер первой задачи соответствует последней цифре
шифра студента в зачетной книжке, номер второй задачи - последняя цифра плюс 1
(цифре 0 соответствует вариант 10). Оформление РГР – стандартное, для
построения графиков может использоваться Matlab.
1. Раздел 1
1.1. Запишите
в показательной (полярной) форме комплексные числа (выражения)
а) ![]() ,
,
б) ![]() ,
,
в) 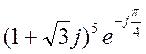
Ответы. а) 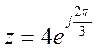 , б)
, б) 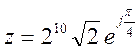 ,
в)
,
в) ![]()
1.2. Пусть сигнал x(t) имеет вид

Найдите x(3t-2).
Ответ.
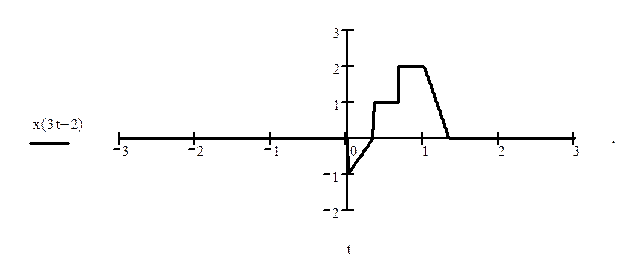
1.3. Дискретный по времени сигнал имеет вид
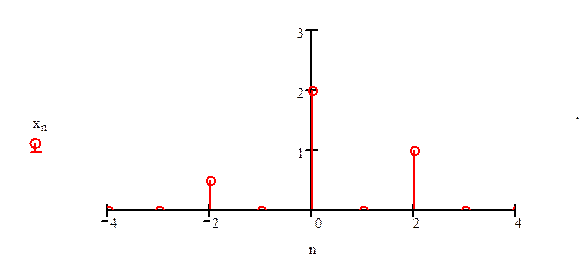
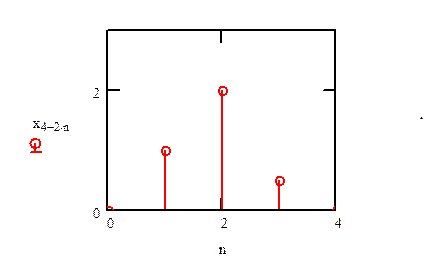
Найдите x[4-2n].
Ответ.
1.4. Определите четную и нечетную составляющие сигнала x(t) и постройте их графики
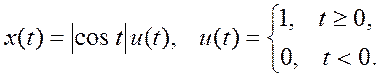
Ответ.
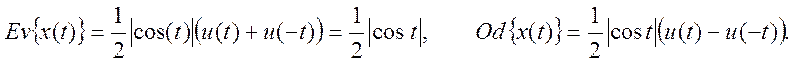
1.5. Пусть
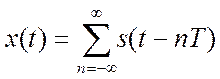
периодический с периодом Т непрерывный во времени сигнал. Изобразите графики сигнала для
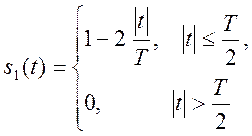
и
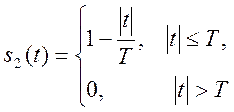
1.6. Найдите период сигнала
![]()
Ответ. Период T = π.
1.7.
Исследуйте характер поведения экспоненциального сигнала дискретного времени ![]() при комплексных значениях
при комплексных значениях ![]() .
.
1.8.
Определите, является ли периодическим сигнал ![]() и
найдите его период.
и
найдите его период.
Ответ.
Периодический сигнал с периодом ![]() .
.
1.9.
Является ли линейной и инвариантной во времени система с уравнением ![]() ?
?
Ответ.
Система – линейная, неинвариантная во времени.
1.10.
Определите, является ли линейной, стационарной (инвариантной во времени) и устойчивой
система- интегратор с уравнением 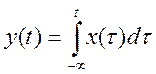 ?
?
Ответ. Система - линейная, инвариантная во времени, но неустойчивая.
2. Раздел 2
2.1. Определите коэффициенты Фурье сигнала и постройте его амплитудный и фазовый спектр
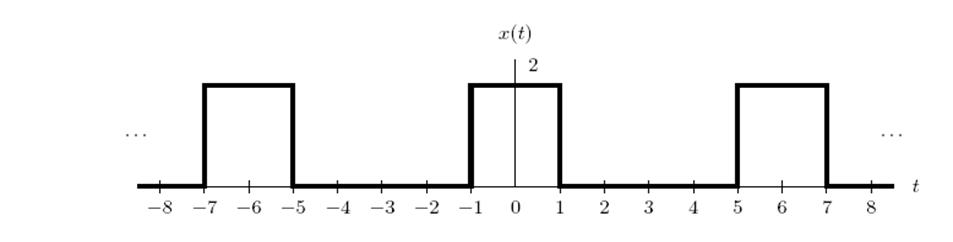
Ответ. 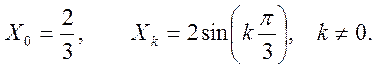
2.1. Найдите коэффициенты комплексной формы ряда Фурье и постройте график амплитудного спектра для сигнала вида квадратной волны


![]()




![]()
![]()
![]()

Ответ: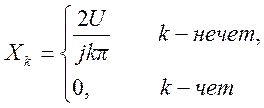
2.2. Найдите коэффициенты Фурье сигнала
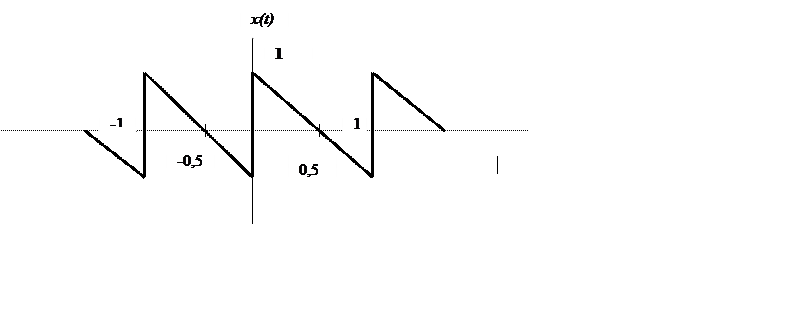 |
Ответ. 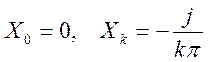
2.3. Определите коэффициенты Фурье сигнала и постройте его амплитудный и фазовый спектр.
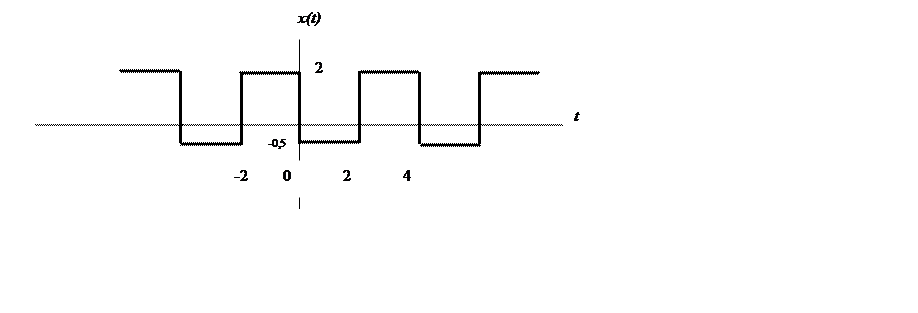
Ответ. 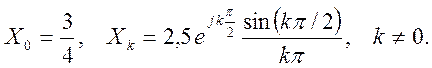 .
.
2.4. Периодическая последовательность импульсов с единичной амплитудой, периодом Т и длительностью 2τ на интервале периода описывается выражением
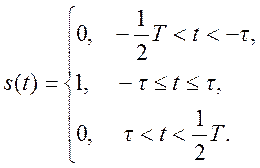
Покажите, что коэффициенты ряда Фурье для такого сигнала имеют вид
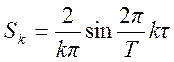 .
Покажите, что при
.
Покажите, что при ![]() коэффициенты не зависят
от k, и спектр состоит из бесконечного числа линий
одинаковой высоты.
коэффициенты не зависят
от k, и спектр состоит из бесконечного числа линий
одинаковой высоты.
2.5.
Определите коэффициенты и ряд Фурье сигнала
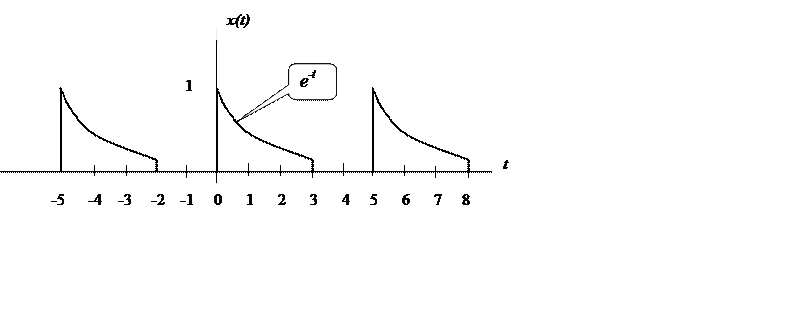 |
Ответ. 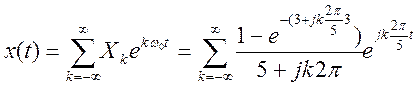
2.7. Определите амплитудный и
фазовый спектры периодического сигнала и постройте их графики
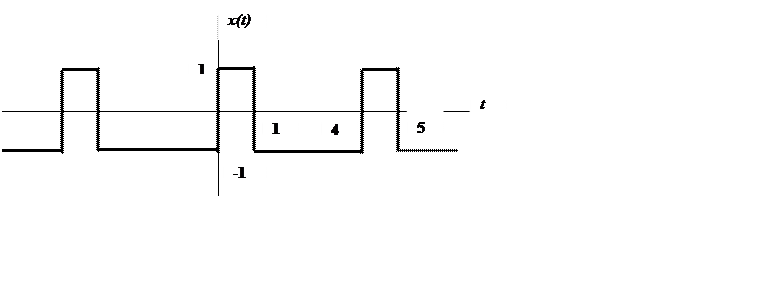
Ответ. 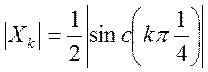 ,
, 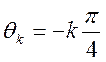
2.8. Разложите в ряд Фурье
сигнал
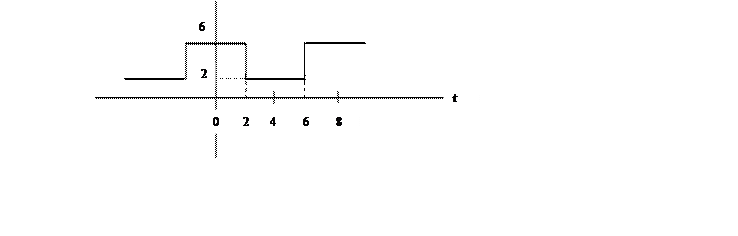
и постройте его амплитудный спектр.
Ответ. 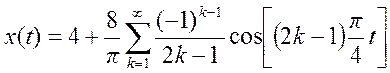
2.9. Определите амплитудный и
фазовый спектры периодического сигнала и постройте их графики

Ответ. 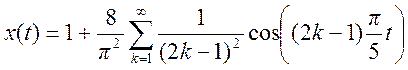
2.10. Определите амплитудный и фазовый спектры периодического сигнала и
постройте их графики
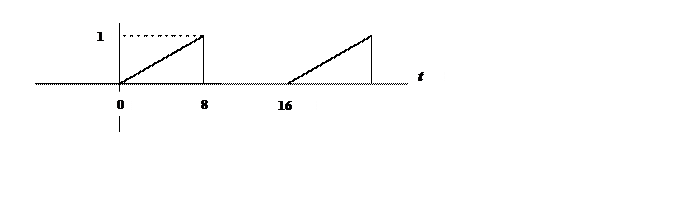
Ответ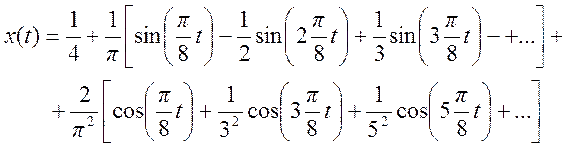
3. Раздел
3
3.1. Определите преобразование Фурье и постройте график амплитудного спектра сигнала
![]() .
.
Ответ: 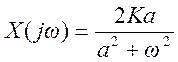
3.2.Вычислите
преобразование Фурье сигнала типа синусоидального импульса
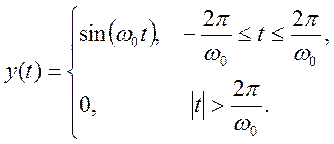
Ответ. 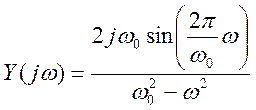
3.3. Найдите спектр Фурье несимметричного треугольного импульса
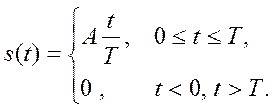
Ответ: 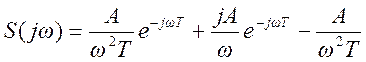
3.4. Используя свойство дуальности преобразования Фурье, определите спектр Фурье комплексного сигнала
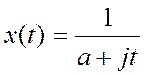
Ответ: ![]()
3.5. Определите преобразование Фурье сигнала непосредственным вычислением и с помощью свойств линейности и временного сдвига

Ответ: ![]()
3.6. Найдите преобразование Фурье и постройте график амплитудного спектра сигнала
![]()
Ответ: 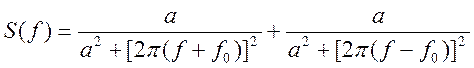
3.7. Дано дифференциальное уравнение, связывающее вход x(t) и выход y(t) системы
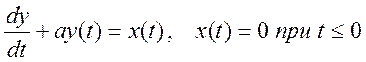 .
.
Найдите преобразование Фурье этого уравнения. Определите отношение
преобразований Фурье левой и правой части, т.е. 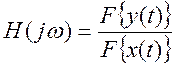 .
Постройте приближенные графики модуля и фазы этого отношения от частоты. Дайте
интерпретацию смысла функций на графиках.
.
Постройте приближенные графики модуля и фазы этого отношения от частоты. Дайте
интерпретацию смысла функций на графиках.
Ответ. 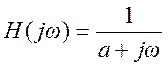 .
.
3.8. Найдите преобразование Фурье и постройте приближенный вид графика амплитудного спектра следующего сигнала
![]() ,
где u(t) - единичная
ступенчатая функция.
,
где u(t) - единичная
ступенчатая функция.
Ответ: 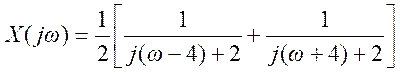 .
.
3.9. Найдите вид сигнала во временной области, если преобразование Фурье сигнала имеет вид
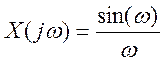 .
.
Ответ. 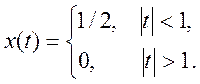
3.10. Постройте
амплитудный спектр сигнала
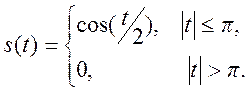
Ответ. 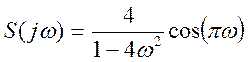
4. Раздел 4.
4.1. Определите ДВПФ сигнала и изобразите график его амплитудного
спектра
а) 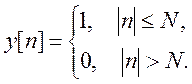
Ответ: 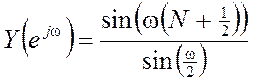 .
.
4.2. . Найдите ДВПФ сигнала
![]() ,
,
Ответ:
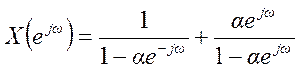 .
.
4.3. Определите ДПФ сигнала ![]() для N=16.
для N=16.
Ответ:
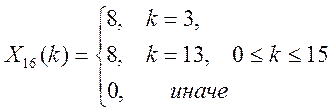
4.4. Определите ДПФ сигнала ![]() .
.
Ответ:
![]()
4.5. Определите и сопоставьте
ДВПФ и ДПФ сигнала ![]() .
.
Ответ:
ДВПФ ![]() ,
,
ДПФ 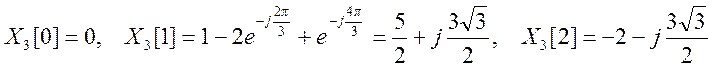
4.6. Докажите, что для
действительной последовательности x[n] амплитудный спектр 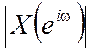 является
четной функцией от ω, а фазовый спектр
является
четной функцией от ω, а фазовый спектр ![]()
- нечетной функцией от ω.
4.7. Найдите вид сигнала x[n], ДВПФ которого
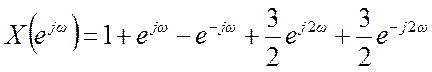 .
.
Ответ. x[-2]=1,5, x[-1]= 1, x[0]=1, x[1]=1, x[2]=1,5.
4.8.
Определите ДПФ сигнала 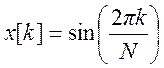 , для N = 8.
, для N = 8.
Ответ: X[k] = {0 2,83-j2,83 0 0 0 0 0 2,83+j2,83}
4.9.
Вычислите ДВПФ и ДПФ сигнала ![]() .
.
Ответ. ![]() ,
, ![]()
4.10. Вычислите ДПФ для сигнала ![]() .
.
Ответ. ![]() .
.
5. Раздел 5.
5.1. Определите
значения свертки двух дискретных сигналов:
![]() и
и ![]() .
Изобразите графики x[n],
h[n] и
.
Изобразите графики x[n],
h[n] и ![]() .
.
Ответ: y = { 3, 8, 14, 8, 3}.
5.2.
Вычислите свертку двух непрерывных сигналов и изобразите её график

Ответ. 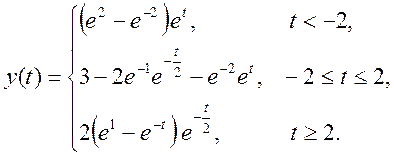
5.3.
Вычислите свертку сигналов
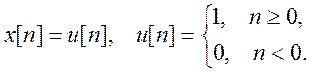
и 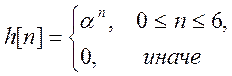 .
.
Изобразите графики x[n], h[n] и ![]() .
.
Ответ. 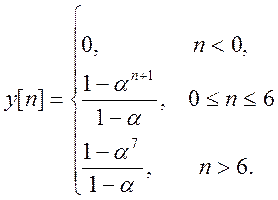
5.4.
Вычислите свертку двух непрерывных сигналов и изобразите её график
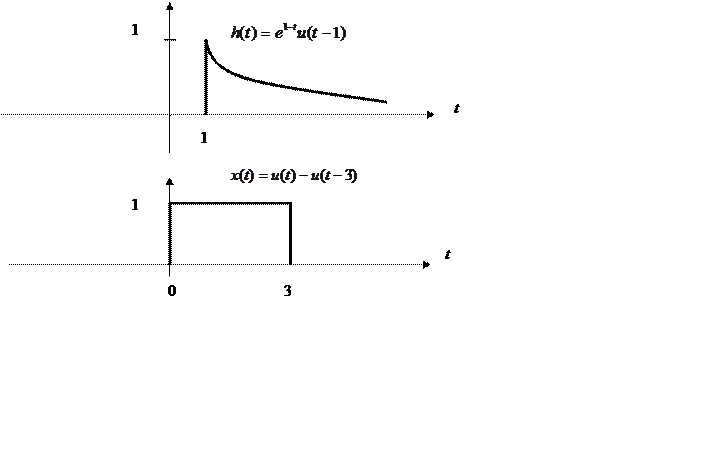 |
Ответ. 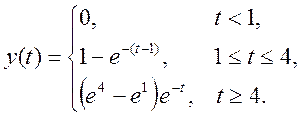
5.5. Вычислите
свертку сигналов
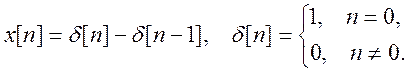
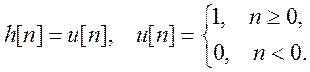
Изобразите графики x[n], h[n] и ![]() .
.
Ответ. ![]()
5.6.
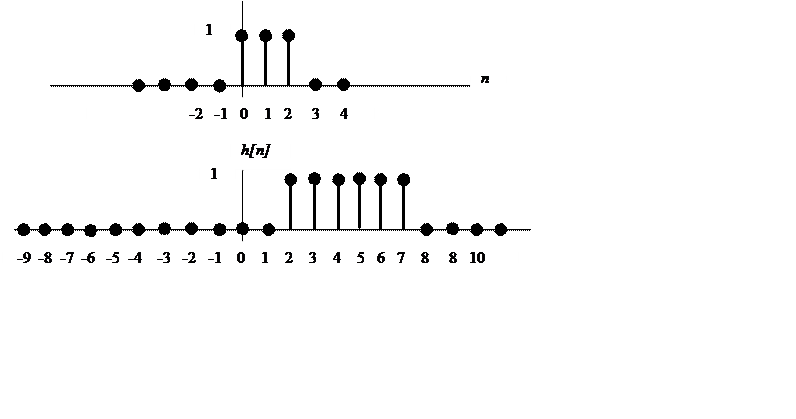 Вычислите свертку сигналов
Вычислите свертку сигналов
Изобразите график свертки.
Ответ. 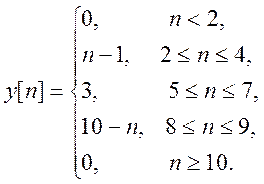
5.7.
Вычислите свертку двух непрерывных сигналов и изобразите её график
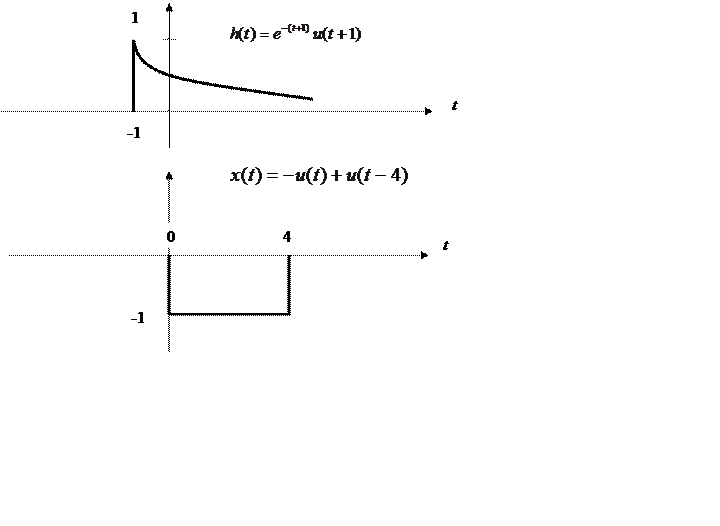 |
Ответ. 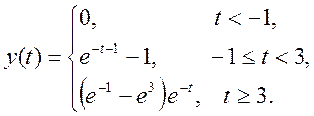
5.8. Вычислите
дискретную свертку двух сигналов, изобразите график свертки
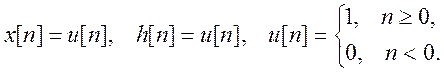
Ответ. ![]()
5.9. Вычислите
свертку двух непрерывных сигналов и изобразите её график
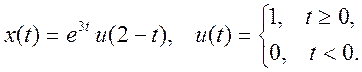
![]() .
.
Ответ. 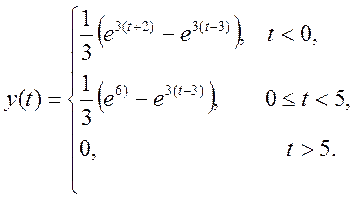
5.10. Вычислите
дискретную свертку сигнала 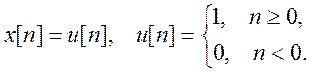
и сигнала 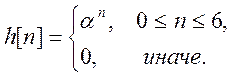
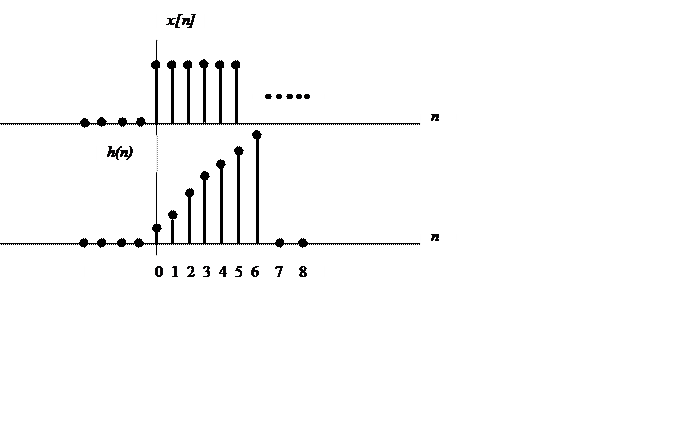
Постройте график свертки.
Ответ. 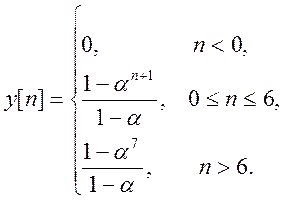
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.