Министерство Образования и Науки РФ
Новосибирский Государственный Технический Университет
Факультет Автоматики и Вычислительной Техники
Кафедра Систем Сбора и Обработки Данных
«Теория и обработка сигналов»
Лабораторная работа № 10
«Линейные дискретные системы»
Вариант 7
Группа: АТ-93 Преподаватель:
Студенты: Кириллова М. доц. Щетинин Ю.И.
Ахмедов А.
Новосибирск - 2012
Цель работы:изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем и приобретение практических навыков их анализа в среде Matlab.
1. Дискретизации аналогового фильтра.
Процедура дискретизации заключается в аппроксимации линейного дифференциального уравнения фильтра разностным уравнением с помощью замены производных конечными разностями и последующих преобразований выражения к виду линейного разностного уравнения с постоянными коэффициентами. При этом интервал между отсчетами сигналов (интервал дискретизации) выбирается на основе теоремы отсчетов. Частота отсчетов должна быть не менее, чем в 2 раза выше верхней граничной частоты спектра обрабатываемого сигнала.
В результате дискретизации получим линейное разностное уравнение и передаточную функцию дискретной системы (фильтра).
Исходные данные: R1=1 кОм, R2=2 кОм, C1=0,5 мкФ
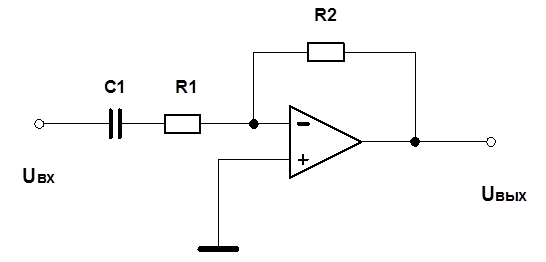
Рис.1 Схема активного фильтра верхних частот
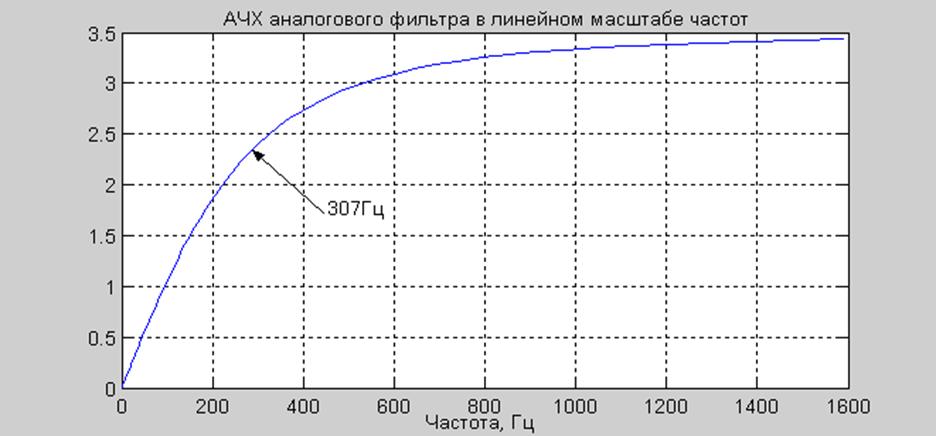
Рис.2 АЧХ аналогового фильтра
Данный фильтр является ФВЧ, т.е.
пропускает высокие частоты лучше, чем низкие. Частота среза –
частота, при которой АЧХ снижается до уровня ![]() (что
соответствует 3 дБ) от максимального значения, fc равна 307 Гц, при выбранных значениях R и C.
(что
соответствует 3 дБ) от максимального значения, fc равна 307 Гц, при выбранных значениях R и C.
Верхняя граничная частота дискретного (цифрового) фильтра равна
половине частоты отсчетов (дискретизации) Fs. Выберем для данного примера значение Fs =10 5 Гц, что соответствует интервалу (периоду) отсчетов
![]()
В предположении идеального операционного усилителя передаточная функция фильтра имеет вид:
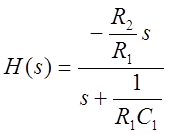 ,
,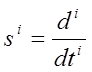 и
и 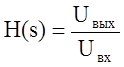
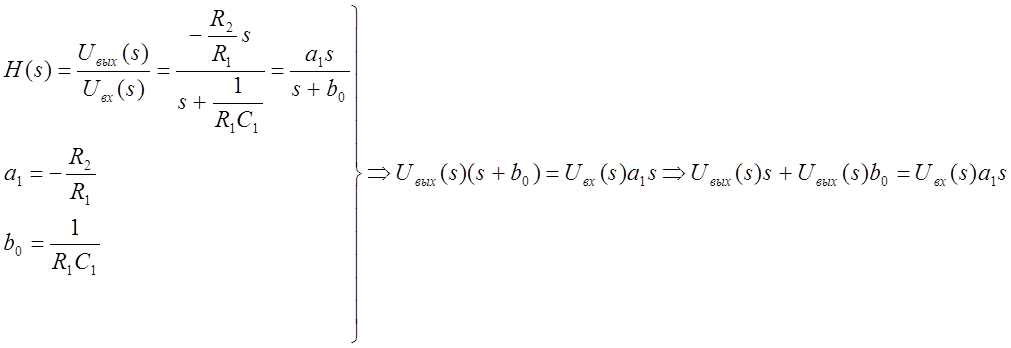 Перейдем к
записи уравнения во временной области, то есть запишем дифференциальное
уравнение, связывающее выходное и входное напряжения фильтра:
Перейдем к
записи уравнения во временной области, то есть запишем дифференциальное
уравнение, связывающее выходное и входное напряжения фильтра:
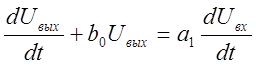 (1)
(1)
Произведем дискретизацию аналогового фильтра с интервалом отсчетов Δt(величина шага приращения времени, интервал дискретизации). Для этого заменим в выражении (1) производную конечной разностью вида:
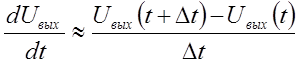
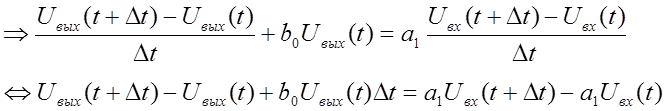 (2)
(2)
Положим ![]() и
и
![]() , и аналогично
, и аналогично
![]() .
.
Тогда выражение (2) примет вид:
![]() . (3)
. (3)
Обозначим ![]() . При этом разностное
уравнение можно представить в виде
. При этом разностное
уравнение можно представить в виде
![]()
![]() (4)
(4)
Для выбранных числовых
значений ![]() значения коэффициентов равны
значения коэффициентов равны ![]() ,
, ![]() и
уравнение (4) перепишем в форме:
и
уравнение (4) перепишем в форме:
![]() (5)
(5)
Возьмем Z- преобразование от левой и правой части уравнения (5). С учетом теоремы сдвига получим:
![]() . (6)
. (6)
Запишем передаточную функцию дискретного фильтра, как отношение Z - преобразований выходного и входного сигналов:
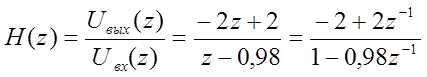 . (7)
. (7)
Нахождение частотной характеристики дискретной системы.
Частотная
характеристика дискретной системы представляет собой передаточную функцию при ![]() , то есть
, то есть
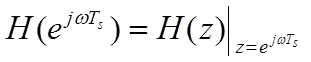 .
.
f = 0:0.01:3000;
%амплитудно-частотная характеристика аналогового фильтра
H1 = 2*j*2*pi*f./(j*2*pi*f+2000);
%период дискретизации
T=0.00001;
% амплитудно-частотная характеристика дискретного фильтра
H2 = (2*exp(j*2*pi*f*T)-2)./(exp(j*2*pi*f*T)-0.99);
figure(1)
plot(f,abs(H1),'r',f,abs(H2),'b')
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
xlabel('f, Гц')
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
legend('АЧХ аналогового фильтра','АЧХ дискретного фильтра')
grid
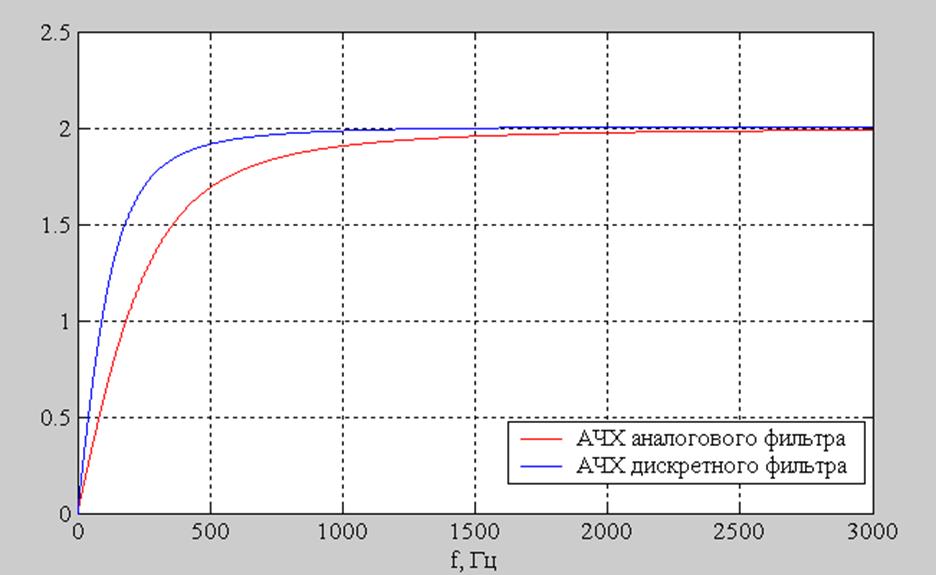
Рис.3. АЧХ аналогового и дискретного фильтров.
АЧХ аналогового и дискретного фильтров соответствуют друг другу, но имеют допустимые расхождения. Следовательно, дискретизация фильтра выполнена верно.
2. Разложение передаточной функции на простые дроби с помощью функции residues(). Получение импульсной характеристики системы.
Воспользуемся следующей последовательностью команд для определения полюсов, вычетов и коэффициентов целой части:
%Вектор коэффициентов числителя:
num=[2 -2];
%Вектор коэффициентов знаменателя:
den=[1 0.98];
[R,P,K]=residuez(num, den)
R =4.0408
P =-0.9800
K =-2.0408
Общий вид результата разложения:
![]() =
= 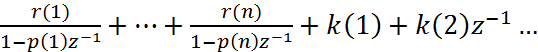
В этой форме представления передаточная функция описывается:
ü вектором – столбцом r вычетов передаточной функции
ü вектором – столбцом p полюсов передаточной функции
ü вектором – строкой k коэффициентов целой части дробно – рациональной функции.
Тогда получим:
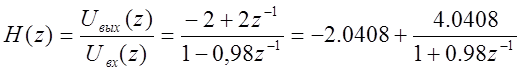 (8)
(8)
Учитывая
что передаточная функция связана
с импульсной характеристикой (импульсную характеристику системы -
обратное Z – преобразование от передаточной функции), ![]() , получим
, получим
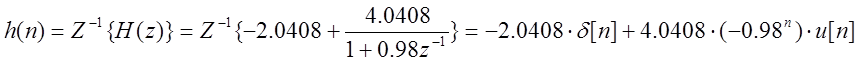
Построим график импульсной характеристики:
Tn=1:1:300;
u_step = 4.0408*power(-0.98,Tn);
u_st = [(4.0408+2.0408) u_step];
Tn = [0 Tn];
stem(Tn,u_st);
Характеристика системы стремится к константе (нулю), значит система устойчива и для ограниченного входного сигнала получим ограниченный выходной сигнал.
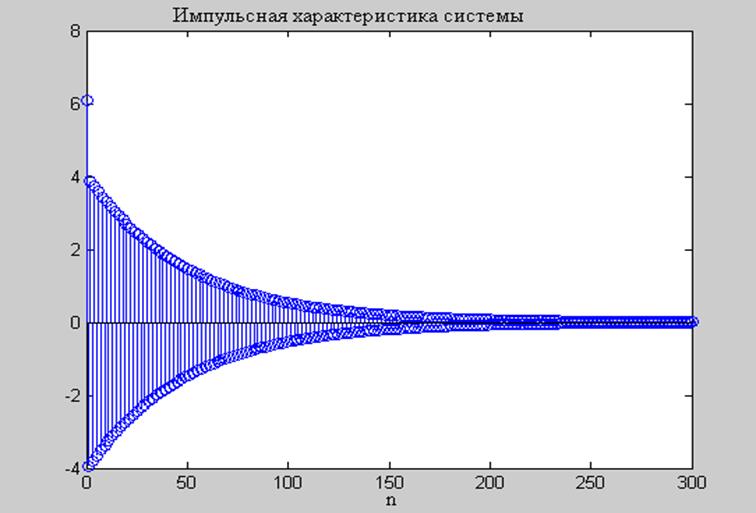
Рис. 4. График аналитически определённой импульсной характеристики.
3. Нахождение нулей и полюсов дискретной системы. Построение диаграммы нулей и полюсов системы с помощью функции zplane.
С помощью следующей программы определим нули и полюса системы и построим диаграмму полюсов и нулей:
%Вектор коэффициентов числителя:
num=[2 -2];
%Вектор коэффициентов знаменателя:
den=[1 -0.98];
nulls = roots(num);
zeros = roots(den);
zplane(num,den)
%--------------------------------------------------------------------------
В результате: nulls =1,
zeros =0.9800
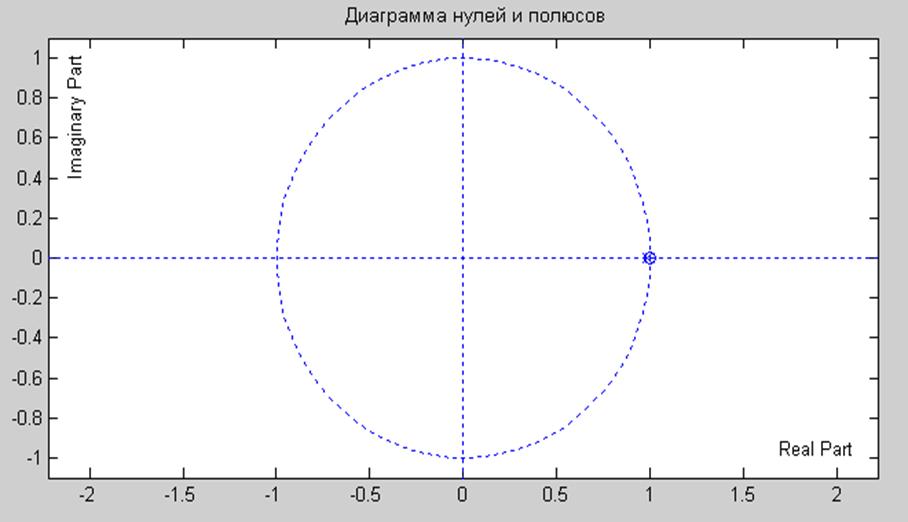
Рис.5 Диаграмма нулей и полюсов системы.
Для отображения нолей и полюсов функции передачи фильтра на комплексной плоскости используется функция zplane(). Поскольку при переходе от преобразования Лапласа к Z – преобразованию левая полуплоскость отображается во внутреннюю часть окружности единичного радиуса, а мнимая ось – в единичную окружность (которая показывается функцией zplane()), то для устойчивости дискретной системы N и D, чтобы полюса её ПФ располагались внутри этой окружности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.