НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
«Z - преобразование
и дискретно – временное преобразование Фурье»
Студентка: Седнев В.С. доц. Щетинин Ю.И.
Цель работы:Изучение Z – преобразования и дискретно – временного преобразования Фурье (ДВПФ), их вычисления в среде Matlab.
1. Нахождение аналитически и
объяснение выражений прямого и обратного Z – преобразования сигналов.
а) x[n] = δ[n],
б) x[n] = u[n],
в) x[n] = cos ωn.
Прямое Z–преобразование:
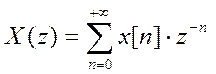
z – комплексная переменная, которая имеет действительную и мнимую часть
![]()
Обратное Z-преобразование:
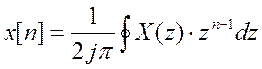
а)x[n] = δ[n]
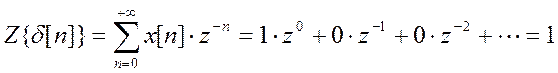
б) x[n] = u[n]
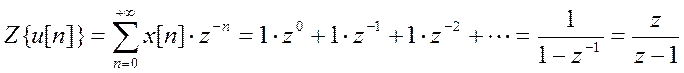
в) x[n] = cos(ω×n)
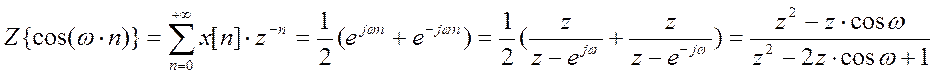
2. Определение Z – преобразования сигналов (последовательностей) в замкнутой форме с помощью функции ztrans() Matlab.
а) x[n] = an cos
ωn,
б) x[n] = n2 e2n,
в) x[n] = cos2 n.
syms w n a
x=a^n.*cos(w*n)
y=(n^2).*exp(2*n)
z=cos(n)^2
f1=ztrans(x) % выполнение Z-преобразований с помощью функции ztrans
f2=ztrans(y)
f3=ztrans(z)
f1, f2, f3
Результаты:
f1 = (z/a-cos(w))*z/a/(z^2/a^2-2*z/a*cos(w)+1)
f2 = z*exp(2)*(z+exp(2))/(z-exp(2))^3
f3 = (z^2+z-3*z*cos(1)^2+cos(1)^2)*z/(z^3+z^2-4*z^2*cos(1)^2-z+4*z*cos(1)^2-1)
3. Определение сигнала во
временной области по его Z – преобразованию с помощью функцию iztrans() Matlab.
а) 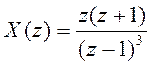 ,
,
б) 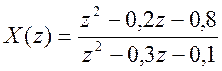 .
.
syms z
x=(z*(z+1))/(z-1)^3
y=(z^2-(0.2*z)-0.8)/(z^2-(0.3*z)-0.1)
f1=iztrans(x) % нахождение сигналов во временной области
f2=iztrans(y) % (нахождение оригиналов) с помощью функции iztrans
f1, f2
Результаты:
f1 = n^2 Т.е. ![]()
f2 = 8*charfcn[0](n)-36/7*(-1/5)^n-13/7*(1/2)^n
charfcn[0](n) в данном случае мы рассматриваем как d-функцию.
Т.е. 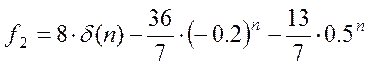
4. С помощью функции residuez() разложите
функцию рационального
Z – преобразования 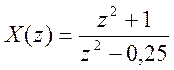 на
простые дроби. Используя
на
простые дроби. Используя
это разложение, найдите аналитически обратное Z – преобразование.
Z- преобразование
имеет вид 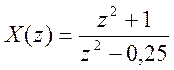
B=[1 0 1]
A=[1 -0,25]
[R,P,K] = RESIDUEZ(B,A)
Результат:
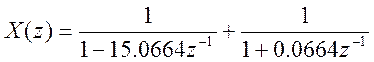 -1
-1
![]()
5. Решите с помощью Z– преобразования линейное разностное уравнение с
постоянными коэффициентами ![]()
Для решения данного уравнения необходимо воспользоваться свойствами линейности и временного сдвига.
Свойство линейности
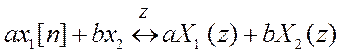
Свойство временного сдвига
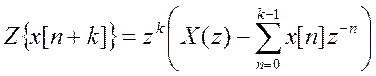
Уравнение
Беря Z-
преобразование от уравнения, с учетом свойства временного сдвига получаем ![]() .
.
Отсюда ![]() .
.
Решение в Z – области
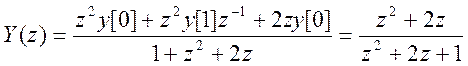
Обратное Z-преобразование
![]() .
.
Поэтому решение уравнения
![]() .
.
6. Запишите и прокомментируйте выражения прямого и обратного ДВПФ. Как
связаны ДВПФ и Z
– преобразование? Аналитически вычислите ДВПФ сигнала
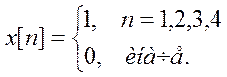
Прямое ДВПФ:
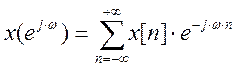
Обратное ДВПФ:
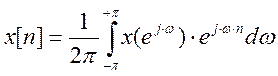
7. Найдите с помощью программы
(DTFT.m) ДВПФ сигналов
а) x[n] = e -0,5n,
б) 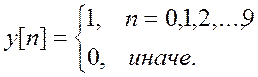
для значения M = 64.
M=64
n=1:9
x(n)=exp(-0.5*n) %исходный сигнал
y(n)=1
[X,w] = DTFT(x,M)
[Y,w] = DTFT(y,M)
figure(1) %
subplot(211) % Построение амплитудного и фазового спектров
plot(w,abs(X)) % экспоненциального сигнала
title('Amplitude spectrum') %
subplot(212) %
plot(w,angle(X)) %
title('Phase spectrum') %
figure(2) %
subplot(211) % Построение амплитудного и фазового спектров
plot(w,abs(Y)) % второго сигнала
title('Amplitude spectrum') %
subplot(212) %
plot(w,angle(Y)) %
title('Phase spectrum') %
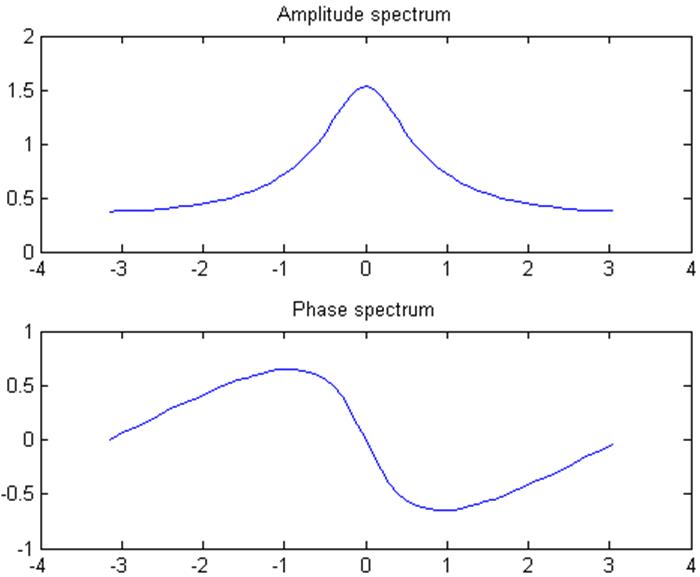
Рис. 1. Амплитудный и фазовый спектры сигнала x[n] = e -0,5n.
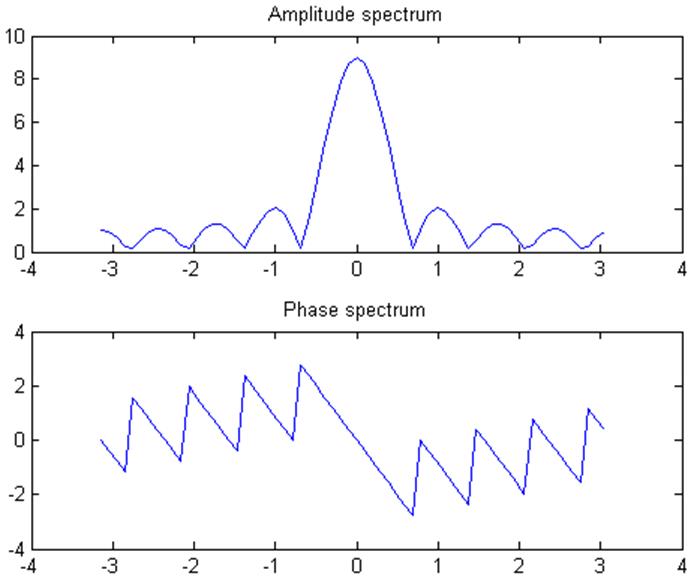
Рис. 2. Амплитудный и фазовый спектры сигнала 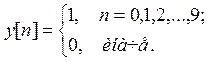
8. Получить частотную характеристику дискретной системы с
уравнением 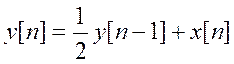 как отношение
как отношение 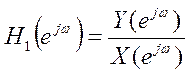 . Найти частотную характеристику инверсной
системы
. Найти частотную характеристику инверсной
системы ![]() . Построить АЧХ, обеих систем с
помощью функции freqz(). Пронаблюдать
особенности работы системы. Построить в одном графическом окне графики прямоугольного
импульса и выходных сигналов каждого фильтра. Объяснить результат:
. Построить АЧХ, обеих систем с
помощью функции freqz(). Пронаблюдать
особенности работы системы. Построить в одном графическом окне графики прямоугольного
импульса и выходных сигналов каждого фильтра. Объяснить результат:
n=20; % интервал частот для построения АЧХ
b=[1]; % числитель частотных характеристик (исходной и инверсной)
a=[1 -0.5]; % знаменатель частотных характеристик (исходной и инверсной)
figure(1);
freqz(b,a,n) % расчет и построение АЧХ исходной системы
figure(2);
freqz(a,b,n) % расчет и построение АЧХ инверсной системы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.