Министерство образования РФ
Новосибирский Государственный Технический Университет
Кафедра ССОД
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 8
Z - преобразование
и дискретно – временное преобразование Фурье
|
Факультет: |
АВТ |
Преподаватель: |
|
Группа: |
АТ-23 |
Щетинин Ю.И. |
|
Студент: |
Переверзина Ю.О. |
|
|
Дата сдачи: |
||
|
Отметка о защите: |
||
Новосибирск
2005
Цель работы:Изучение Z – преобразования и дискретно – временного преобразования Фурье (ДВПФ), их вычисления в среде Matlab.
Прямое и обратное Z-преобразования.
Задание1.
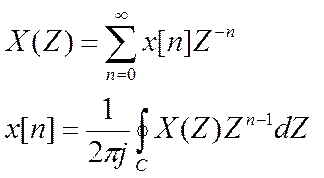
-прямое преобразование Фурье
-обратное преобразование Фурье
Задание2.Z-преобразование сигналов x1[n] = δ[n], x2[n] = u[n], x3[n] = cosω, найденное аналитически.
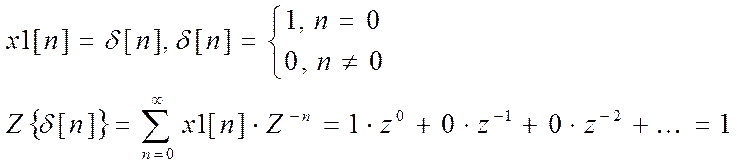
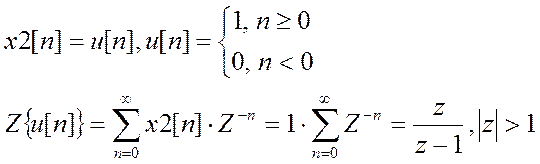
(по формуле суммы геометрической прогрессии)
Z-преобразование
сходится в области ![]() и расходится в области
и расходится в области ![]()
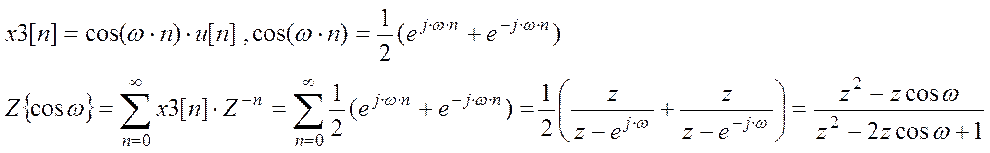
Задание3.Z – преобразования сигналов x1[n] = an cos ωn, x2[n] = n2e2n,
x3[n] = cos2n , вычисленных с помощью функции ztrans().
x1[n] = an cos ωn
>> syms X x a w n ;
>> x=a.^n.*(cos(w.*n));
>> X=ztrans(x);
X=
(z/a-cos(w))*z/a/(z^2/a^2-2*z/a*cos(w)+1) или X=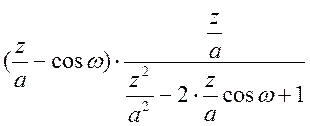
x2[n] = n2 e2
>> syms X n ;
>> x=n.^2.*exp(2.*n);
>> X=ztrans(x);
X=z*exp(2)*(z+exp(2))/(z-exp(2))^3
или X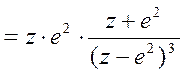
x3[n] = cos2 n
>> syms X n ;
>> x=(cos(n))^2;
>> X=ztrans(x);
X=(z^2+z-3*z*cos(1)^2+cos(1)^2)*z/(z^3+z^2-4*z^2*cos(1)^2-z+4*z*cos(1)^2-1) или
X= 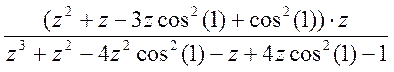
Встроенная функция ztrans()пакета MatLab позволяет во многом ускорить процесс вычисления Z-преобразования. Полученные выражения соответствуют выражениям полученным аналитически:
Оригиналу x1[n] = an cos ωn в таблице соответствует изображение
Z{x1[n]}=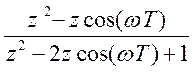 .
.
Оригиналу x1[n]= n2 e2 соответствует изображение
Z{x1[n]}= 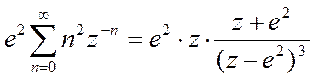 .
.
Задание4.Вычисление сигналов 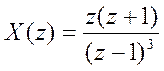 ,
,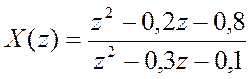 во временной области (оригинал) по их
Z – преобразованиям с использованием функции iztrans().
во временной области (оригинал) по их
Z – преобразованиям с использованием функции iztrans().
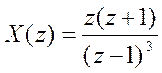
>> syms z x X
>> X=z*(z+1)/(z-1)^3;
>> x=iztrans(X)
x =n^2 или ![]()
Действительно полученный
результат соответствует табличному результату 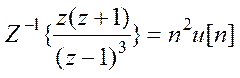
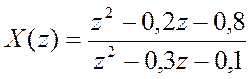
>> syms z x X
>> X=(z^2-0.2*z-0.8)/(z^2-0.3*z-0.1);
>> x=iztrans(X)
x =8*charfcn[0](n)-36/7*(-1/5)^n-13/7*(1/2)^n или
![]()
Задание5. Разложение функции рационального Z – преобразования на простые дроби с помощью функции residuez()и аналитическая проверка результата.
Заданная
функция 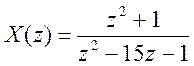
Разложение на простые дроби с помощью встроенной функции MatLab residuez().
>> Num=[1 0 1];
>> Den=[1 -15 -1];
>> [R,P,K] = RESIDUEZ(Num,Den)
R = 1
1
P =
15.0664
-0.0664 K = -1
Учитывая, что R– вектор вычетов, P – вектор полюсов, K – вектор коэффициентов целой части разложения, получаем:
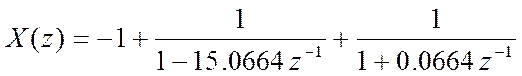
Вычислим обратное Z-преобразование.
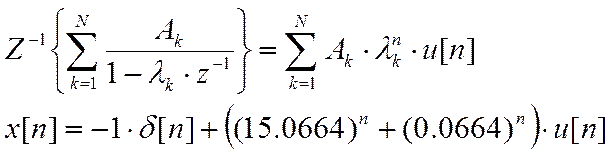
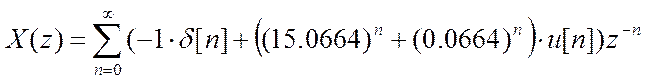
Задание 6.Решение линейного разностного уравнения с постоянными коэффициентами с помощью Z-преобразования.
Уравнение ![]()
Беря Z-
преобразование от уравнения, с учетом свойства временного сдвига и свойства
линейности получаем 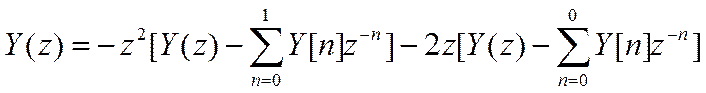
![]()
![]()
![]()
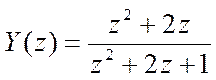
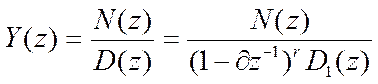
Полюс ![]() имеет
порядок r=2.Разложим Y(z) на простые множители.
имеет
порядок r=2.Разложим Y(z) на простые множители.
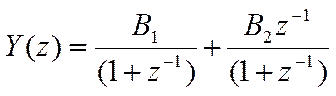 Найдем
Найдем ![]()
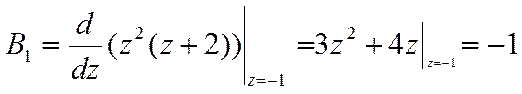
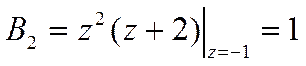
Решение в Z – области
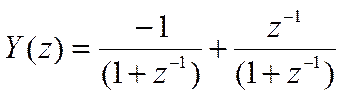
Обратное Z-преобразование и решение уравнения.
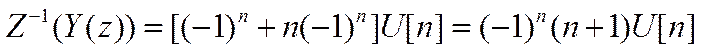
Или 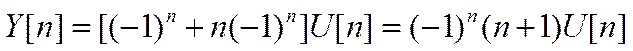
Посчитаем y[0], y[1], y[2]:
Y[0]=1
Y[1]=-2
Y[2]=3
Теперь подставим в исходное уравнение и получим:
![]()
![]()
Задание7. Вычисление ДВПФ сигнала 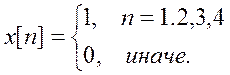
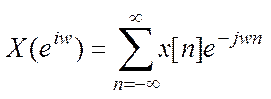 прямое ДВПФ сигнала
прямое ДВПФ сигнала
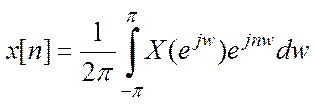 обратное
ДВПФ сигнала
обратное
ДВПФ сигнала
ДВПФ позволяет перейти от дискретной временной функции к непрерывной частотной, при этом частотная функция являеться периодической функцией,поэтому можно сказать, что ДВПФ это ряд Фурье с переменной w.
ДВПФ – это частный случай Z – преобразования (если на единичной окружности ![]() , то Z
– преобразование представляет собой ДВПФ).
, то Z
– преобразование представляет собой ДВПФ).
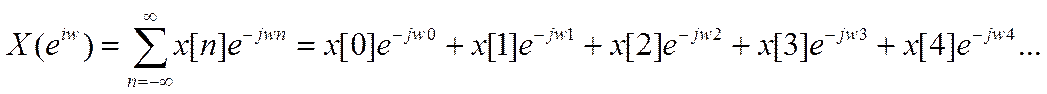
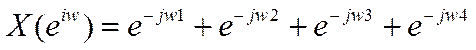
Задание8. Вычисление ДВПФ сигналов x[n]
= e -0,5n,
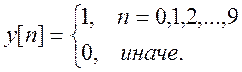
для значения M = 64.
Построение графиков амплитудного и фазового спектров этих сигналов.
n=0:1:62;
x=exp(-0.5.*n);
[X,w]=DTFT(x,64);
n1=-31:1:32;
figure(1); F=8;
N1=64;
plot((n1*F)/N1,abs(X));
figure(2);
plot(angle(X),t);
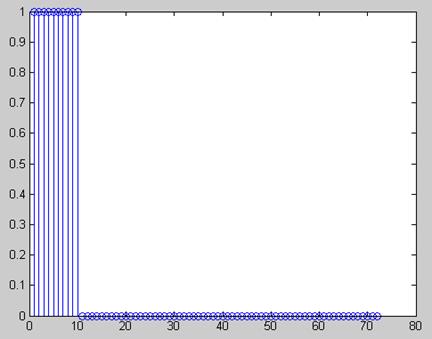
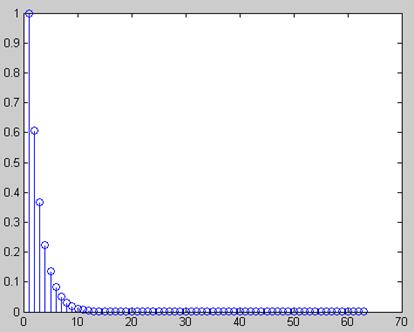
Рис. 1 Сигнал
x[n] = e -0,5n
Рис. 2 Сигнал 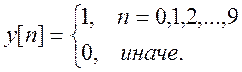
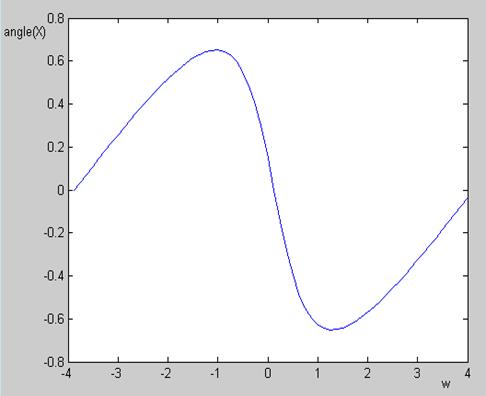
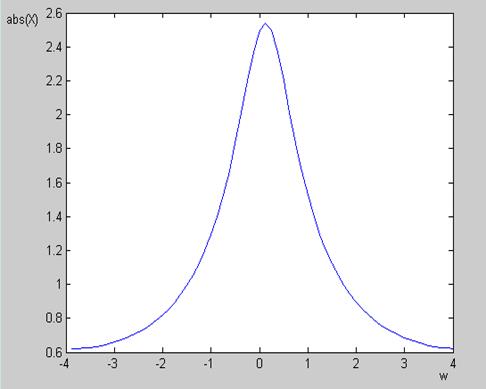
Рис. 3 Амплитудный спектр сигнала x[n] = e -0,5n Рис. 4 Фазовый спектр сигнала x[n] = e -0,5n
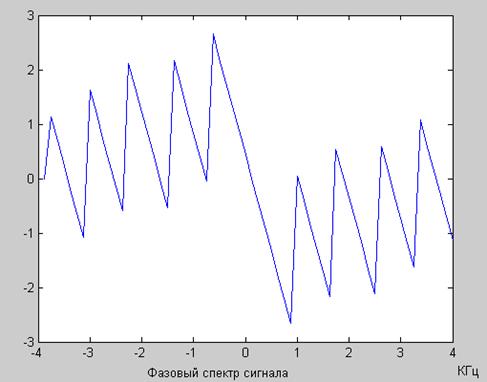
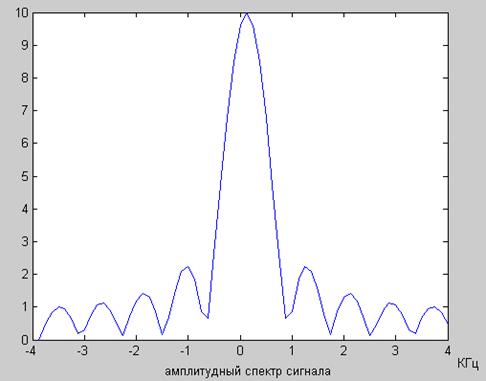
Рис. 5 Амплитудный и фазовый спектры сигнала 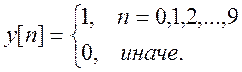
Задание9.Получение частотной характеристики дискретной системы
с уравнением 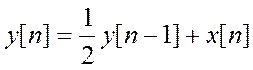 как отношение
как отношение 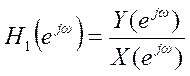 .
.
Нахождение
частотной характеристики инверсной системы ![]() такой,
что последовательное (каскадное) соединение этих систем имеет единичную
частотную характеристику, т.е.
такой,
что последовательное (каскадное) соединение этих систем имеет единичную
частотную характеристику, т.е. ![]() .
.
Построение
АЧХ, т.е. ![]() , обеих систем с помощью функции freqz().
, обеих систем с помощью функции freqz().
Наблюдение особенности работы системы.
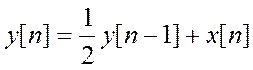
По свойству временного сдвига
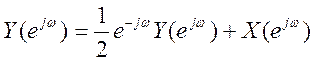
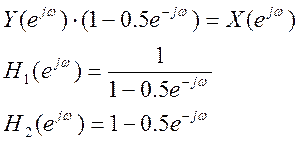
>> num1=[1 0];
>> den1=[1 -0.5];
>> freqz(num1,den1);
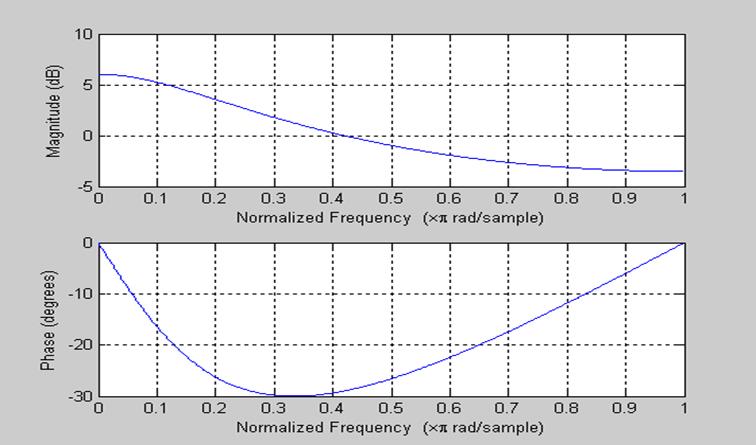
Рис. 4 АЧХ системы H1.
>> num2=[1 -0.5];
>> den2=[1 0];
>> freqz(num2,den2);
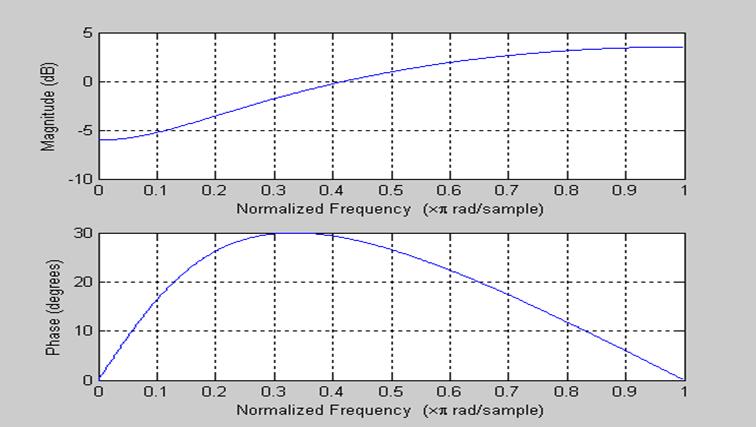
Рис. 5 АЧХ системы H2.
b=[1]; a=[1 -0.5]; n=0:20;
x=rectpuls(n,20);
subplot(3,1,1); stem(n,x);
x1=filter(b, a, x);
subplot (3,1,2); stem (n,x1);
x2=filter(a,b,x1);
subplot (3,1,3); stem (n,x2);
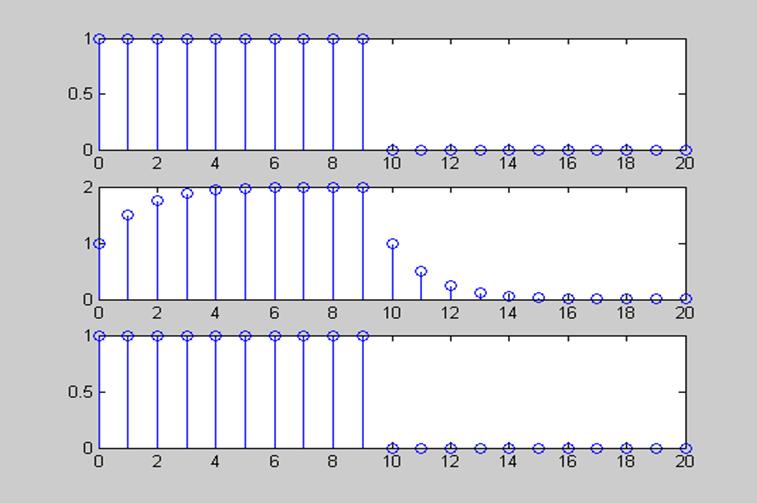
Рис. 6 Графики прямоугольного импульса и выходных сигналов с фильтра H1 и инверсного фильтра H2.
В результате видно, что, пропуская сигнал через инверсный фильтр, получаем исходный сигнал, то есть сигнал полностью восстанавливается.
Задание10. Чтение звукового файла с помощью функции auread(),прослушивание этого файла с помощью функции sound(), добавление шума в звуковой сигнал.
Фильтрация сигнала y1 с помощью функции filter() с параметрами простого цифрового ФНЧ первого порядка из предыдущего пункта.
x1=auread('bird');
sound(x1);
[X,w]=DTFT(x1,0);
y1=x1+randn(length(x1), 1)*0.1;
sound(y1);
[Y,w]=DTFT(y1,0);
y2=filter(1, [1, -0.5], y1);
sound(y2);
[Y2,w]=DTFT(y2,0);
figure(1);
subplot(3,1,1)
X=fftshift(X);
plot(w,abs(X));
subplot(3,1,2)
Y=fftshift(Y);
plot(w,abs(Y));
subplot(3,1,3)
Y2=fftshift(Y2);
plot(w,abs(Y2));
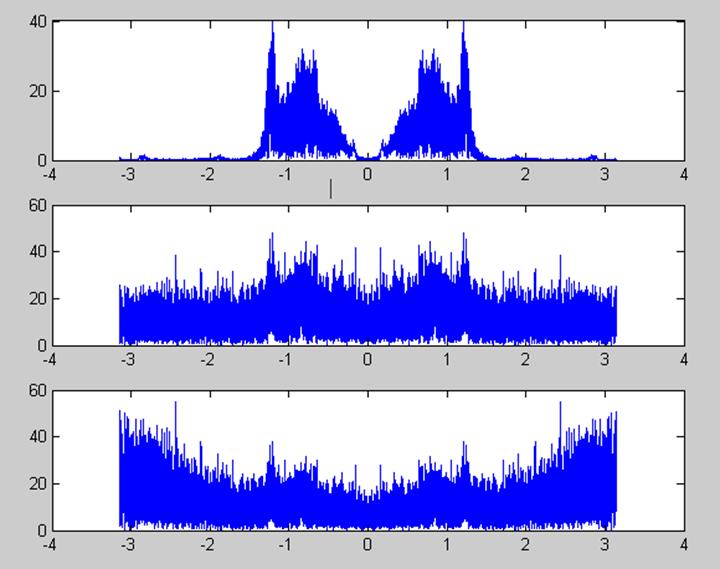
Рис.7 Графики амплитудных спектров исходного сигнала, зашумленного
сигнала и выходного сигнала с фильтра (H1)
Изменив один из коэффициентов фильтра, получим:
y2=filter(1, [1, 0.7], y1);
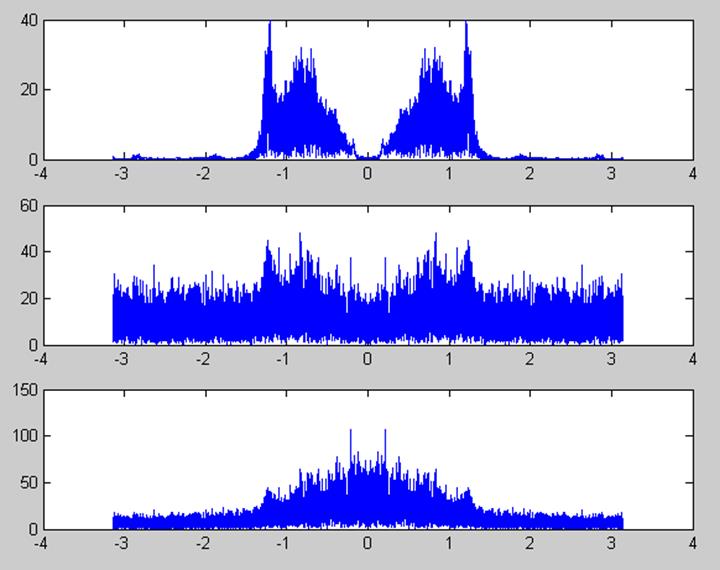
Рис.8 Графики амплитудных спектров исходного сигнала, зашумленного
сигнала и выходного сигнала с фильтра (H1)
При пропускании защумленного сигнала через фильт с параметрами y2=filter(1, [1, -0.5], y1) на выходе получили сигнал большой долей шума и нечетким звучанием.После изменения параметров фильтра y2=filter(1, [1, 0.7], y1) сигнал стал более четким на фоне шума.
В теории и проектировании дискретных систем широко
используется Z – преобразование. Для дискретных систем
оно играет ту же роль, что и преобразование Лапласа для непрерывных систем. Для
последовательности (дискретного сигнала) x[n], n≥0 Z –
преобразование определяется следующим образом 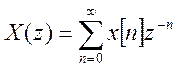 ,
здесь z – комплексная переменная, связанная с
переменной
,
здесь z – комплексная переменная, связанная с
переменной ![]() выражением
выражением ![]() ,
где Td – интервал дискретизации. На
единичной окружности
,
где Td – интервал дискретизации. На
единичной окружности ![]() Z
– преобразование представляет дискретное преобразование Фурье последовательности
(дискретного сигнала) x[n].
Z
– преобразование представляет дискретное преобразование Фурье последовательности
(дискретного сигнала) x[n].
Переход от Z –
преобразования X(z) к
последовательности x[n] во
временной области выполняется с помощью обратного Z – преобразования 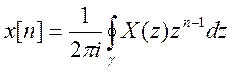 . При этом для
получения временных функций кроме контурного интегрирования применяется также
разложение X(z) на простые
дроби или разложение в степенной ряд
. При этом для
получения временных функций кроме контурного интегрирования применяется также
разложение X(z) на простые
дроби или разложение в степенной ряд
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.