НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра ССОД
ЛАБОРАТОРНАЯ РАБОТА № 4
ДИСКРЕТНОЕ И БЫСТРОЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Группа: АО-61
Студенты: Селиванов Е. Преподаватель:
Щетинин Ю.И.
Новосибирск, 2008г.
Цель работы: Изучение дискретного преобразования Фурье и его свойств, алгоритмов быстрого преобразования Фурье. Приобретение практических навыков вычисления и использования дискретного преобразования Фурье в среде Matlab.
1. Вычисление с помощью функции dftsum() ДПФ следующих сигналов:
а)
![]() для N = 10.
для N = 10.
б) x(n) = 1 для N = 10,
в) x(n) = cos(2πn/10) для N = 10.
Листинг файл-функции dftsum.m:
function X=dftsum(x) % определение функции dftsum(x)
N=length(x); % вычисление количества точек, для исходного сигнала x
for n=0:N-1
for k=0:N-1
R(k+1)=x(k+1).*exp(-2*j*pi.*n.*k./N); % формула для вычисления ДПФ
end
X(n+1)=sum(R);
End
Код MatLab:
% 1) единичного импульса
% 2) единично - ступенчатого импульса
% 3) cos(2*pi*n/10)
% объявление фунций
N=10;
n=0:N-1;
dl=zeros(1,N-1);
dl=[1 dl];
Fdl=dftsum(dl);
one=ones(1,N);
Fone=dftsum(one);
co=cos(2*pi*n/N);
Fco=dftsum(co);
% вывод графиков на экран
figure(1)
subplot(211), stem(n,dl); grid
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('Единичный импульс');
xlabel('N')
subplot(212), stem(n,abs(Fdl)); grid
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('амплитудный спектр')
xlabel('N')
figure(2)
subplot(211), stem(n,one); grid
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('Единично - ступенчатый импульс')
xlabel('N')
subplot(212), stem(n,abs(Fone)); grid
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('амплитудный спектр')
xlabel('N')
figure(3)
subplot(211), stem(n,co); grid
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('cos(2*pi*n/10)')
xlabel('N')
subplot(212), stem(n,abs(Fco)); grid
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('амплитудный спектр')
xlabel('N')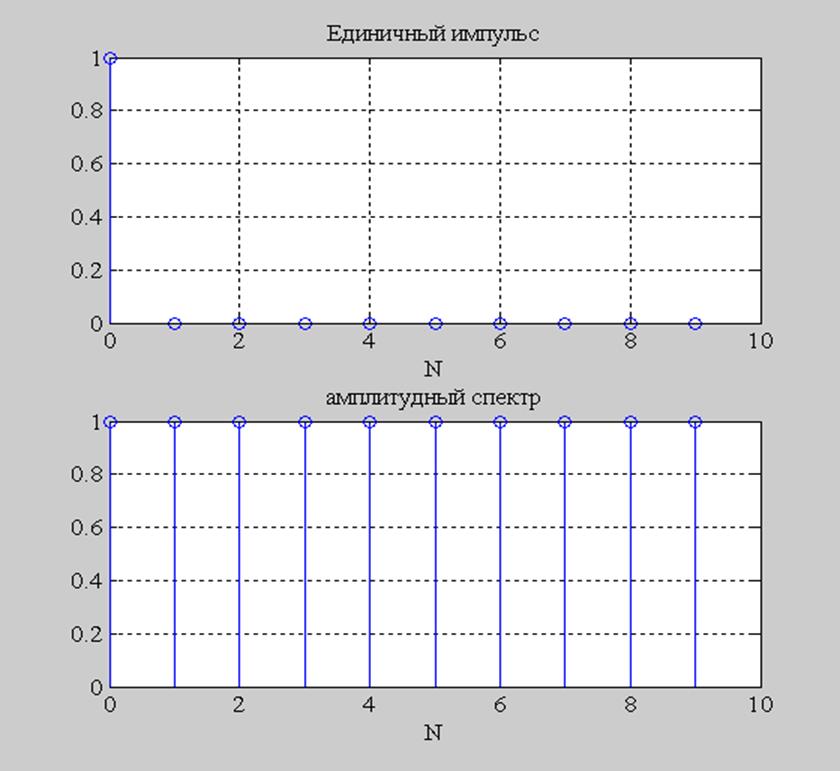
Рис.1. График ![]() и
его амплитудный спектр для N=10
и
его амплитудный спектр для N=10
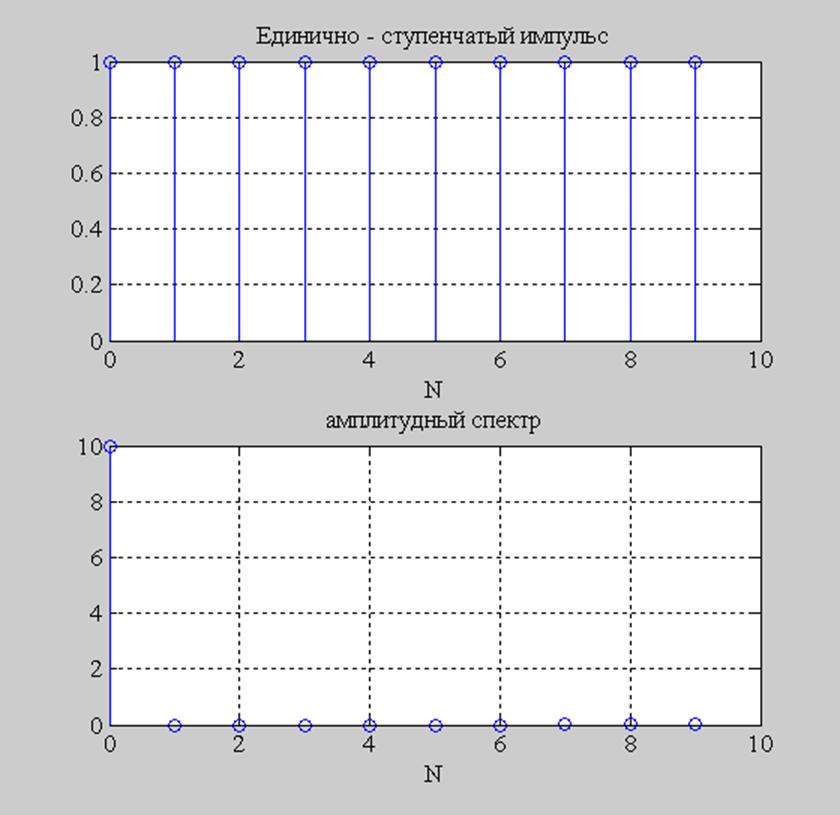
Рис.2. График x(n) = 1 и его амплитудный спектр для N=10
Из рисунков видно, что чем уже сигнал, тем шире его спектр.
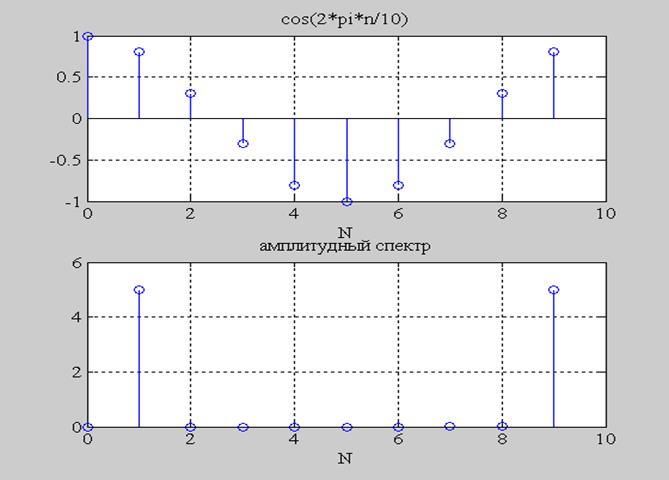
Рис.3. График функции x(n) = cos(2πn/10) и ее амплитудный спектр для N=10.
На рис. 3 возникает дополнительная гармоника на 9 точке отсчета. Она возникает в силу периодичности ДПФ.
2. Написание и использование файл-функции для вычисления ОДПФ.
Листинг файл-функции idftsum.m:
function x=idftsum(X)
% Функция для вычисления дискретного обратного преобразования Фурье (ОДПФ)
N=length(X);
x=zeros(1,N);
for n=1:N,
for k=1:N,
x(n)=x(n)+X(k)*exp(j*2*pi*(n-1)*(k-1)/N)/N;
end
end
x=real(x);
Проверка правильности работы функции idftsum. Сравнение графика сигнала и графика последовательности, полученной путем прямого и обратного преобразования Фурье.
Код MatLab:
N=10;
n=0:N-1;
dl=zeros(1,N-1);
dl=[1 dl];
one=ones(1,N);
co=cos(2*pi*n/N);
figure(1)
subplot(211), stem(n,dl); grid , axis([min(n) max(n) 0 1.5]);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('Единичный импульс')
subplot(212), stem(n,idftsum(dftsum (dl)));
grid, axis([min(n) max(n) 0 1.5]);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('Единичный импульс после прямого и обратного ДПФ')
xlabel('N');
figure(2),
subplot(211), stem(n,one); grid , axis([min(n) max(n) 0 1.5]);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('Единично - ступенчатый импульс')
subplot(212), stem(n,idftsum(dftsum (one)));
grid, axis([min(n) max(n) 0 1.5]);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('Единично - ступенчатый импульс после прямого и обратного ДПФ')
xlabel('N');
figure(3),
subplot(211), stem(n,co); grid, , axis([min(n) max(n) -1.5 1.5]);
title('cos(2*pi*n/10)');
subplot(212), stem(n,idftsum(dftsum (co)));
grid, axis([min(n) max(n) -1.5 1.5]);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('cos(2*pi*n/10) после прямого и обратного ДПФ')
xlabel('N');
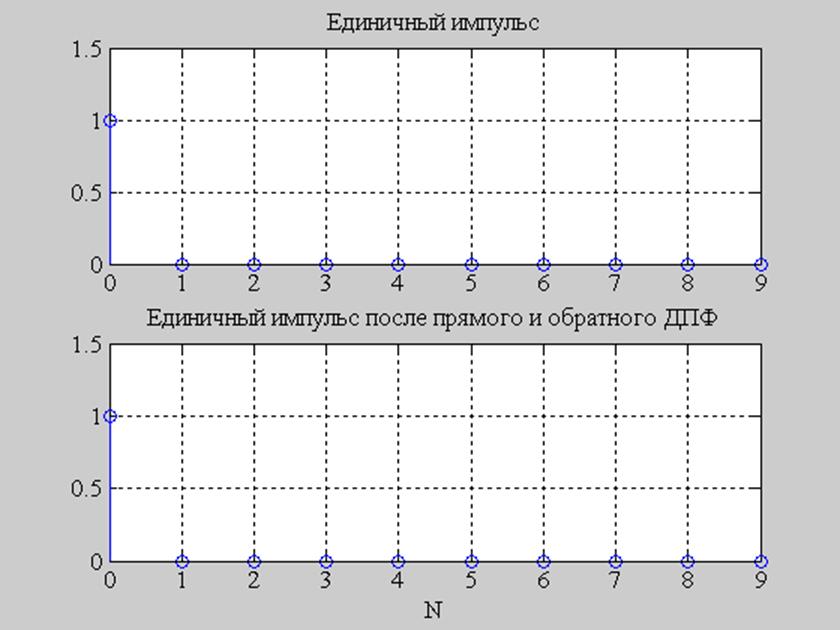
Рис. 4. Исходный сигнал и сигнал после прямого и обратного преобразования Фурье.
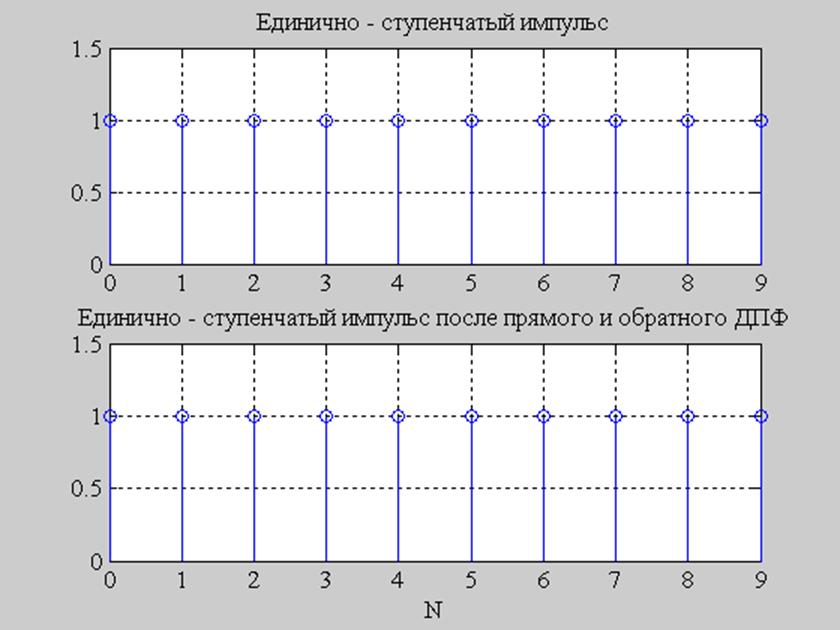
Рис. 5. Исходный сигнал и сигнал после прямого и обратного преобразования Фурье.
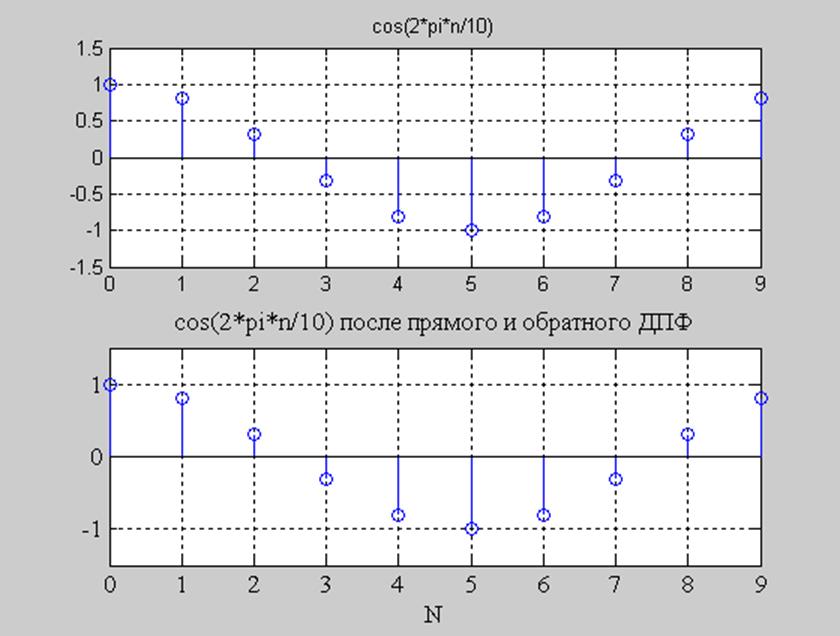
Рис.6. Исходный сигнал и сигнал после прямого и обратного преобразования Фурье.
Выражение idftsum(dftsum( )) выполняет вычисление прямого дискретного преобразования Фурье, с помощью функции dftsum( ), после чего выполняется вычисление обратного преобразования Фурье, с помощью функции idftsum( ). ППФ – переход из временной области в частотную. ОПФ – переход из частотной области во временную.
Из рисунков 4,5,6 видно, что графики исходных сигналов и графики сигналов после прямого и обратного преобразования Фурье совпадают.
При этом сами функции dftsum(), idftsum() имеют одинаковую структуру.
3. Определение времени, за которое вычисляется ДПФ случайной последовательности длиной 1021 точки функцией dftsum(x).
Код MatLab:
dt=0.001;
t=0:dt:0.1020;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=dftsum(x); % Вычисление ДПФ
t2=cputime - t1 % Конец времени вычисления
% Построение графиков во временной и частотной области
Fmax=1/dt; %Вычисляем максимальную частоту
df=1/(dt*length(t)); %Вычисляем частное разрешение
f=0:df:Fmax-dt; %Формируем частотную ось
subplot(211), plot(t,x),grid,
axis([0 0.1020 1.1*min(x) 1.1*max(x)])
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('сигнал'), xlabel('время, сек');
subplot(212), plot(f,dt*abs(y)), grid,
axis([0 (Fmax-dt) 0 abs(1.1*max(dt*y))])
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('Амплитудный спектр'), xlabel('частота, Гц');
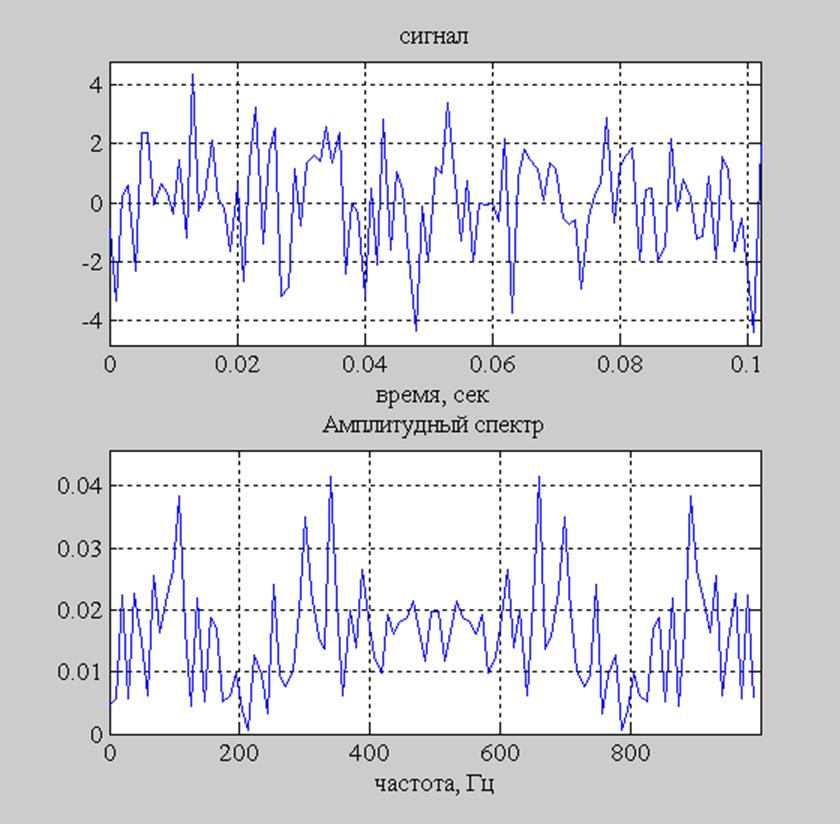
Рис. 7. а) График сигнала сформированного из случайной последовательности;
б) Амплитудный спектр сигнала представленного выше вычисленный функцией dftsum.
Время, за которое было вычислено преобразование Фурье, с помощью функции dftsum, равняется 0.0310 секунды.
4. Определение времени, за которое вычисляется ДПФ случайной последовательности длиной 1021 точки с помощью встроенной в Matlab функции fft().
Код MatLab:
% при помощи функции fft
dt=0.001;
t=0:dt:0.1020;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=fft(x,length(t)); % Вычисление ДПФ
t2=cputime - t1 % Конец времени вычисления
% Построение графиков во временной и частотной области
Fmax=1/dt; % Вычисляем максимальную частоту
df=1/(dt*length(t)); % Вычисляем частное разрешение
f=0:df:Fmax-dt; % Формируем частотную ось
subplot(211), plot(t,x),grid,
axis([0 0.1020 1.1*min(x) 1.1*max(x)])
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('сигнал'), xlabel('время, сек');
subplot(212), plot(f,dt*abs(y)), grid,
axis([0 (Fmax-dt) 0 abs(1.1*max(dt*y))])
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12)
title('Амплитудный спектр'), xlabel('частота, Гц');
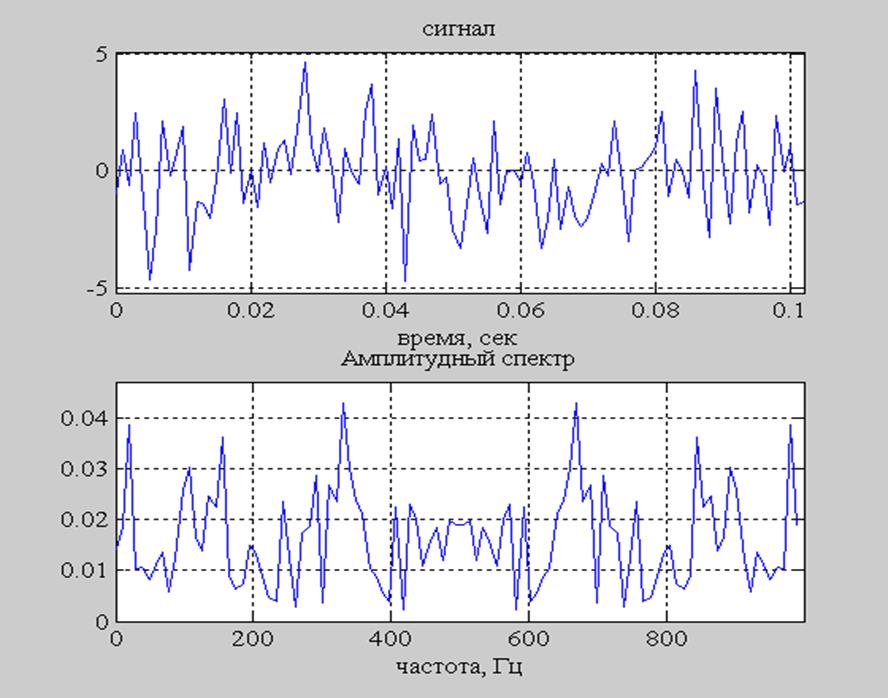
Рис. 8. а) График сигнала - случайной последовательности;
б) Амплитудный спектр сигнала , вычисленный функцией fft.
Время, за которое было вычислено преобразование Фурье, с помощью функции fft 0.0160 сек.
Алгоритм
БПФ, наиболее эффективен, когда размер ДПФ ![]() ,
для того что бы привести размер ДПФ к этому условие последовательность
дополняют нужным числом нулей. Алгоритм заключается, в следующем делим массив
на четные и нечетные последовательности элементов.
,
для того что бы привести размер ДПФ к этому условие последовательность
дополняют нужным числом нулей. Алгоритм заключается, в следующем делим массив
на четные и нечетные последовательности элементов. ![]()
![]() , где
, где ![]() -
БПФ четных членов,
-
БПФ четных членов, ![]() - БПФ нечетных членов. ДПФ
имеет период, равный количеству отсчетов преобразуемой последовательности,
следовательно, вторая половина может быть найдена с учетом этой периодичности.
Итак, ДПФ последовательности x[n] может быть
выражено через ДПФ четной и нечетной последовательностей при всех значениях k.
- БПФ нечетных членов. ДПФ
имеет период, равный количеству отсчетов преобразуемой последовательности,
следовательно, вторая половина может быть найдена с учетом этой периодичности.
Итак, ДПФ последовательности x[n] может быть
выражено через ДПФ четной и нечетной последовательностей при всех значениях k.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.