Министерство науки и образования РФ
Новосибирский государственный технический университет
Лабораторная работа № 11
по дисциплине "Теория и обработка сигналов"
Цифровые фильтры с конечной импульсной характеристикой
Выполнил: Преподаватель: к.т.н., доцент
Студент: Макаров С.В. Щетинин Ю.И.
Группа: АИ-92
Факультет: АВТ
Новосибирск
2012
Цель работы: изучение методов анализа и синтеза фильтров с конечной импульсной характеристикой (КИХ – фильтры, другое название – нерекурсивные фильтры) с использованием сглаживающих оконных функций.
1. Построение импульсной характеристики КИХ - фильтра нижних частот с прямоугольным окном
Импульсная характеристика идеального фильтра
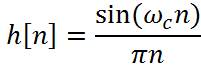
Идеальный ФНЧ не может быть физически реализован, поэтому его импульсную характеристику ограничивают конечной длиной N. Такую импульсную характеристику можно определить по выражению [1, 2]:
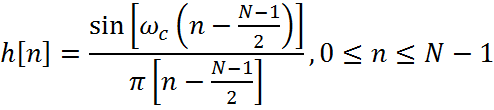
С помощью следующего кода MATLAB
построим импульсные характеристики КИХ-фильтра нижних частот с прямоугольным
окном, нормированной частотой среза ![]() для двух значений длины фильтра N = 14 и N = 50.
для двух значений длины фильтра N = 14 и N = 50.
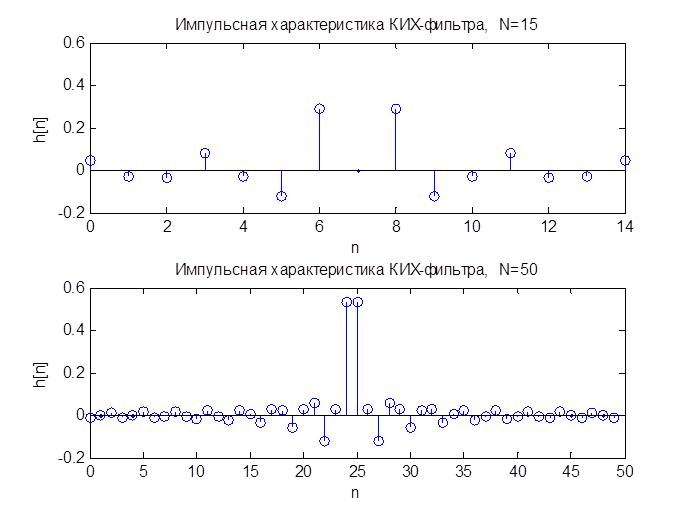
Рис.1 Импульсные характеристики КИХ-фильтров
2. Построение графиков АЧХ КИХ-фильтра
N1 = 14, N2 = 50, n1 = 0:N1-1, n2 = 0:N2-1, wc = 2;
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
[H1,w] = DTFT(h1,512);
[H2,w] = DTFT(h2,512);
%Графики АЧХ в линейном масштабе
figure (1);
subplot(211);
plot(w,abs(H1)./max(abs(H1))), grid;
title('АЧХ в линейном масштабе при N = 14');
ylabel('|H1|/max(|H1|)');
subplot(212);
plot(w,abs(H2)./max(abs(H2))), grid;
title('АЧХ в линейном масштабе при N = 50');
xlabel('w'), ylabel('|H2|/max(|H2|)');
%Графики АЧХ в логарифмическом масштабе
figure (2);
subplot(211);
plot(w,20*log10(abs(H1)));
title('АЧХ в логарифмическом масштабе при N = 14');
ylabel('20lg(|H1|)');
subplot(212);
plot(w,20*log10(abs(H2)));
title('АЧХ в логарифмическом масштабе при N = 50');
xlabel('w'), ylabel('20lg(|H2|)');
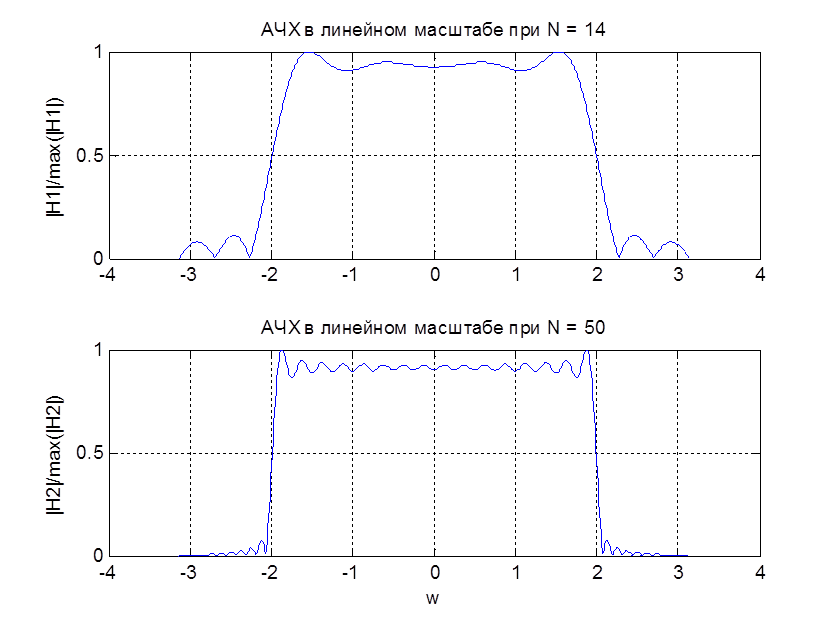
Рис. 2. АЧХ в линейном масштабе
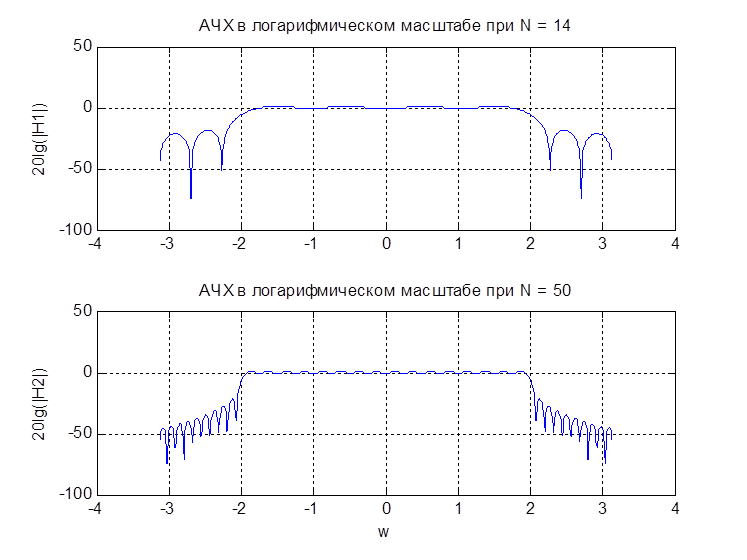
Рис. 3. АЧХ в логарифмическом масштабе
По рис. 2 и рис. 3 видим, что у реального фильтра, по сравнению с идеальным ФНЧ появилась переходная область и наблюдаются пульсации в полосе пропускания и полосе задерживания.
Определим полосу пропускания, задерживания и переходную область АЧХ используя график в линейном масштабе:
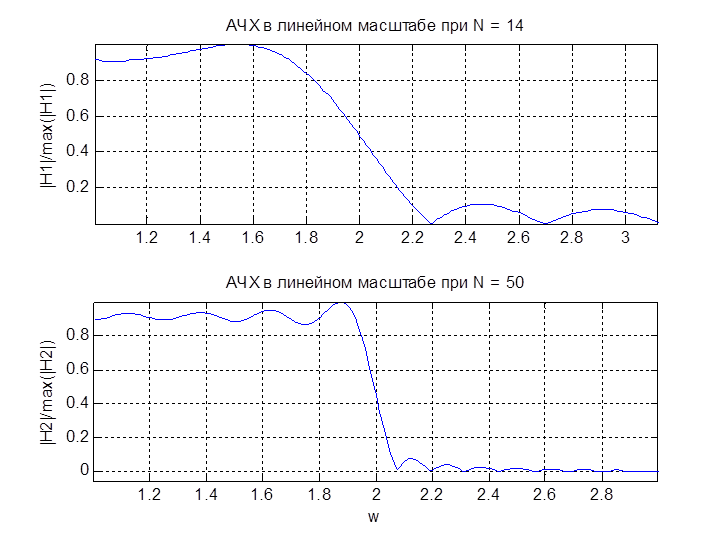
Рис. 4. Увеличенные фрагменты АЧХ в линейном масштабе
|
N |
Полоса пропускания, Гц |
Переходная область, Гц |
Полоса задерживания, Гц |
|
14 |
0 - 1.88 |
1.88 - 2.27 |
> 2.27 |
|
50 |
0 - 1.96 |
1.96 - 2.07 |
> 2.07 |
Из таблицы видим, что при увеличении N фильтра, происходит сужение переходной области АЧХ фильтра. По рис. 2 - 4 видно, что после усечения ИХ фильтра наблюдаются пульсации в полосе пропускания и полосе задерживания. Амплитуда данных пульсаций при увеличении порядка фильтра практически не изменятся, но количество их возрастает. Эти пульсации объясняются эффектом Гиббса.
3. Фильтрация сигнала с помощью двух фильтров
С помощью следующего кода MATLAB отфильтруем сигнал при помощи каждого из фильтров и, проанализировав АЧХ сигналов и прослушав сигналы, сделаем вывод:
load('speech.mat');
N1 = 14, N2 = 50, n1 = 0:N1-1, n2 = 0:N2-1, wc = 2;
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2));
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2));
% фильтрация сигнала
y1 = conv(nspeech2, h1);
y2 = conv(nspeech2, h2);
% спектр исходного сигнала
[Y,w] = DTFT(nspeech2, 512);
subplot(3,1,1);
plot(w,abs(Y));
title ('Амплитудный спектр исходного сигнала');
% спектр сигнала после фильтрации (N = 15)
[Y1,w] = DTFT(y1,512);
subplot(3,1,2);
plot(w,abs(Y1));
title ('Амплитудный спектр после фильтрации (N = 15)');
% спектр сигнала после фильтрации (N = 50)
[Y2,w] = DTFT(y2,512);
subplot(3,1,3);
plot(w,abs(Y2));
title ('Амплитудный спектр после фильтрации (N = 50)');
xlabel('w');
sound(nspeech2) % исходный сигнал
sound(y1) % отфильтрованный сигнал при N = 15
sound(y2) % отфильтрованный сигнал при N = 50
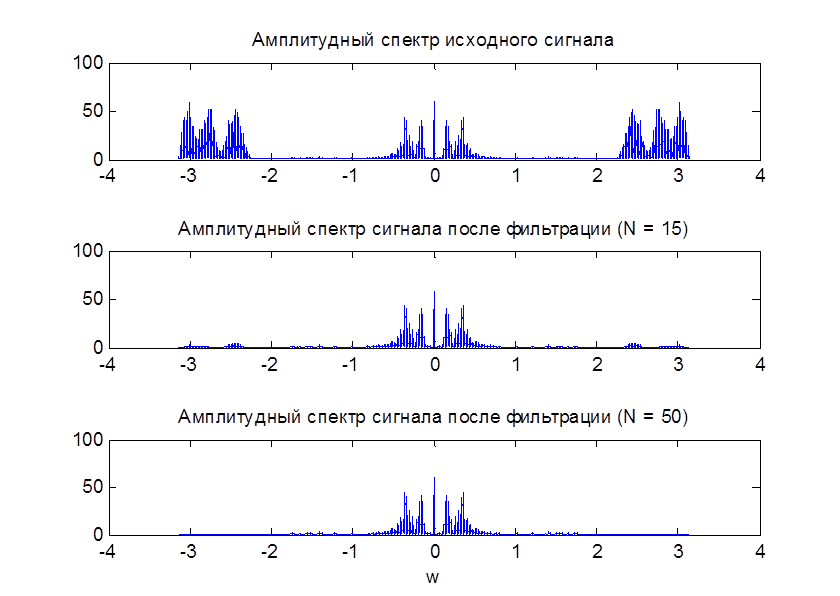
Рис. 5. АЧХ исходного сигнала и отфильтрованных сигналов
Исходный сигнал представляет собой смесь полезного сигнала (речь) с фоновым шумом. Частота звучания речи ниже частоты звучания шума (видно на рис. 5), поэтому мы можем отфильтровать полезный сигнал от шума с помощью фильтров нижних частот.
При фильтрации исходного сигнала
фильтром с N=14 высокочастотные составляющие
подавляются и шумы при прослушивании уменьшаются (на графике 2 рис. 5 можно
наблюдать, что составляющие с частотами выше ![]() ослаблены).
ослаблены).
При фильтрации исходного сигнала
фильтром с N=50 высокочастотные составляющие подавляются полностью и при
прослушивании шумы не различимы, зато четко слышится полезный сигнал - речь
(записана фраза "If you can hear this clearly you filter the signal
correctly"). На графике 3 рис. 5 видно, что составляющие с частотами выше ![]() отсутствуют.
отсутствуют.
4. Построение графиков прямоугольного окна, окон Хэмминга, Ханна и Блэкмана
С помощью следующего кода MATLAB построим графики окон для N=25, используя команды hamming, hann, blackman
N = 25; n = 0:N-1;
h1 = rectpuls(n-12,N-2);
h2 = hamming(N);
h3 = hann(N);
h4 = blackman(N);
plot(n,h1,n,h2,n,h3,n,h4);
title('Графики оконных функций');
legend('Прямугольное окно','Окно Хэмминга','Окно Ханна','Окно Блэкмана');
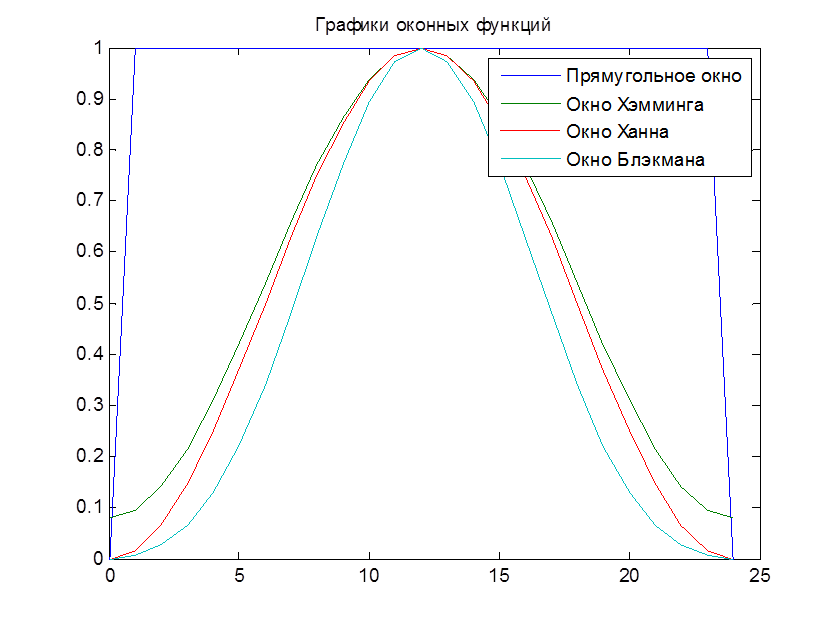
Рис. 6. Графики окон
5. Вычисление ДВПФ оконных функций и построение их спектров
C помощью следующего кода MATLAB построим графики амплитудных спектров прямоугольного окна и окон Хэмминга, Ханна, Блэкмана.
N=25;
h1 = rectpuls(n-12,N-2);
h2 = hamming(N);
h3 = hann(N);
h4 = blackman(N);
[H1,w]=DTFT(h1,512);
[H2,w]=DTFT(h2,512);
[H3,w]=DTFT(h3,512);
[H4,w]=DTFT(h4,512);
subplot(411)
plot(w,20*log10(abs(H1))), axis([-4, 4, -50, 50]),grid
title ('Прямоугольное окно')
subplot(412)
plot(w,20*log10(abs(H2))), axis([-4, 4, -50, 50]),grid
title ('Окно Хэмминга')
subplot(413)
plot(w,20*log10(abs(H3))), axis([-4, 4, -50, 50]),grid
title ('Окно Ханна')
subplot(414)
plot(w,20*log10(abs(H4))), axis([-4, 4, -50, 50]),grid
title ('Окно Блэкмана')
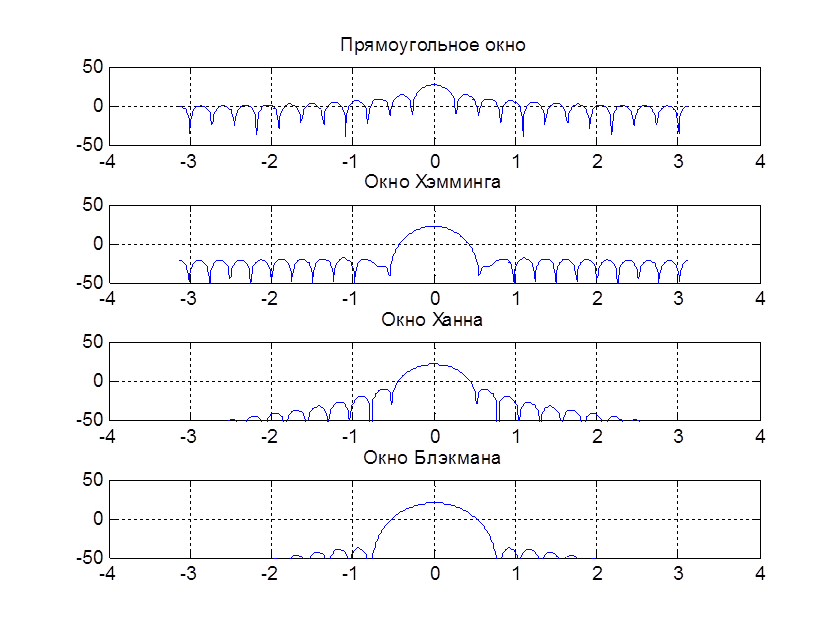
Рис. 7. АЧХ окон в логарифмическом масштабе
На рис. 7 видно, что графики амплитудных спектров имеют пульсации. Часть спектра между двумя первыми нулями - главный лепесток. Чем шире главный лепесток, тем шире переходная полоса фильтра. Другие пульсации - боковые лепестки. Амплитуды боковых лепестков влияют на величину пульсаций амплитудного спектра в полосе пропускания и полосе задерживания.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.