Изучение методов анализа и синтеза фильтров с конечной импульсной характеристикой, страница 2

6. Определение ширины главного лепестка и относительного уровня боковых лепестков амплитудных спектров окон

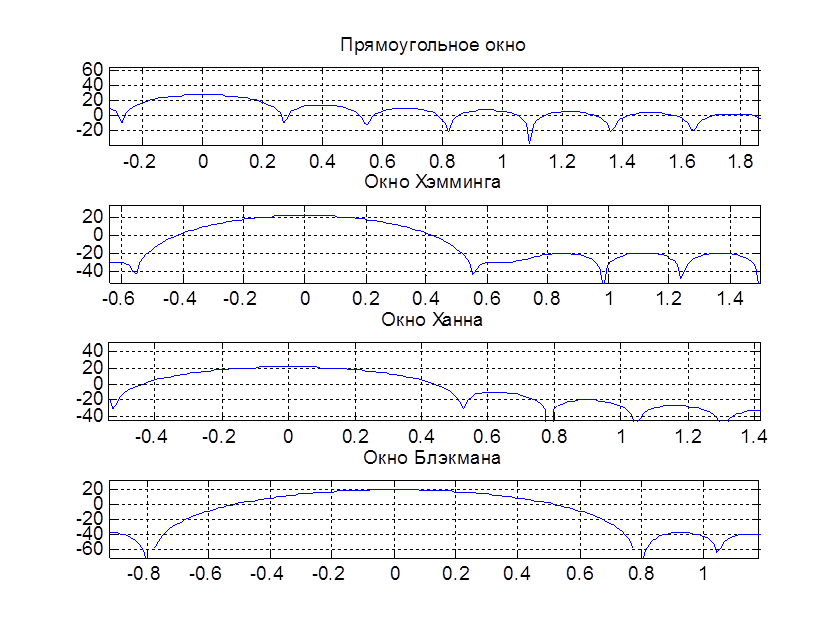
Рис. 7. Масштабированные АЧХ окон в логарифмическом масштабе

Тип окна	Ширина главного лепестка			Относительный  уровень боковых лепестков, дБ
	Теоретическое	Измеренное	Разность	Теоретический	Измеренный	Разность
Прямоугольное	0.5026	0.54	0.0374	-13	-13.23	0.23
Ханна	1.005	1.055	0.05	-31.5	-31.6	0.1
Хэмминга	1.005	1.104	0.099	-42	-41.3	0.7
Блэкмана	1.507	1.5952	0.0882	-58	58	0

7. Построение графиков окна Кайзера и его АЧХ для N=25 и разных β

С помощью следующего кода MATLAB выполним построение графиков окна Кайзера и АЧХ этих окон для N=25, β=0, 1, 5.

N=25;

k1=kaiser(N,0);

figure(1), subplot(211), stem(k1)

title ('Окно Кайзера при  \beta= 0')

[K1,w]=DTFT(k1,512);

subplot(212), plot(w,abs(K1))

title ('Амплитудный спектр'), xlabel('w');

k2=kaiser(N,1);

figure(2), subplot(211), stem(k2)

title ('Окно Кайзера при \beta = 1')

[K2,w]=DTFT(k2,512);

subplot(212), plot(w,abs(K2))

title ('Амплитудный спектр'), xlabel('w');

k3=kaiser(N,5);

figure(3), subplot(211), stem(k3)

title ('Окно Кайзера при \beta = 5')

[K3,w]=DTFT(k3,512);

subplot(212), plot(w,abs(K3))

title ('Амплитудный спектр'), xlabel('w');

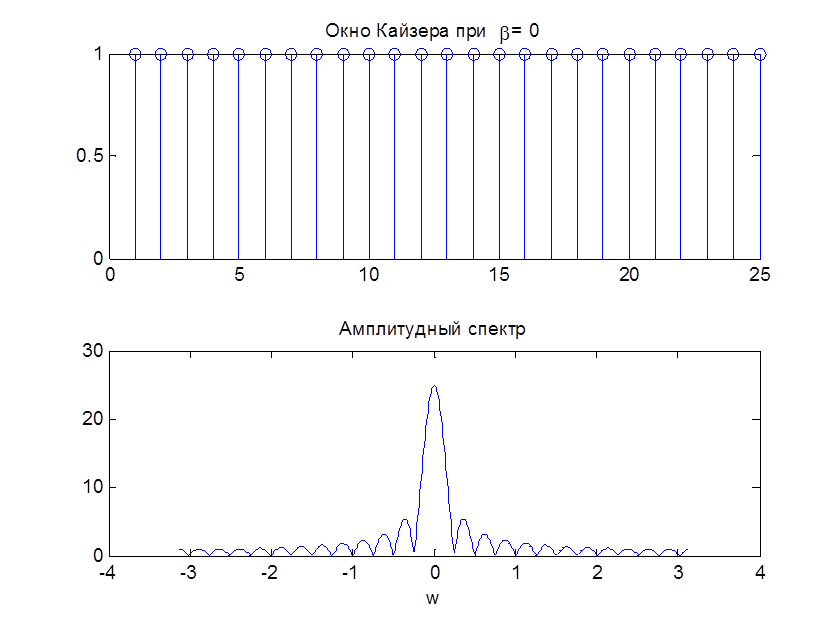
Рис. 8. Окно Кайзера и его АЧХ при N=25, β=0

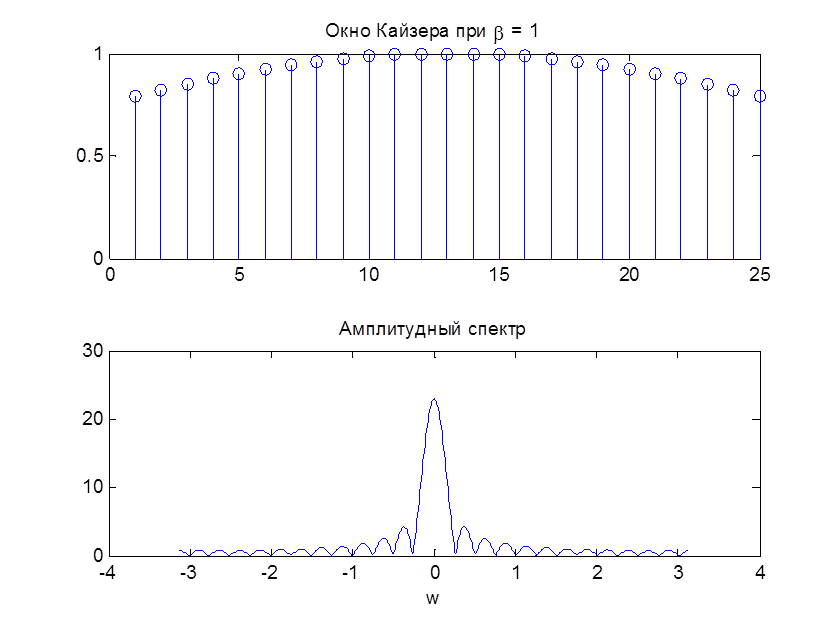
Рис. 9. Окно Кайзера и его АЧХ при N=25, β=1

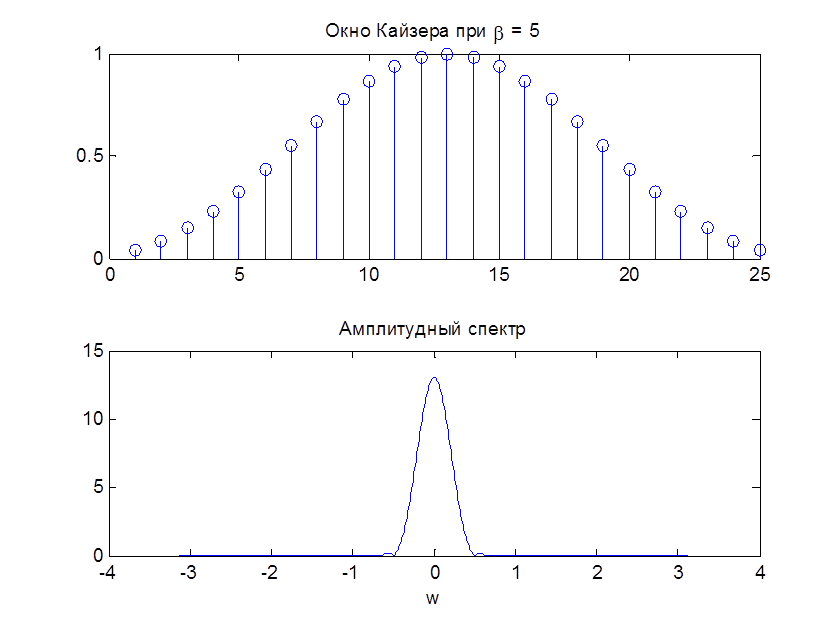
Рис. 10. Окно Кайзера и его АЧХ при N=25, β=5

Параметр β	Ширина главного лепестка	Относительный  уровень боковых лепестков, дБ
0	0.5	19.55
1	0.52	18.85
5	1	12.9

При увеличении параметра β окно спадает к нулю более плавно. Чем больше бета, тем большая энергия приходится на главный лепесток (главный лепесток шире) и тем меньше уровень боковых лепестков.

Из этого следует, что уменьшаются пульсации в полосе задерживания фильтра, но одновременно с этим увеличивается ширина переходной полосы (главный лепесток становится шире)

8. Синтез фильтра по заданным условиям

0.5π	0.6π	0.005	0.006

Произведем расчет фильтра, удовлетворяющего данным условиям:

1.  Нормированные граничные частоты полосы пропускания и полосы задерживания составляют 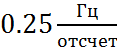 и .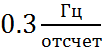

Частота среза фильтра 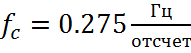, следовательно

Ширина переходной полосы фильтра ,  

2.  Допустимый уровень пульсаций

В децибелах

Такому уровню соответствует окно Ханна (A=-44 дБ)

3.  Определим порядок фильтра: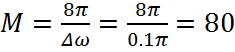

4.  Окно Ханна фильтра:

     

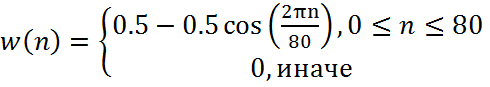
5.  Импульсная характеристика фильтра:

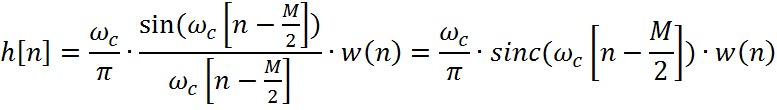
С помощью MATLAB построим график АЧХ фильтра:

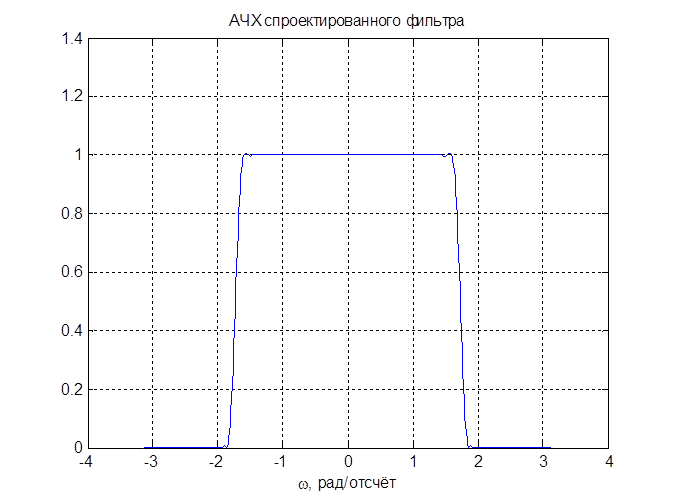
Рис. 11. АЧХ спроектированного фильтра

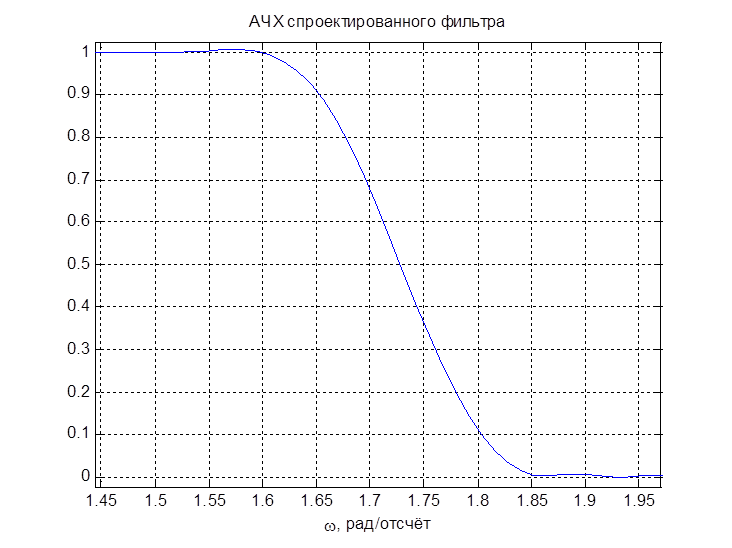
Рис. 12. Увеличенный фрагмент АЧХ

По увеличенному фрагменту на рис. 12 видно, что  соответствуют заданному условию. Уровни пульсаций не превышают заданных значений.

9. Фильтрация сигнала спроектированным фильтром

С помощью следующего кода MATLAB проведем фильтрацию сигнала nspeech2 фильтром, спроектированным в пункте 8

load('speech.mat');

M = 81; n = 0:M-1;

w = 0.5-0.5*cos(2*pi*n/M);

wc = 0.55*pi;

h = w.*(wc*sin(wc.*(n-(M/2))))./(pi*wc*(n-(M/2)));

[H,w] = DTFT(h,512);

y = conv(nspeech2,h);

[Y,w] = DTFT(nspeech2,512);

subplot(211), plot(w,abs(Y)), grid

title ('Амплитудный спектр исходного сигнала');

[Y1,w] = DTFT(y,512);

subplot(212), plot(w,abs(Y1)), grid

title ('Амплитудный спектр сигнала после фильтрации');

xlabel('w');

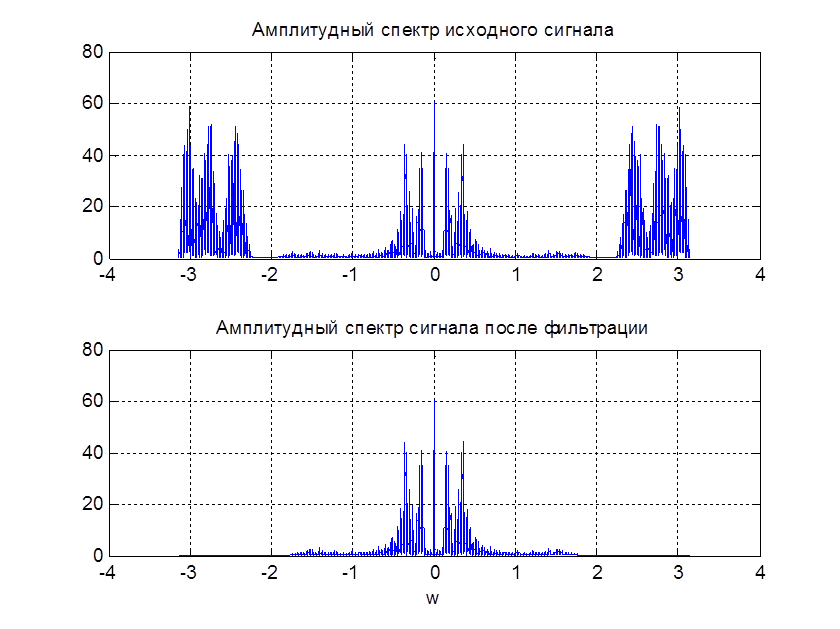
Рис. 13. АЧХ сигнала до и после фильтрации

В результате отфильтрованный сигнал - разборчивая речь без фонового шума, так как частоты полезного сигнала (речи) входят в полосу пропускания нашего фильтра, а шум в полосу задерживания.

10. Расчет КИХ-фильтра с помощью функции fir1

С помощью следующего кода MATLAB рассчитаем фильтр:

b=fir1(80, 0.55, hann(81));

[h,f]=freqz(b,1,256,10000);

w=2*pi*f;

plot(w, abs(h)), grid

title('КИХ - фильтр нижних частот с окном Ханна')

xlabel('Частота,  Гц/отсчет')

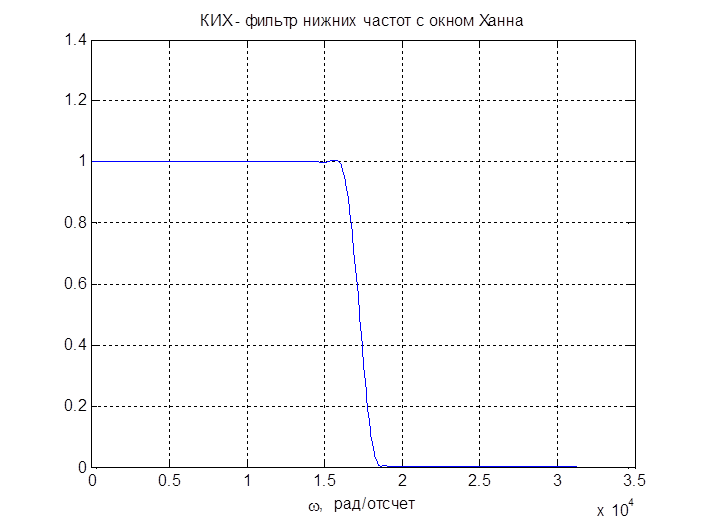
Рис. 14. АЧХ спроектированного фильтра

Видим, что АЧХ на рис. 11 и рис. 14 совпадают, значит функция fir1 была использована правильно. Путем масштабирования логарифмической АЧХ (рис. 15) видим, что спецификация фильтра соблюдена

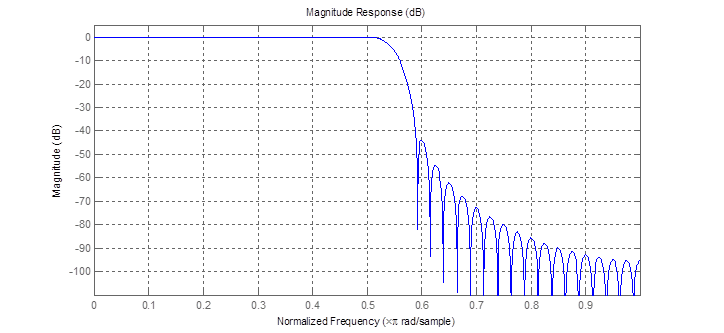
Рис. 15. Логарифмическая АЧХ фильтра

Выводы:

1.  Для реализации идеального ФНЧ его аппроксимируют для физического проектирования КИХ – фильтра путём усечения импульсной характеристики до конечной длины N и сдвига на 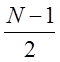. Усеченную и сдвинутую импульсную характеристику можно определить по выражению

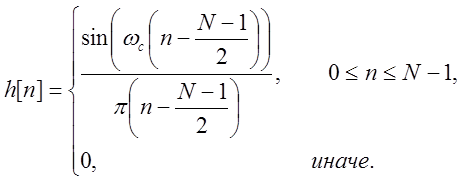
2.  В п. 2 (рис. 2 и 3) было показано, что в результате усечения ИХ у реального фильтра по сравнению с идеальным появляются переходная область и пульсации в полосе пропускания и задерживания, объясняющиеся явлением Гиббса. При увеличении N ширина переходной области уменьшается, амплитуда пульсаций не изменяется, но количество их возрастает (рис. 3 – 5).

3.  Операцию усечения ИХ фильтра можно представить как умножение на оконную функцию. В данной работе были рассмотрены прямоугольное окно, окна Хэмминга, Ханна, Блэкмана (п. 4 – 6). В Matlab для генерации этих окон используются функции hamming, hann, blackman. По амплитудным спектрам окон (рис. 7) можно судить о параметрах фильтра, который можно получить, применив то или иное окно.

4.  Чем шире главный лепесток спектра окна, тем шире переходная полоса фильтра. Амплитуды боковых лепестков влияют на величину пульсаций АЧХ фильтра в полосе пропускания и полосе задерживания.

5.  Окно Кайзера (п. 7) предоставляет более гибкие возможности по сравнению с остальными рассмотренными окнами, т.к. имеет параметр β, с помощью которого можно уменьшать уровень боковых лепестков. На рис. 10 – 12 видно, что с увеличением β окно спадает к нулю более плавно, уровень боковых лепестков уменьшается, но одновременно с этим увеличивается ширина главного лепестка.

6.  В п. 8 был произведён расчёт фильтра, используя окно Ханна. По графикам АЧХ фильтра (рис. 13 – 14) определены параметры полученного фильтра, которые удовлетворяют исходным требованиям. С помощью спроектированного фильтра отфильтрован сигнал speech и результат фильтрации (рис. 16) соответствует АЧХ фильтра (рис. 13).

Источники:

1.  Сайт http://www.dsplib.ru

2.  Лекции по дисциплине «Теория и обработка сигналов» 6 семестр, лектор Щетинин Ю.И.