Изучение методов анализа и синтеза фильтров с конечной импульсной характеристикой. Вариант 2

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

                           Дисциплина  «Теория  и  обработка  сигналов»

ЛАБОРАТОРНАЯ  РАБОТА  № 10

ЦИФРОВЫЕ ФИЛЬТРЫ

С  КОНЕЧНОЙ  ИМПУЛЬСНОЙ  ХАРАКТЕРИСТИКОЙ

Группа: АИ-22                                                                                    Преподаватель:                   Выполнила: Манвейлер М.С.                                                          Щетинин Ю.И.

Вариант: 2                   

Новосибирск, 2005

Цель работы:изучение методов анализа и синтеза фильтров с конечной импульсной характеристикой (КИХ-фильтры,  другое название – нерекурсивные фильтры) с использованием сглаживающих оконных функций.

1.

Построим  в одном графическом окне (используйте subplot) графики импульсной характеристики КИХ-фильтра нижних частот с прямоугольным окном частотой среза для двух значений  длины фильтра  N = 15 и N = 50.

>> N1=15;

>> w=2;

>> n=0:N1-1;

>> h=sin(w.*(n-(N1-1)./2))./(pi.*(n-(N1-1)./2));

>> subplot(211)

>> stem(n,h);

>> N2=50;

>> n=0:N2-1;

>> h2=sin(w.*(n-(N2-1)./2))./(pi.*(n-(N2-1)./2));

>> subplot(212)

>> stem(n,h2);

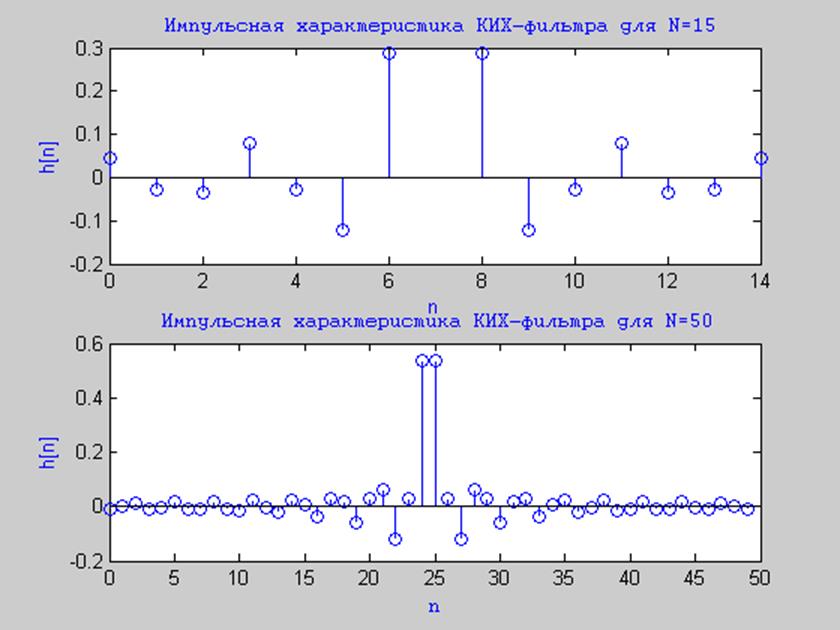
Рис.1 Импульсные характеристики КИХ-фильтров для N=15 и N=50.

Из полученных графиков видно, что чем больше отсчетов берем для построения ИХ, тем больше ее длина и можно более точно воспроизвести вид ИХ.

2.

Используя функцию DTFT, вычислим ДВПФ импульсных характеристик из п.1 и построим графики их АЧХ в линейном масштабе (одно графическое окно) и в децибелах (20*log₁₀(H(e^jω) – другое окно) для 512 отсчетов частоты.  По характеристикам в линейном масштабе определим полосу пропускания, переходную полосу и полосу задерживания фильтра.  

function [X,w] = DTFT(x,M)

% Функция вычисляет значения DTFT от вектора x.

% Обращение

%             [X,w] = DTFT(x,0)

% здесь X - вектор значений DTFT,

% w - вектор угловых частот.

% Если желательно вычислить DTFT с M значениями частоты,

% используется обращение

%             [X,w] = DTFT(x,M)

%

% Этот вариант используется, когда размер вектора x 

% меньше  размера вектора частот w,

% при этом x дополняется нулевыми значениями

N = max(M,length(x));

% Приведение FFT к размеру 2^m

N = 2^(ceil(log(N)/log(2)));

% Вычисление  fft

X = fft(x,N);

% Вектор  частот

w = 2*pi*( (0:(N-1))/N );

w = w - 2*pi*(w>=pi);

% Сдвиг FFT к интервалу от -pi до +pi

X = fftshift(X);

w = fftshift(w);

>> N1=16;

>> n1=0:N1-1;

>> w1=2;

>> h1=sin(w1.*(n1-(N1-1)./2))./(pi.*(n1-(N1-1)./2));

>> [H1,w]=DTFT(h1,512);

>> subplot(211)

>> plot(w,abs(H1))

>> N2=50;

>> n2=0:N2-1;

>> h2=sin(w1.*(n2-(N2-1)./2))./(pi.*(n2-(N2-1)./2));

>> [H2,w]=DTFT(h2,512);

>> subplot(212)

>> plot(w,abs(H2))

в линейном масштабе:

>> subplot(211)

>> plot(w./(2*pi),abs(H1))

>> subplot(212)

>> plot(w./(2*pi),abs(H2))

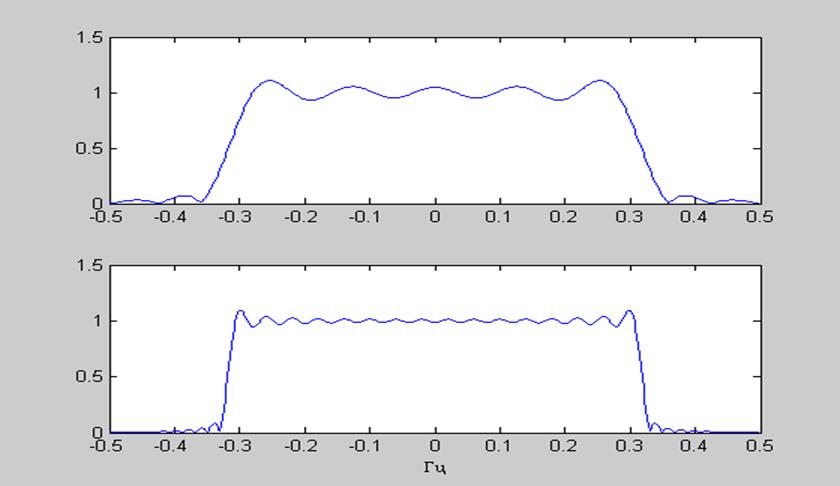
Рис.2 Графики АЧХ для N=16 и N=50 в линейном масштабе.

N=16

Полоса пропускания 0- 0.27 Гц

Переходная область 0.27-0.33Гц

Полоса задерживания  от 0.33 Гц

N=50

Полоса пропускания 0- 0.3 Гц

Переходная область 0.3-0.32Гц

Полоса задерживания  от 0.32 Гц

Нормируем значения АЧХ:

>> subplot(2,1,1);

>> plot(w./(2*pi),abs(H1)./max(abs(H1)))

>> subplot(2,1,2);

>> plot(w./(2*pi),abs(H2)./max(abs(H2)))

>> xlabel('Гц')

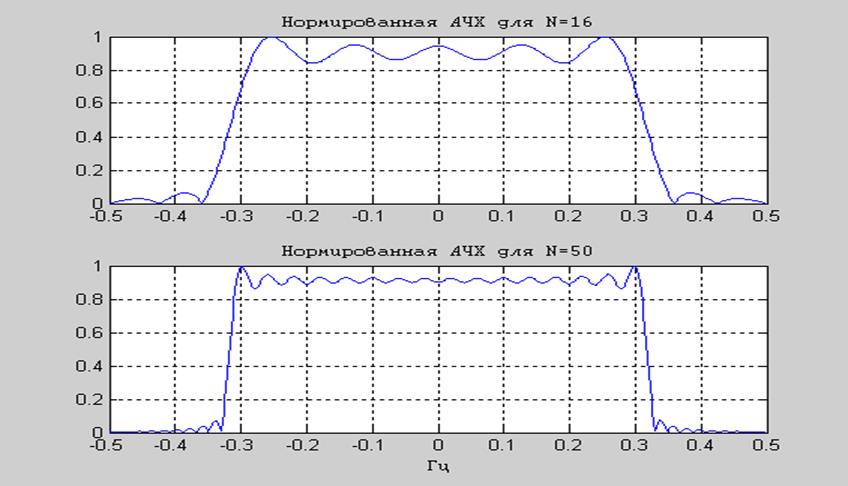
Рис.3 Графики нормированных АЧХ для N=16 и N=50 в линейном масштабе.

В децибелах:

>> subplot(211)

>> plot(w./(2*pi),20*log10(abs(H1)))

>> subplot(212)

>> plot(w./(2*pi),20*log10(abs(H2)))

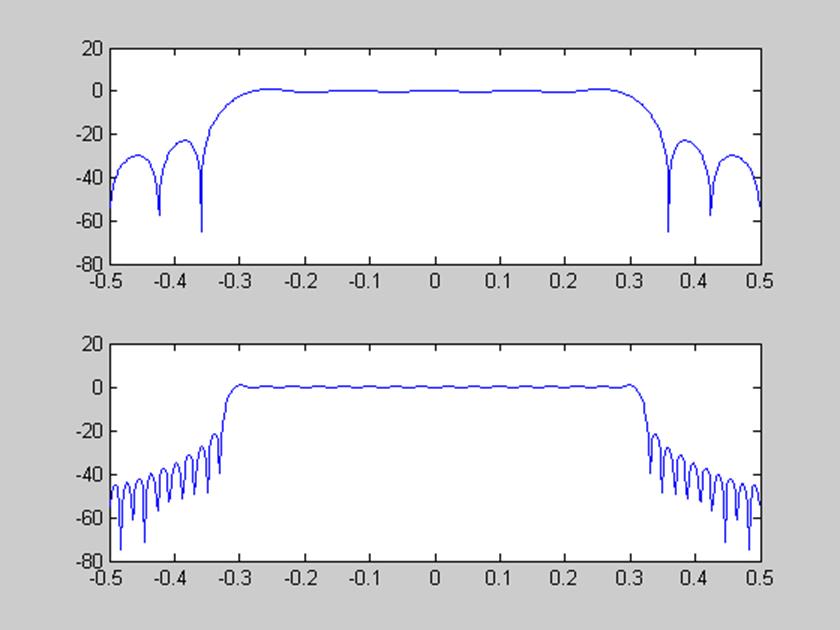
Рис.4 Графики АЧХ для N=16 и N=50 в шкале децибел.

В результате усечения и сдвига ИХ  у реального  фильтра по сравнению с идеальным  появились переходная область и пульсации в полосе пропускания и задерживания.  Пульсации объясняются явлением Гиббса. Чем больше N, тем больше пульсаций. Если увеличить длину фильтра N, то уменьшится  ширина главного лепестка и соответственно ширина переходной области фильтра, но это  не повлияет на уровни боковых лепестков и пульсации в полосах пропускания и задерживания из-за явления Гиббса. 

3.

С помощью функции load() загрузим в рабочее пространство Matlab файл speech.mat. Используя операцию свертки, выполним фильтрацию сигнала speech каждым из двух фильтров.

С помощью функции sound() прослушаем исходный сигнал speech и сигналы после фильтрации.

>> load('speech.mat')

>> y1=conv(nspeech2,h);

>> subplot(211)

>> stem(y1)

>> y2=conv(nspeech2,h2);

>> subplot(212)

>> stem(y2)

>> sound(nspeech2)

>> sound(y1)

>> sound(y2)

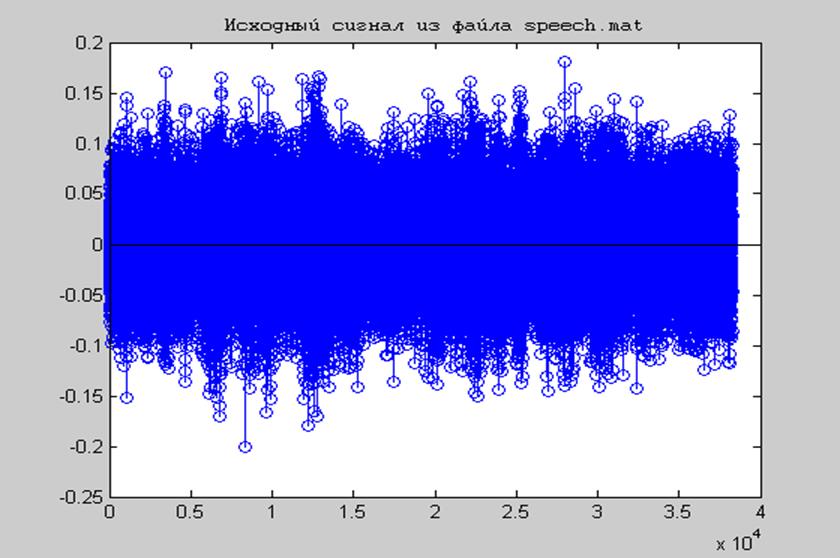
Рис.5 Исходный сигнал из файла speech.mat

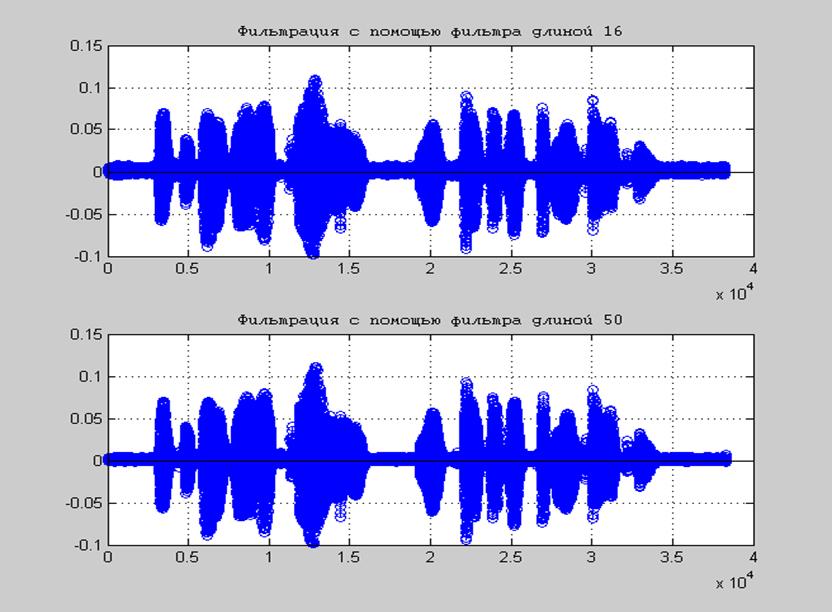
Рис.6 Графики свертки исходного сигнала и импульсной

 характеристики фильтра для N=15 и N=50

Исходный сигнал представлял собой женскую речь с искажением в виде шумов. После фильтрации сигнала speech фильтром размером N=16 качество звучания изменилось – шумы на фоне голоса значительно ослабли. После фильтрации этого же сигнала фильтром размером N=50 – шумы практически исчезли. Из данного эксперимента можно сделать вывод, что чем больше размер фильтра N, тем более эффективно с помощью него осуществляется фильтрация.

Из графиков сигналов также можно увидеть, что исходный сигнал был сильно зашумлен, а после фильтрации уже нет такого наложения шума на звуковом сигнале.

4.

Построим в одном графическом окне графики прямоугольного окна и окон Хэмминга, Ханна, Блэкмана для N = 25. Используя для этого команды Matlab   hamming, hanning, blackman.  

>> N=25;

>> n=1:N;

>> h(n)=1;

>> subplot(411)

>> stem(n,h(n))

>> x=hamming(N);

>> subplot(412)

>> stem(x)

>> y=hanning(N);

>> subplot(413)

>> stem(y)

>> z=blackman(N);

>> subplot(414)

>> stem(z)

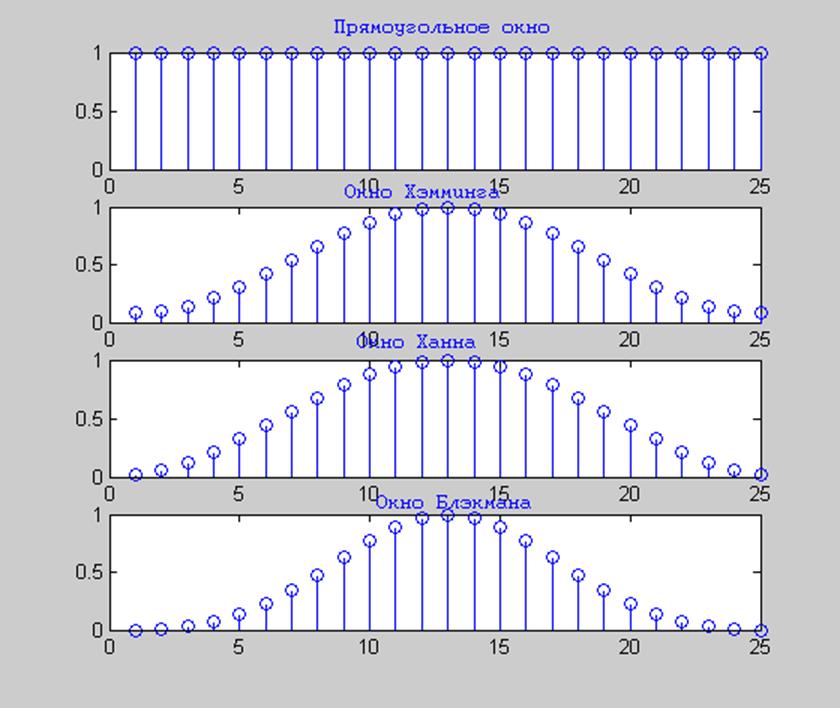
Рис.7 Прямоугольное окно, окна Хэммигна, Ханна и Блэкмана.