Информатика и выч. техника \ Теория и обработка сигналов

Изучение методов анализа и синтеза фильтров с конечной импульсной характеристикой. Вариант 2, страница 2

При синтезе КИХ-фильтров для уменьшения пульсаций АЧХ используется сглаживание импульсной характеристики с помощью специальных функций (окон). Различными авторами предложено достаточно много функций окон, среди которых можно выбрать наиболее подходящее. Конкретное окно тем лучше сглаживает, чем уже у него ширина главного лепестка и чем меньше площади под боковыми лепестками.

5.

Используя функцию DTFT() с 512 частотными отсчетами, вычислим ДВПФ оконных функций из предыдущего пункта и построим в одном окне графики амплитудных спектров в шкале децибел.

>> [H,w]=DTFT(h(n),512);

>> [X,w]=DTFT(x,512);

>> [Y,w]=DTFT(y,512);

>> [Z,w]=DTFT(z,512);

>> subplot(411)

>> plot(w,20*log10(abs(H)))

>> subplot(412)

>> plot(w,20*log10(abs(X)))

>> subplot(413)

>> plot(w,20*log10(abs(Y)))

>> subplot(414)

>> plot(w,20*log10(abs(Z)))

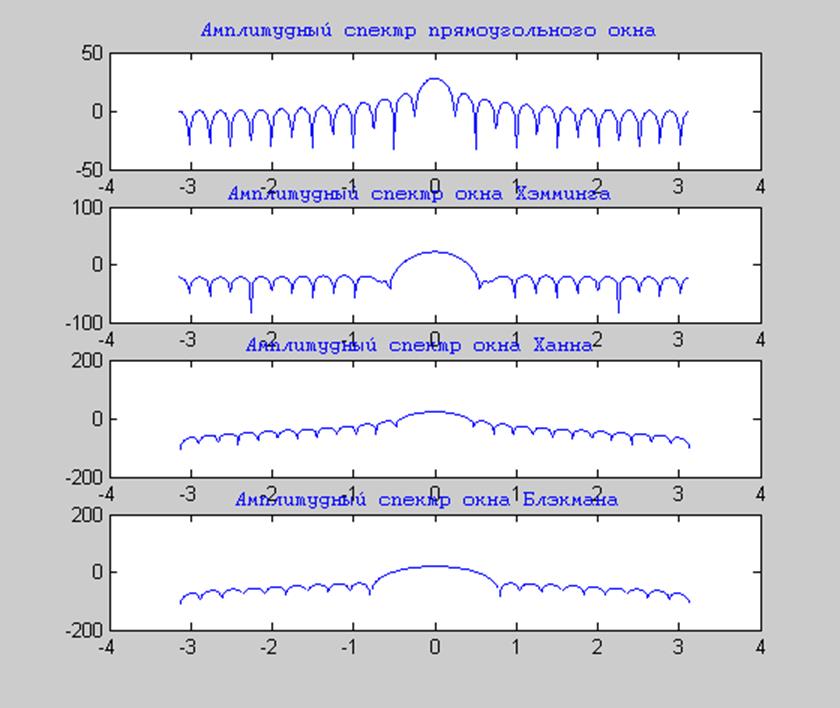
Рис.8 Графики амплитудных спектров окон в шкале децибел.

Как видно из графиков у прямоугольного окна самая маленькая ширина главного лепестка, а самая большая – у окна Блэкмана.

6.

Определим ширину главного лепестка и относительный уровень боковых лепестков в децибелах (относительно амплитуды главного лепестка). Для более точного измерения будем использовать команду zoom. Составим таблицу с измеренными и соответствующими теоретическими значениями величин  и их разностями.

тип окна

ширина главного

лепестка (теоретич.)

ширина главного

лепестка (измер.)

разница

Прямоугольное

0.5

0.5

0

Хэмминга

1

0.96

0.04

Ханна

1

1.1

0.1

Блэкмана

1.57

1.6

0.03

тип окна

относительный уровень

боковых лепестков в дБ

(теоретич.)

относительный уровень

боковых лепестков в дБ

(измер.)

разница

Прямоугольное

-13

-13

0

Хэмминга

-41

-40

1

Ханна

-31

-29

2

Блэкмана

-57

-59

2

7.

Построим графики окон Кайзера  и их амплитудных спектров для  N = 25,  β = 0, β = 1 и  β = 5. Используем для этого функцию Matlab  kaiser(N, beta) и функцию DTFT() с 512 отсчетами частот.

1) β = 0

>> N=25;

>> k1=kaiser(N,0);

>> subplot(211)

>> plot(k1)

>> [K1,w]=DTFT(k1,512);

>> subplot(212)

>> plot(w,abs(K1))

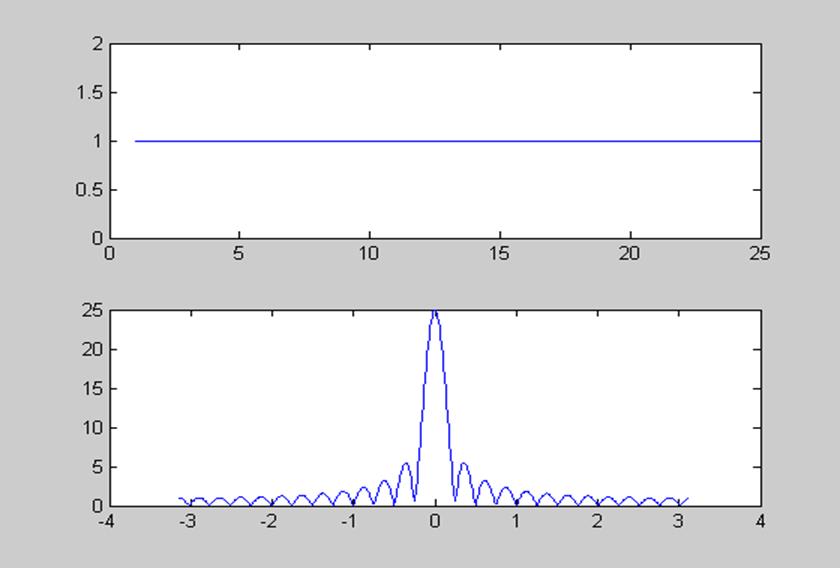
Рис.9 Окно Кайзера и его амплитудный спектр для β = 0.

2)  β = 1

>> k2=kaiser(N,1);

>> subplot(211)

>> plot(k2)

>> [K2,w]=DTFT(k2,512);

>> subplot(212)

>> plot(w,abs(K2))

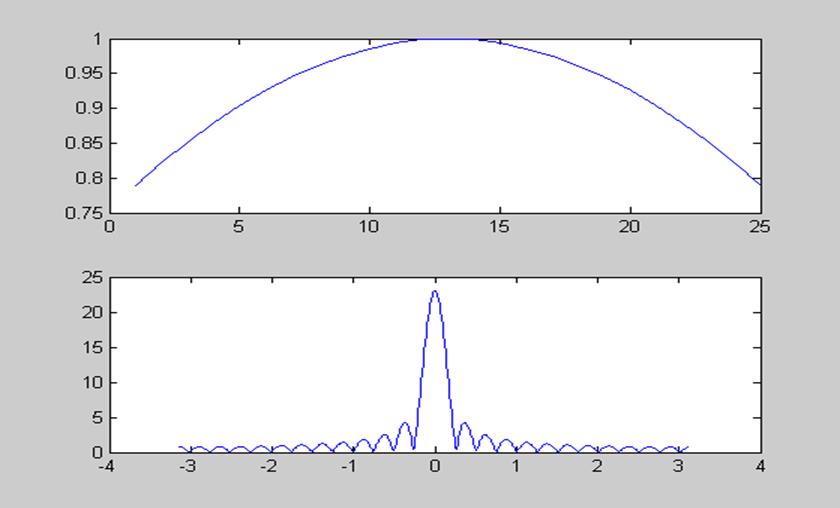
Рис.10 Окно Кайзера и его амплитудный спектр для β = 1.

3) β = 5

>> k3=kaiser(N,5);

>> subplot(211)

>> plot(k3)

>> [K3,w]=DTFT(k3,512);

>> subplot(212)

>> plot(w,abs(K3))

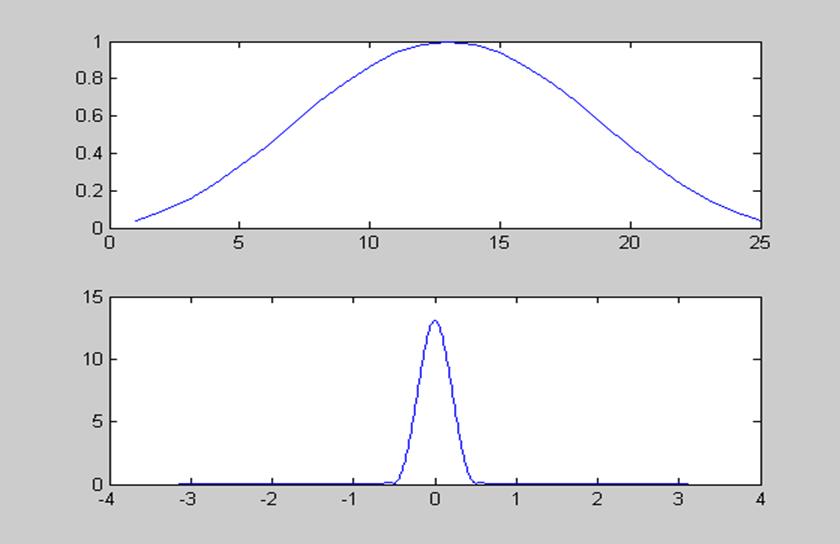
Рис.11 Окно Кайзера и его амплитудный спектр для β = 5.

Более гибкие, по сравнению с другими окнами, возможности предоставляет так называемое окно Кайзера.  - параметр формы окна, с помощью которого можно регулировать амплитуду боковых лепестков и форму окна. При увеличении параметра β форма окна становится более гладкой, и уровень боковых лепестков уменьшается, так, например, при β = 5 он приближается к нулю, но тем шире главный лепесток окна (если при β = 0 она составляет примерно 0.5, то при β = 5 она равна 1 ) и, значит, переходная полоса фильтра.

8. 

Проведем расчет (синтез) фильтра по индивидуальному заданию. Построим в заключение расчета график АЧХ спроектированного фильтра и проверим его соответствие заданию.

График спецификации   фильтра

           

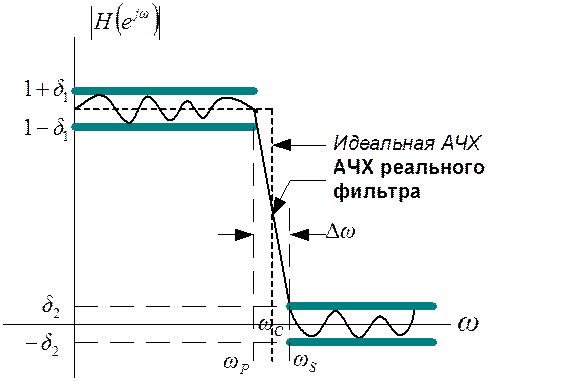
                                               Рис.  П.2.1

             - граничная частота полосы пропускания,

             - граничная частота полосы задерживания, 

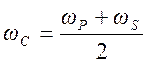 - частота  среза  фильтра,

 - допустимый уровень отклонений (пульсаций) АЧХ в полосе пропускания,

- допустимый уровень отклонений (пульсаций) АЧХ в полосе задерживания.

Пусть заданы следующие исходные требования к фильтру:

· 

· 

·   

· 
Проектирование фильтра заключается в выборе типа окна, определении порядка и коэффициентов (значений ИХ) уравнения фильтра.

1.  Частота среза фильтра 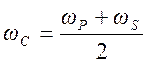 , соответственно  . Нормированная угловая переходная полоса  .

2.  Определим допустимый уровень пульсаций   как  или в децибелах  дБ. Такому уровню ошибки аппроксимации идеальной АЧХ  фильтра соответствует окно Ханна, для которого A = 44 дБ.  Поэтому для дальнейшей реализации фильтра выбираем окно Ханна.

3.  Определяем порядок фильтра с окном Ханна по выражению

                                                          

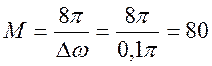
4.  Окно Ханна фильтра
 

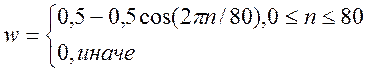
5.  Импульсная характеристика рассчитанного фильтра

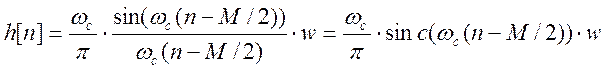
График АЧХ:

>> M=81;

>> wc=0.5*pi;

>> n=0:M;

w=0.5-0.5*cos(2*pi.*n/M);

h=w.*((wc*sin(wc.*(n-(M/2))))./(pi*wc.*(n-(M/2))));

[H,w]=DTFT(h,512);

plot(w,abs(H))

xlabel('paд/c')

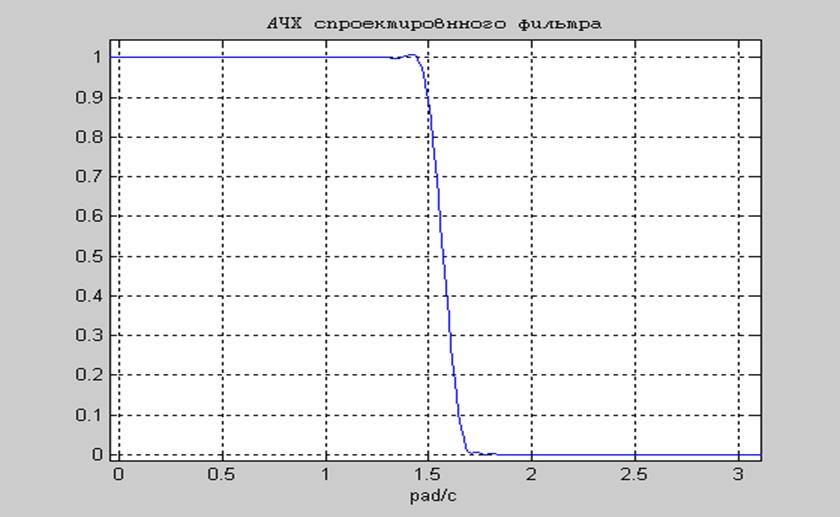
Рис.12 АЧХ спроектированного фильтра.

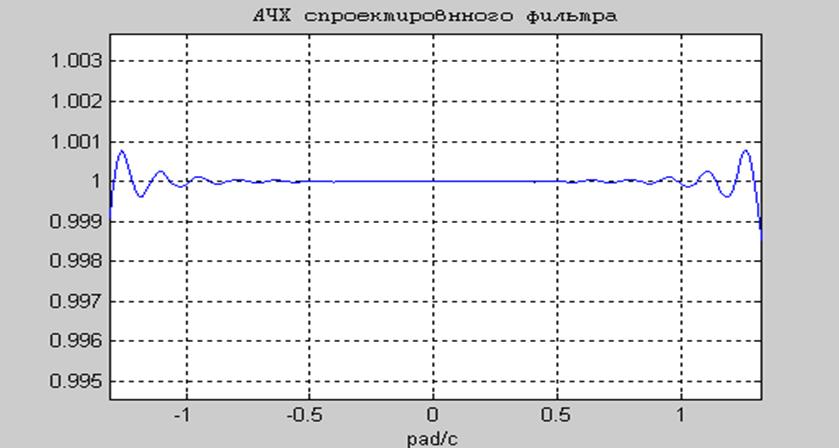
Рис.13 Пульсации в полосе пропускания.

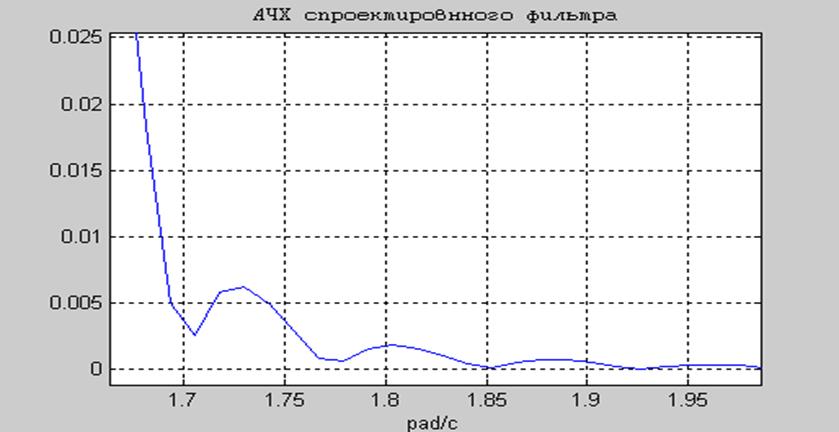
Рис.14 Пульсации в полосе задерживания.

Как видно из графиков, спроектированный фильтр удовлетворяет исходным требованиям:

 - уровень пульсаций в полосе пропускания не превышает δ1 = 0,004;

 - уровень пульсаций в полосе задерживания не превышает  δ2 = 0,008;

 - граничная частота полосы пропускания составляет ωр = 0,45π ≈ 1,413 рад/с;

 - граничная частота полосы задерживания составляет ωs = 0,55π ≈ 1,727 рад/с.

9.

Выполним фильтрацию сигнала speech спроектированным фильтром и оценим качество звучания сигнала до, и после фильтрации.

>> M=81;

>> n=0:81;

>> wc=0.5*pi;

>> h=(0.5-0.5*cos(2*pi*n/80)).*wc/pi.*sinc(wc*(n-M/2));

>> y1=conv(nspeech2,h);

>> stem(y1)

>> sound(y1)

>> sound(nspeech2)

Рис.15 График свертки исходного сигнала и импульсной

 характеристики спроектированного фильтра.

В результате фильтрации спроектированным фильтром в сигнале из файла speech.mat на его фоне не стало слышно шумов. Этот фильтр имеет высокую эффективность фильтрации, но иногда его реализация может оказаться слишком сложной и дорогой, поэтому можно использовать фильтры чуть более низкого порядка, при этом фильтрации также будет достаточно качественной.

Скачать файл