Министерство науки и образования РФ
Новосибирский государственный технический университет
Лабораторная работа № 10
по дисциплине "Теория и обработка сигналов"
Линейные дискретные системы
Выполнил: Преподаватель: к.т.н., доцент
Студент: Макаров С.В. Щетинин Ю.И.
Группа: АИ-92
Факультет: АВТ
Новосибирск
2011
Цель работы: изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем и приобретение практических навыков их анализа в среде Matlab.
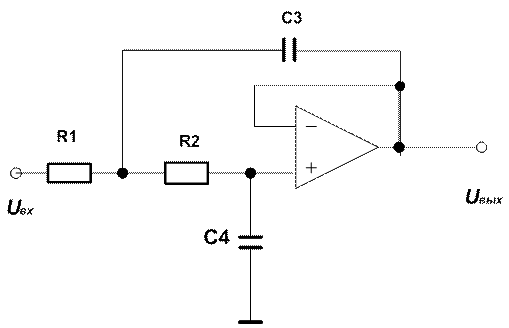
1. Дискретизация аналогового фильтра
Исходные
данные: ФНЧ, 
, R=1000
Ом, С=0,5 мкФ.
|
|
|
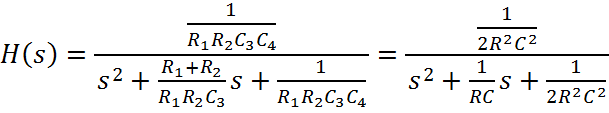
При заданных параметрах АЧХ фильтра имеет вид:
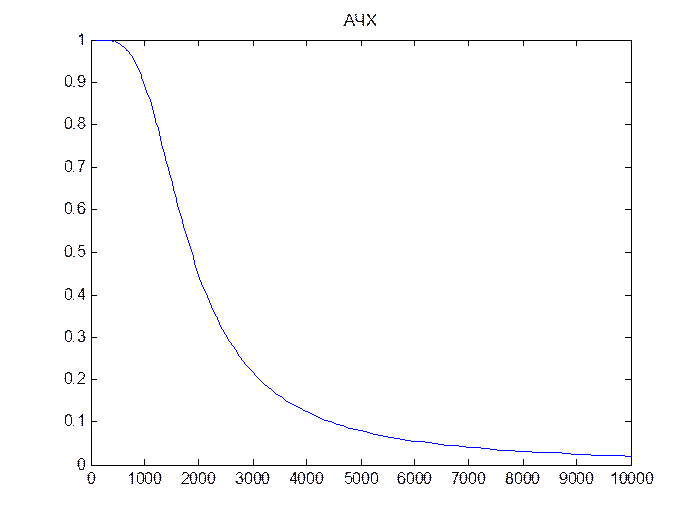
Рис. 2. АЧХ фильтра
По АЧХ видно, что схема представляет
собой ФНЧ, то есть пропускает низкие частоты лучше, чем высокие. Частота среза – это
частота, при которой амплитудная частотная характеристика (АЧХ) снижается до
уровня 
(в децибелах – на 3 дБ) от максимального
значения. Граничная
частота полосы пропускания по уровню 3дБ для такого фильтра определяется из
условия:
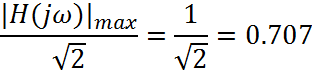
Амплитудному значению 
на АЧХ соответствует частота среза
1414.4 рад/c или 225.2 Гц (рис. 3).
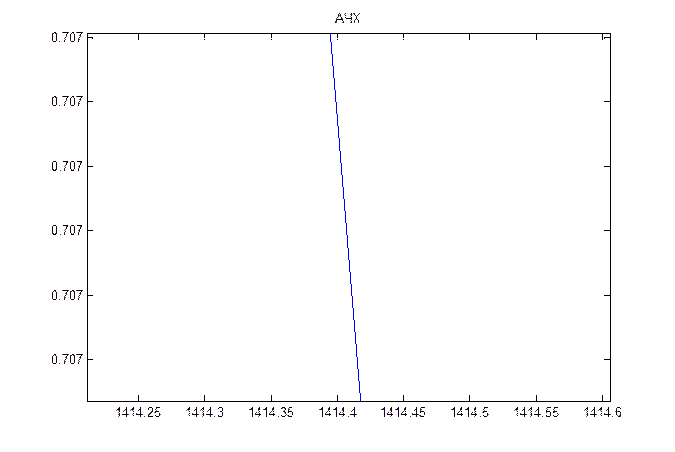
Рис. 3. Увеличенный фрагмент АЧХ фильтра
Введем обозначения: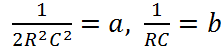 
, тогда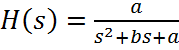 
Запишем по виду передаточной функции дифференциальное уравнение, связывающее выходное и входное напряжения фильтра:
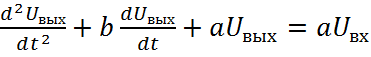(2)
Произведем дискретизацию аналогового фильтра с интервалом отсчетов Δt. Для этого заменим в выражении (2) производную конечной разностью вида
|
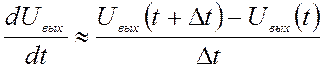
Формула для производной второго порядка через конечные разности
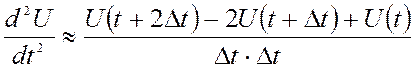
Уравнение (2) преобразовывается к виду:
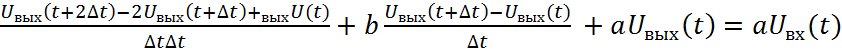
Положим 
и
обозначим 
и
аналогично 
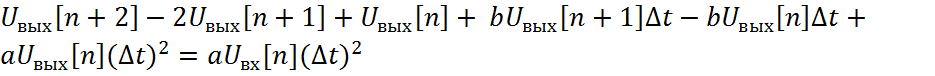(3)
Верхняя граничная частота дискретного
фильтра равна половине частоты отсчетов Fs. Выберем для данного случая
значение Fs = 10 4 Гц, что соответствует
интервалу (периоду) отсчетов 
Подставив в выражение (7) выбранные значения 
, сопротивлений и емкостей и
преобразовав результат, получим разностное уравнение:
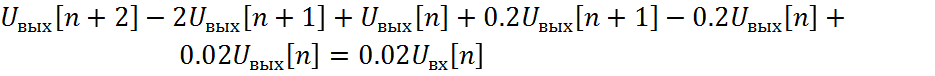(4)
Возьмем Z- преобразование от левой и правой части уравнения (4). С учетом теоремы сдвига получим:
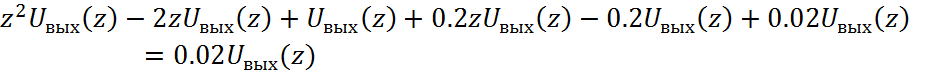
Запишем передаточную функцию дискретного фильтра как отношение Z-преобразований выходного и входного сигналов
|
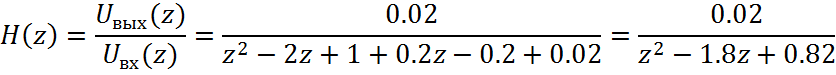
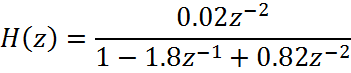
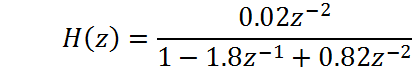
Ниже, на рис.4, приведены АЧХ исходного аналогового и результирующего дискретного фильтра
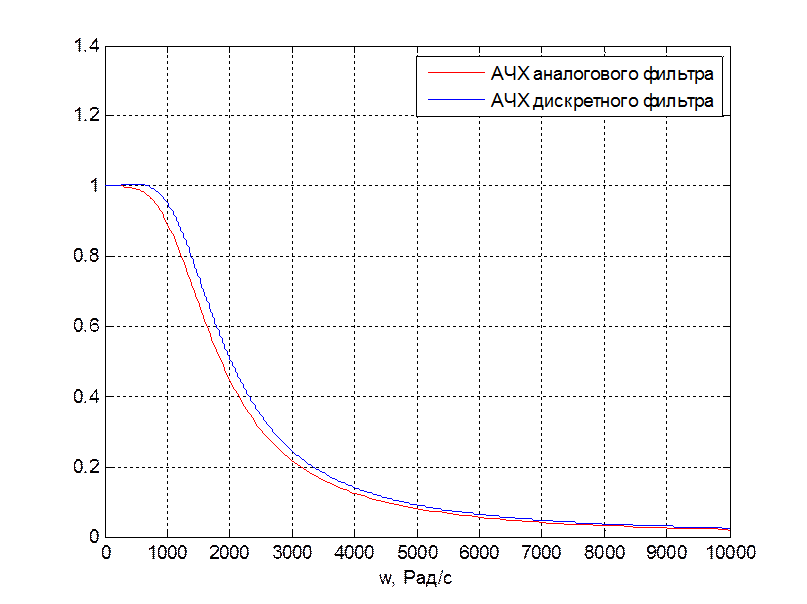
Рис. 4. Графики АЧХ аналогового и дискретного фильтров
На рис. 4 видно, что АЧХ аналогового и дискретного фильтров соответствуют друг другу, но имеют допустимые расхождения. Следовательно, дискретизация фильтра выполнена верно
2. Разложение передаточной функции ДС на простые дроби
Воспользуемся следующей последовательностью команд для определения полюсов, вычетов и коэффициентов целой части.
b=[0.02];
a=[1 -1.8 0.82];
[r,p,k] = residuez(b,a)
Результат:
r =
0.0100 - 0.0900i
0.0100 + 0.0900i
p =
0.9000 + 0.1000i
0.9000 - 0.1000i
k =
[]
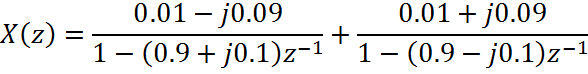
Используя полученное разложение, найдём аналитически импульсную характеристику системы как обратное Z – преобразование от передаточной функции
Построим график импульсной характеристики:
n = 1: 100;
h = (0.01-j*0.09).*(0.9+j*0.1).^n + (0.01+j*0.09).*(0.9-j*0.1).^n;
stem(n, h)
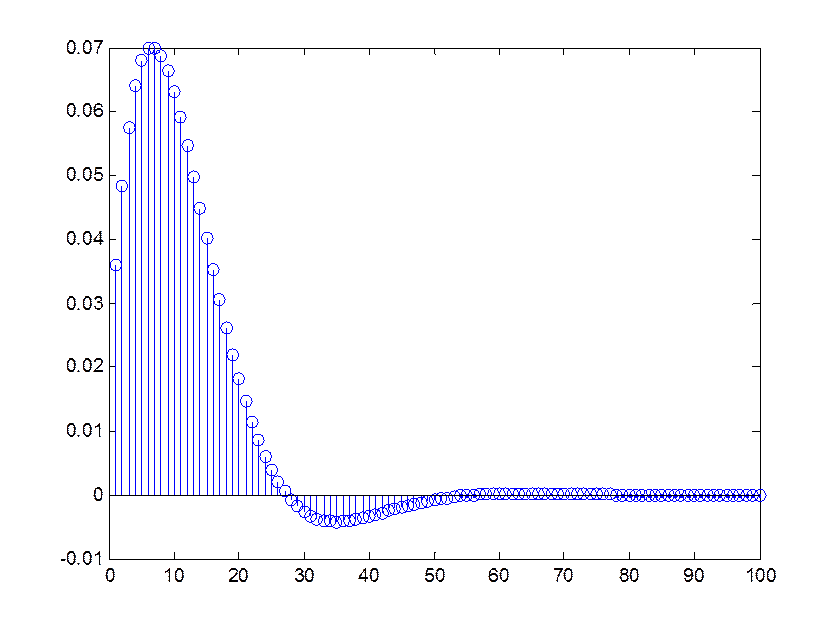
Рис. 5. График аналитически определенной импульсной характеристики
Характеристика системы стремится к константе (нулю), значит система устойчива и для ограниченного входного сигнала получим ограниченный выходной сигнал.
3. Построение диаграммы нулей и полюсов системы
С помощью следующей программы определим нули и полюса системы и построим диаграмму полюсов и нулей:
num = [0.02];
den = [1 -1.8 0.82];
Z = roots(num)
P = roots(den)
zplane(Z, P)
Результат:
Z =
Empty matrix: 0-by-1
P =
0.9000 + 0.1000i
0.9000 - 0.1000i
Система имеет 2 комплексно-сопряженных полюса и не имеет нулей.
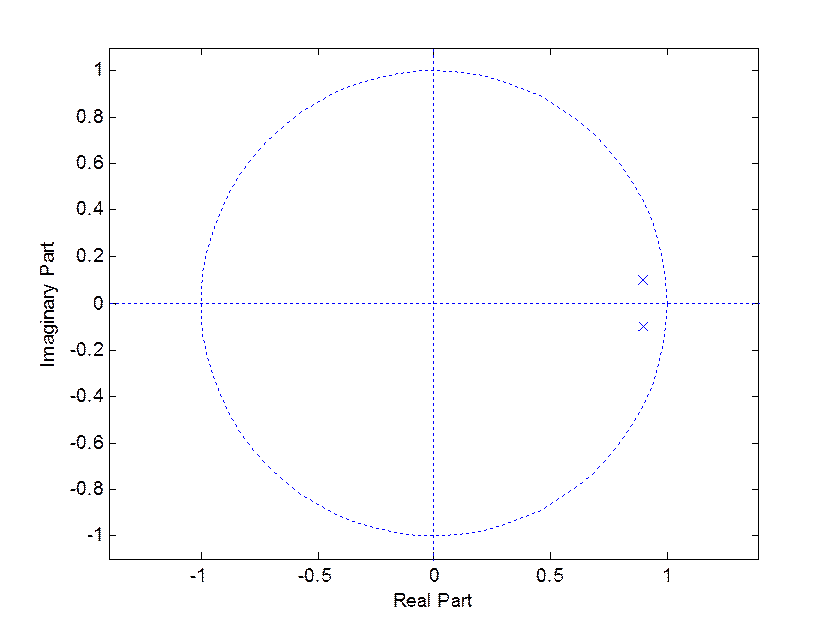
Рис. 6. Диаграмма полюсов и нулей системы
Полюса и нули лежат внутри единичной окружности - система устойчива, что соответствует виду импульсной характеристики (рис. 5).
4. Определение частотной характеристики системы
num = [0.02];
den = [1 -1.8 0.82];
[h,f] = freqz (num, den, 100000, 10^4);
subplot(2,1,1), plot(f, abs(h))
title('АЧХ цифрового фильтра'), grid
subplot(2,1,2), plot(F, angle(H))
title('ФЧХ цифрового фильтра');
xlabel('Частота, Гц'), grid
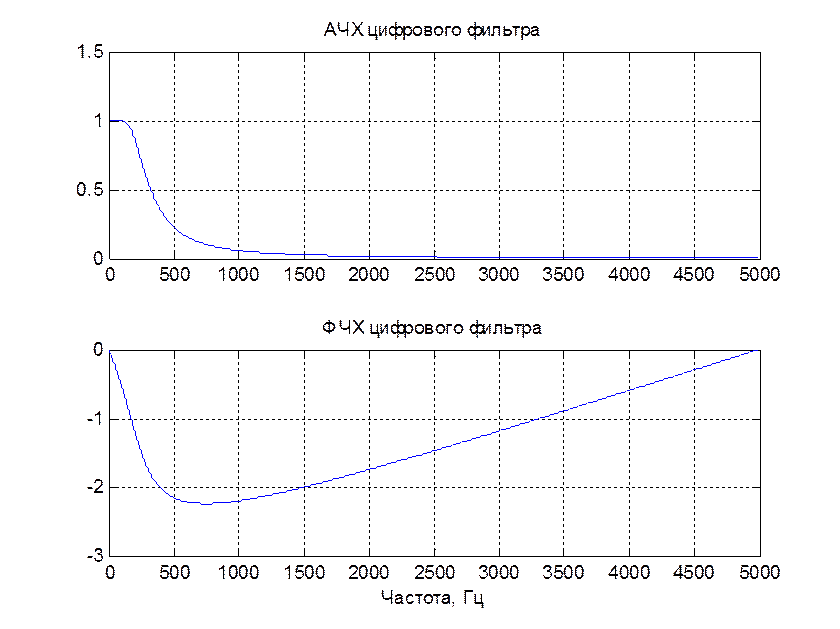
Рис.5.Частотные характеристики ДС
Видим, что система является фильтром нижних частот.
Частота среза 
данного фильтра по уровню 3 дБ равна 249 Гц.
5. Фильтрация сигнала с помощью функции filter()
num = [0.02];
den = [1 -1.8 0.82];
n = 0:0.00001:0.04;
x1 = sin(2*pi*3000*n);
x2 = sin(2*pi*20*n);
x3 = x1 + x2;
y = dlsim(num, den, x3);
subplot(4,1,1);
plot(n, x1);
title('3000 Гц');
subplot(4,1,2);
plot(n, x2);
title('20 Гц');
subplot(4,1,3);
plot(n, x3);
title('Исходная сумма гармоник');
subplot(4,1,4);
plot(n, y);
title('Отфильтрованный сигнал');
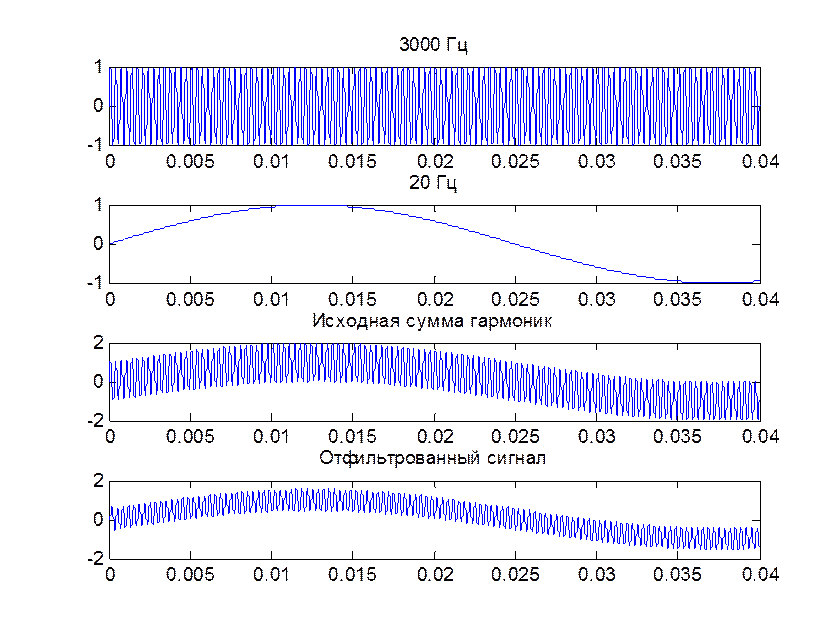
Рис. 8. Иллюстрация применения цифрового фильтра
6. Исследование влияния расположения нулей и полюсов на частотную характеристику системы
1) Возьмем полюса с противоположными знаками:
Z = []; P = [ -0.9-j*0.1 ; -0.9+j*0.1 ];
zplane(Z, P)
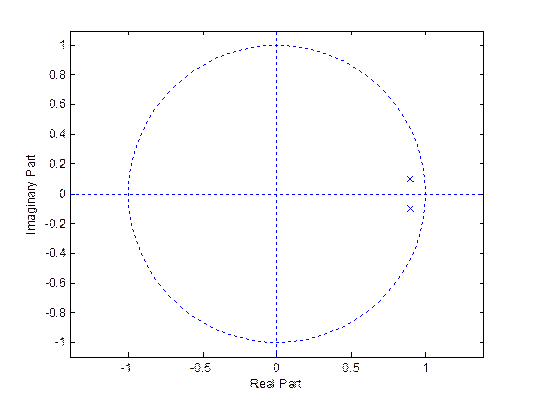
Рис. 9. Диаграмма нулей и полюсов
Z = []; P = [ -(0.9+j*0.1) ; -(0.9-j*0.1) ];
[num,den]=zp2tf(0,P, 1);
freqz(num,den,1000,10000)
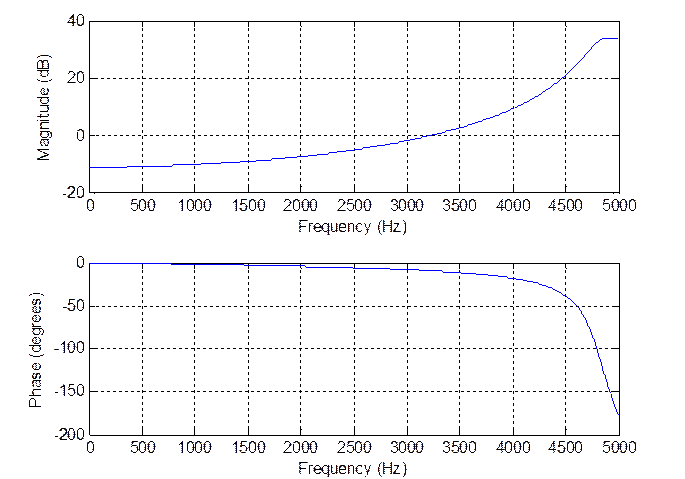
Рис. 10. АЧХ и ФЧХ системы
Получили фильтр верхних частот
2) Возьмем полюса 0.5 + j0.1 и 0.5 - j0.1
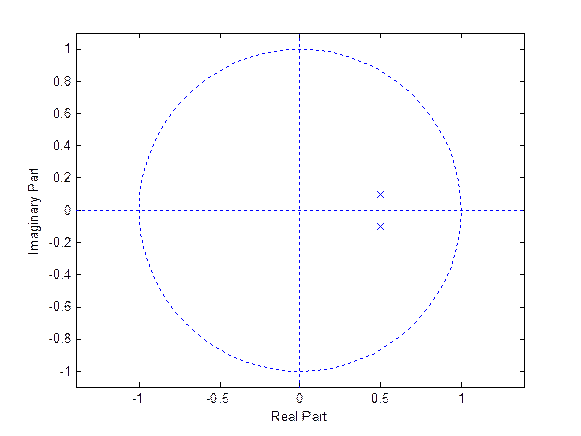
Рис. 11. Диаграмма нулей и полюсов
Z = []; P = [ (0.5+j*0.1) ; (0.5-j*0.1) ];
[num,den]=zp2tf(0,P, 1);
freqz(num,den,1000,10000)
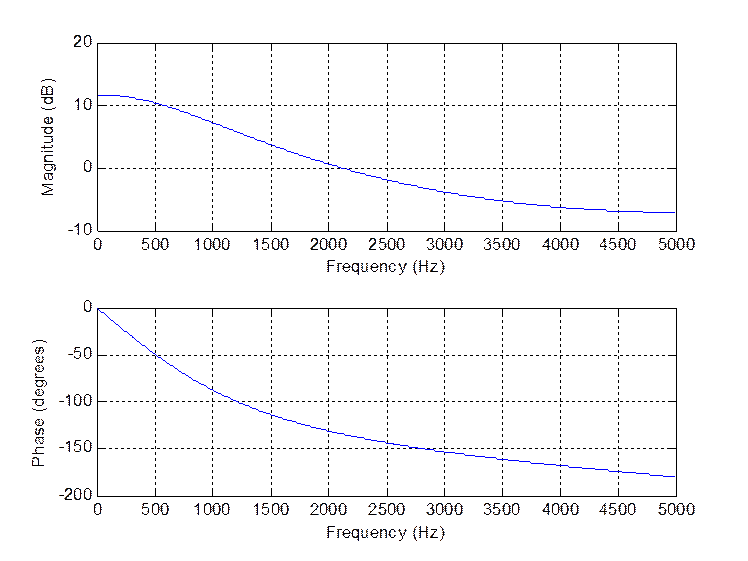
Рис. 12. АЧХ и ФЧХ системы
При уменьшении действительных частей полюсов получили ФНЧ с более пологими частотными характеристиками
7. Определение импульсной характеристики системы с помощью функций impz() и dimpulse()
num = [0.02]; den = [1 -1.8 0.82];
[H,T] = IMPZ(num,den, 100);
figure(1), stem(T, H)
title('Импульсная характеристика');
xlabel('n');
figure(2), dimpulse(num, den, 100)
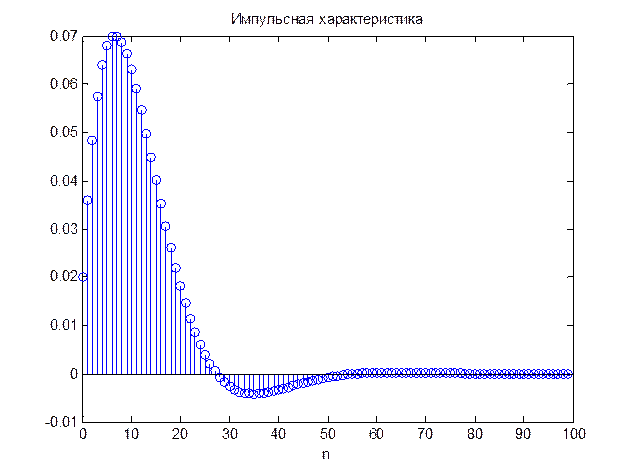
Рис. 13. Импульсная характеристика системы, найденная с помощью impz()
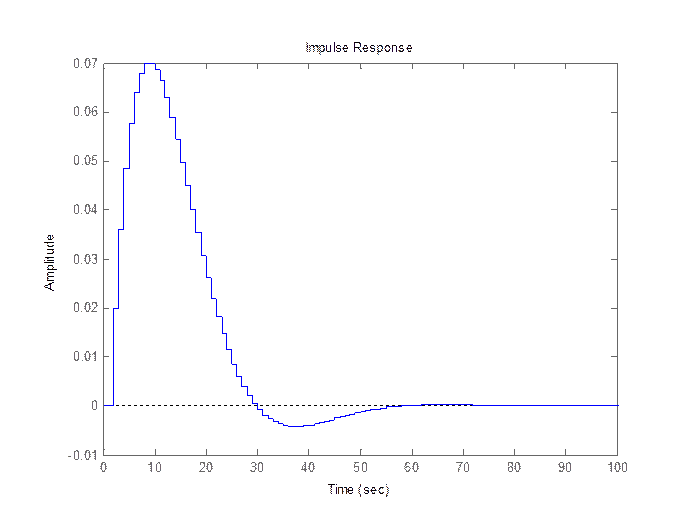
Рис. 14. Импульсная характеристика системы, найденная с помощью dimpulse().
Графики импульсных характеристик на рис.13 и рис. 14 совпадают с графиком аналитически определенно импульсной характеристики (рис. 5).
8. Построение графика переходной характеристики фильтра с помощью функции dstep()
num = [0.02];
den = [1 -1.8 0.82];
dstep(num, den, 100)
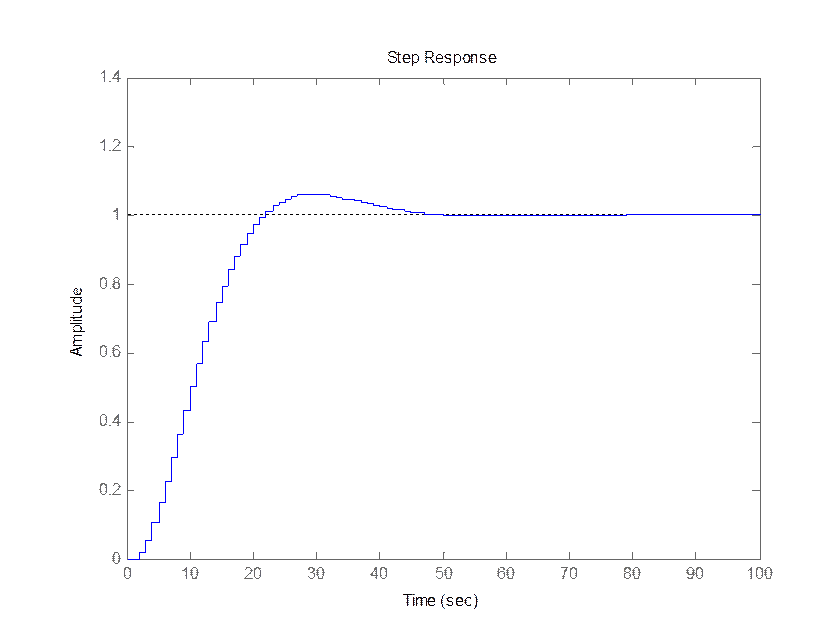
Рис. 15. Переходная характеристика системы, найденная с помощью dstep().
Переходная характеристика – это реакция системы на входной сигнал в виде единичной последовательности при нулевых начальных условиях. Её можно определить через импульсную характеристику:
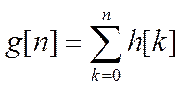
Это можно подтвердить, проанализировав импульсную и переходную характеристики нашей системы (рис. 5, 13, 14 и рис. 15)
Выводы:
1. Дискретные линейные стационарные системы описываются линейными разностными уравнениями с постоянными коэффициентами. Разностное уравнение, описывающее дискретную систему можно получить из дифференциального уравнения, задающего аналоговую систему, с помощью процедуры дискретизации
Такую процедуру мы провели в пункте 1 и проанализировали ее результаты: АЧХ дискретной системы сходится с АЧХ аналоговой системы, которую мы дискретизировали (наглядно видно на рис. 4)
2. Характеристикой систем в области переменной z является передаточная функция, которая определяется как отношение Z - преобразований выходного и входного сигналов.
В пункте 1 мы получили передаточную функцию ДС, использовав обратное Z-преобразование для линейного разностного уравнения системы.
3. Импульсной характеристикой системы
является выходной сигнал системы при подаче на её вход функции 
.
В пункте 2 лабораторной работы мы нашли импульсную характеристику ДС как обратное Z-преобразование передаточной функции системы, что делается аналитическим способом.
В MATLAB для нахождения импульсной характеристики можно использовать функции impz() и dimpulse(). Их работу мы изучили и продемонстрировали в пункте 7
4. Передаточную функцию можно определить зная расположение нулей и полюсов исследуемой системы в z-плоскости.
5. АЧХ и ФЧХ системы характеризуют изменение амплитуды и фазы гармоники соответственно при прохождении через систему
В пункте 4, с использованием функции freqz(), мы нашли АЧХ и ФЧХ исследуемой системы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
-
величина шага приращения времени (интервал дискретизации)