Изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем. Вариант 8

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

Дисциплина  «Теория  и  обработка  сигналов»

ЛАБОРАТОРНАЯ  РАБОТА  № 9

Линейные дискретные системы

Группа:АТ-53

Вариант: 8                                                                                                        Преподаватель: Щетинин Ю.И.

Студенты :  Ездакова Е.

Дашиев Т.                          

2008

Цель работы:изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем и приобретение практических навыков  их анализа в среде Matlab.

1.  Дискретизация аналогового фильтра.

       

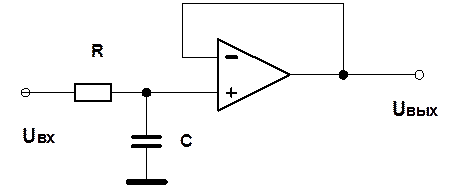
Рис.1. Схема активного ФНЧ.

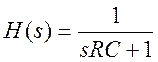   ,    R=1кОм, С=1 мкФ

Передаточная функция фильтра имеет вид:

.

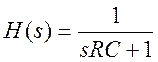
Для R=1 кОм  C=1 мкФ АЧХ фильтра имеет вид:

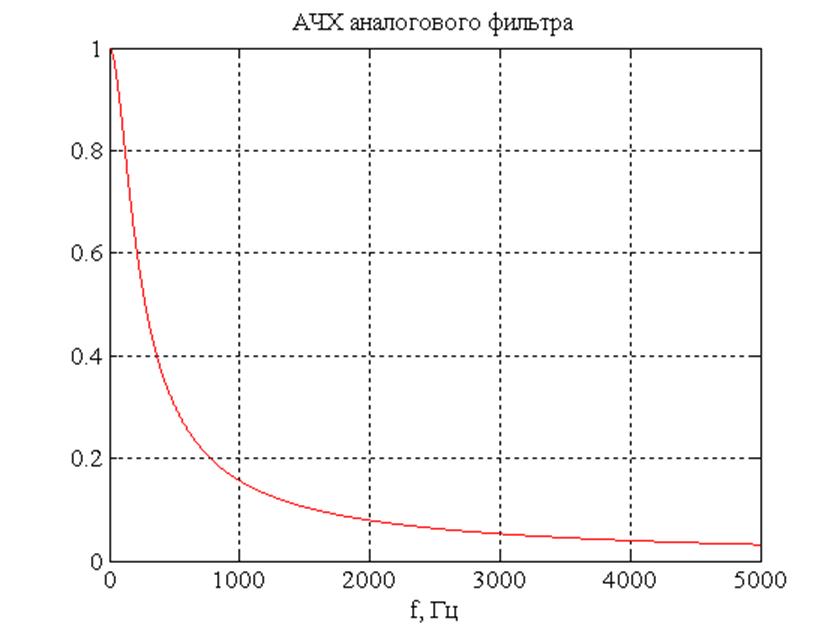
Рис.2.  АЧХ  активного фильтра.

Пусть RC=a.

Запишем  по виду передаточной функции дифференциальное уравнение, связывающее выходное и входное напряжения фильтра

.

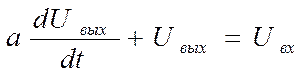Произведем дискретизацию аналогового фильтра с интервалом отсчетов  Δt.

Для этого заменим производную конечной разностью вида ,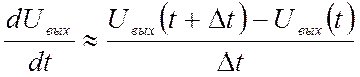

где   – величина шага приращения времени (интервал отсчетов, или интервал дискретизации).

При этом уравнение преобразовывается к виду

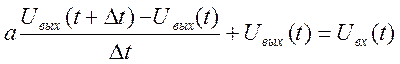
Положим    и обозначим  , аналогично .

Тогда выражение приобретает вид

.

Верхняя граничная частота дискретного (цифрового) фильтра равна половине частоты отсчетов (дискретизации)  F_s.  Выберем для данного примера значение  F_s = 10 ⁵ Гц, что соответствует интервалу (периоду) отсчетов     

Для выбранных числовых значений  уравнение перепишем в форме

.

После преобразования

.

Возьмем  Z- преобразование от левой и правой части уравнения. С учетом теоремы сдвига получим

.

Теперь запишем передаточную функцию дискретного фильтра как отношение Z - преобразований выходного и входного сигналов

.

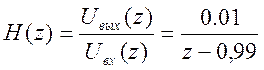Частотная характеристика  дискретной системы представляет собой передаточную функцию при , т.е.  .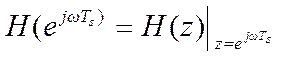

f=0:1:5000;

T = 10^(-5);

H1=-1./(0.001*j*2*pi*f+1)

H2 = 0.01./((exp(2*pi.*f*j*T))-0.99);

figure(1)

hold on

plot(w,abs(H1),'r','LineWidth',3,'LineStyle','- -')

plot(f,abs(H2),'b','LineWidth',2)

set(gca,'FontName','Times New Roman Cyr','FontSize',12)

title('АЧХ аналогового фильтра')

xlabel('f, Гц')

legend('АЧХ аналогового фильтра','АЧХ дискретного фильтра')

grid on

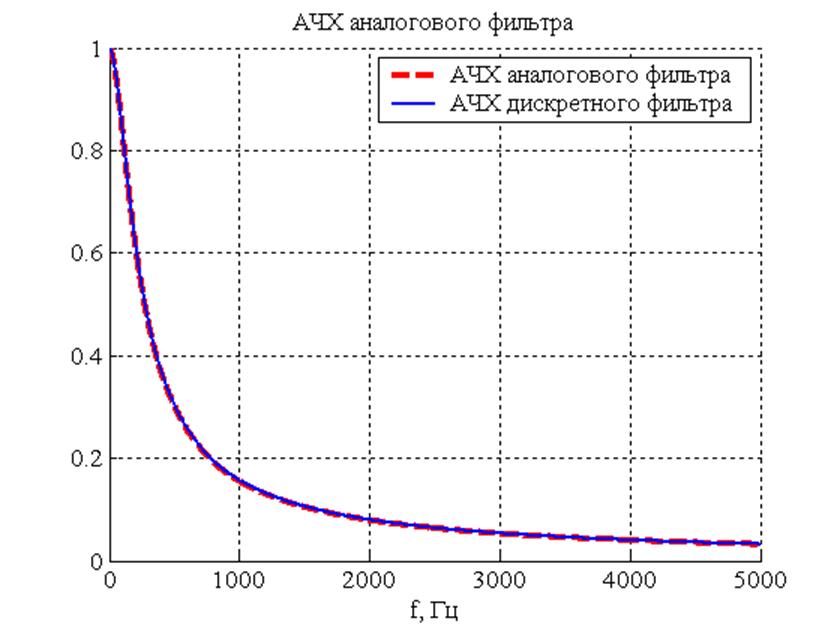
Рис.3.  АЧХ аналогового и дискретного фильтров.

Комментарии: из графиков АЧХ аналогового и дискретного сигнала видно, что они практически совпадают, что говорит о том, что дискретизация прошла верно.

2.  Передаточная функция системы, нахождение импульсной характеристики системы.

Передаточная функция:   .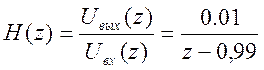

Вектор коэффициентов числителя: num=[0.01].

Вектор коэффициентов знаменателя:  den=[1 -0.99].

B=[0,01];

A=[1 -0,99];

[R,P,K]=RESIDUEZ(B,A)

R =        0 - 0.0503i

 0 + 0.0503i

P =          0 + 9.9499i

               0 - 9.9499i

K =        []

Для исходной передаточной функции с учетом полученных результатов получим следующее разложение на простые дроби:

.

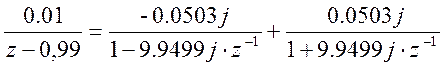Импульсная характеристика системы:

                                                      

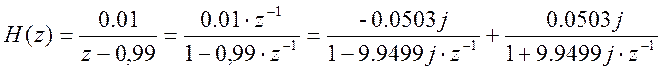
Найдя обратное Z-преобразование, используя :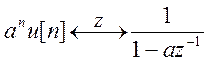

n = 0:1:500;

h = 0.01*(0.99).^(n-1);

plot(n,h)

set(gca,'FontName','Times New Roman Cyr','FontSize',12)

title('Импульсная характеристика цифрового фильтра')

xlabel('n')

grid

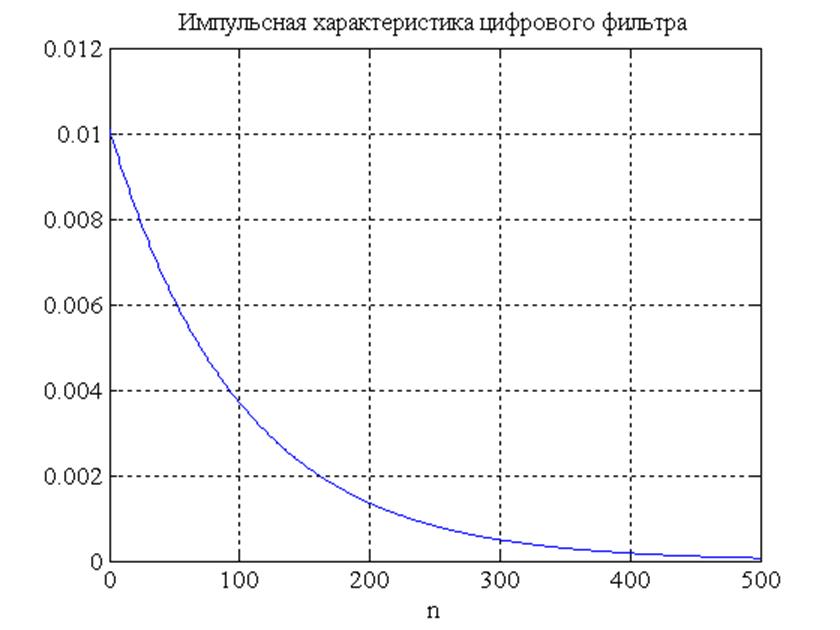
Рис.4.   Импульсная характеристика цифрового фильтра.

Комментарии: передаточная функция и импульсная характеристика  дискретной системы связаны между собой Z-преобразованием, а именно  . Что позволяет при известной передаточной функции найти импульсную характеристику.

3. Нахождение нулей и полюсов дискретной системы при помощи функции roots(). Построение диаграммы нулей и полюсов системы.

Определение нулей и полюсов фильтра с помощью встроенной функции :

B=[0,01];

A=[1 -0,99];

x = roots(B)

y = roots(A)

x =   Empty matrix: 0-by-1

y =   0 + 9.9499i

         0 - 9.9499i

Построение диаграммы нулей и полюсов фильтра:

num=[0.01];

den=[1 -0.99];

zplane(num,den)

В данном случае нули отсутствуют, и существует один полюс в точке (0.99 , j0 ).

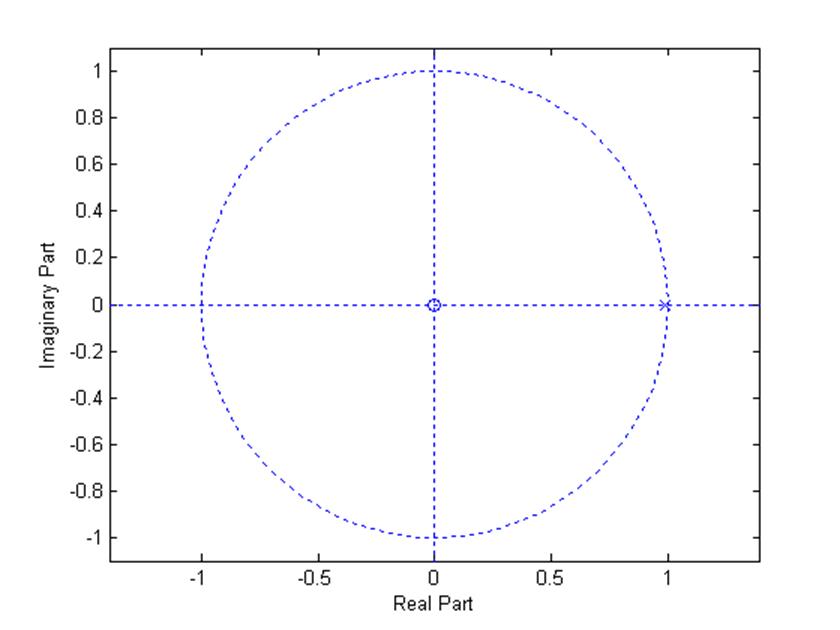
Рис.5. Диаграмма нулей и полюсов.

Комментарии: корни многочлена – числителя передаточной функции являются нулями, а корни знаменателя – полюсами. Для того чтобы система была устойчивой полюса должны располагаться только внутри круга единичного радиуса, причем в левой полуплоскости.В нашем случае система устойчива, так как полюс находится в левой полуплоскости окружности.

4. Расчет частотной характеристики системы и построение графиков её АЧХ и ФЧХ при помощи функции freqz. Определение частоты среза  АЧХ по уровню 3 дБ.

num=[0.01];

den=[1 -0.99];

freqz(num, den,1000,10^5)

subplot(211)

set(gca,'FontName','Times New Roman Cyr','FontSize',10)

title('АЧХ системы')

xlabel('Частота,Гц')

subplot(212)

set(gca,'FontName','Times New Roman Cyr','FontSize',10)

title('ФЧХ системы')

xlabel('Частота,Гц')

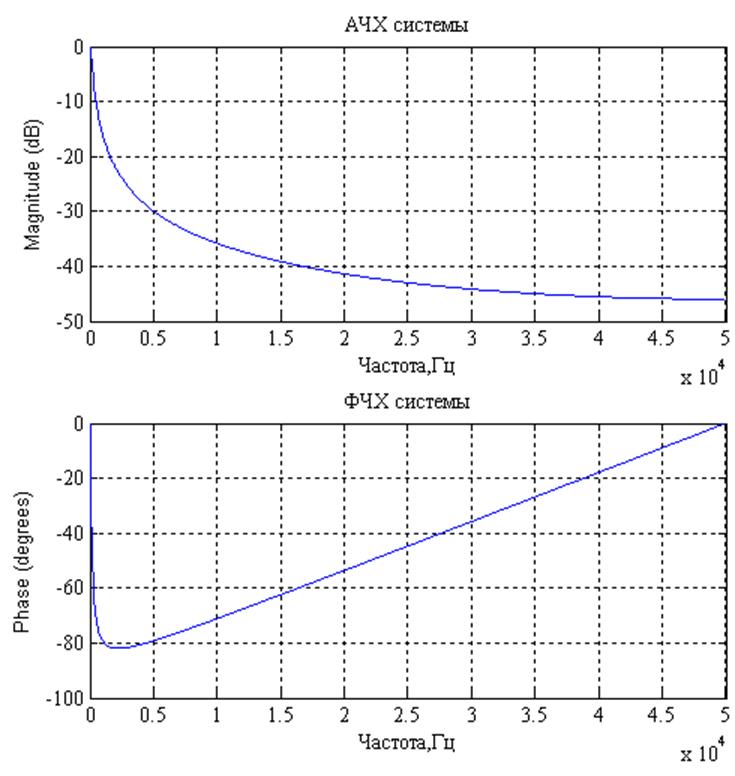
Рис.6.  АЧХ и ФЧХ системы.

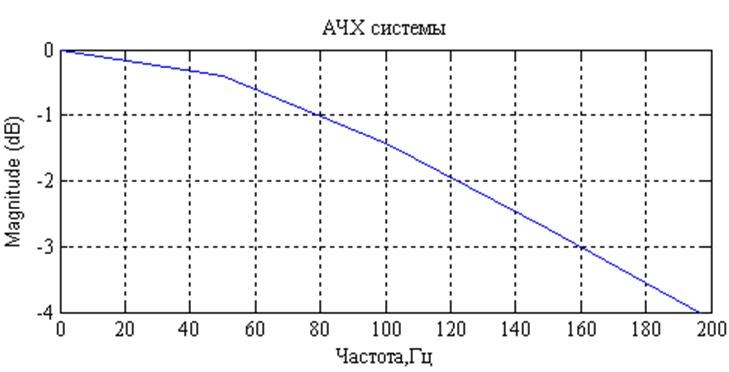
Рис. 7. АЧХ дискретного  фильтра (увеличенный масштаб).

Как видно из рисунка 7 частота среза по уровню 3дб равна 160 Гц.

Комментарии: модуль частотной характеристики показывает изменение амплитуды дискретной гармоники при прохождении её через систему и называется амплитудно–частотной характеристикой (АЧХ) дискретной системы.Аргумент отражает изменение фазы гармоники и является фазочастотной характеристикой (ФЧХ) системы.

5. Фильтрация гармонических сигналов.

n=0:0.00001:0.2;

subplot(4,1,1)

x=cos(2*pi*50*n); plot(n,x,'LineWidth',2)

set(gca,'FontName','Times New Roman Cyr','FontSize',12), legend('Сигнал с частотой 50 Гц')

subplot(4,1,2)

y=cos(2*pi*250*n); plot(n,y,'LineWidth',2)

set(gca,'FontName','Times New Roman Cyr','FontSize',12),legend('Сигнал с частотой 250 Гц')

subplot(4,1,3)

z=x+y; plot(n,z,'LineWidth',2)

set(gca,'FontName','Times New Roman Cyr','FontSize',12), legend('Сумма двух сигналов')

num=[0.01];

den=[1 -0.99];

subplot(4,1,4), F=filter(num,den,z); plot(n,F,'LineWidth',2)

set(gca,'FontName','Times New Roman Cyr','FontSize',12), legend('Сигнал на выходе фильтра ')

xlabel('Число отсчетов,N')

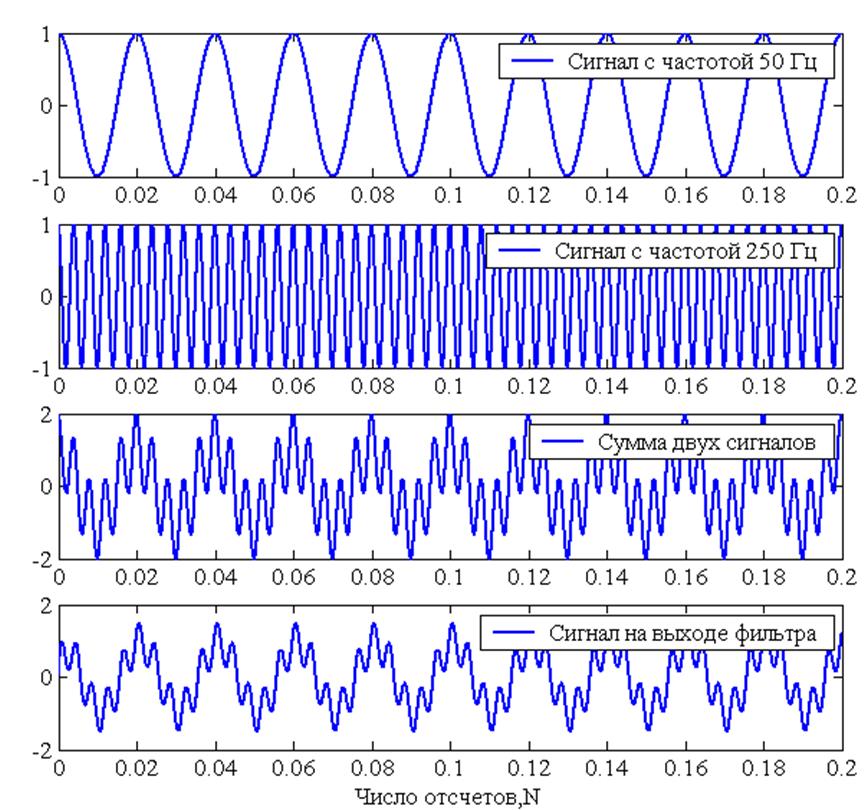
Рис.8.  Исходные сигналы, их сумма и сигнал после фильтрации.

Видно,  что    ФНЧ выделяет низкочастотные составляющие из входного

 сигнала

6. Исследование влияния расположения нулей и полюсов на частотную характеристику системы. Построение АЧХ системы по её передаточной функции.

p =  0.99.

[[num,den]=zp2tf(0,0.99,0.01);

freqz(num,den,1000,100000)

Передаточная функция системы: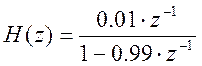

Изменим знак у полюса, теперь p=-0.99:

Передаточная функция системы: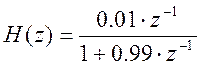

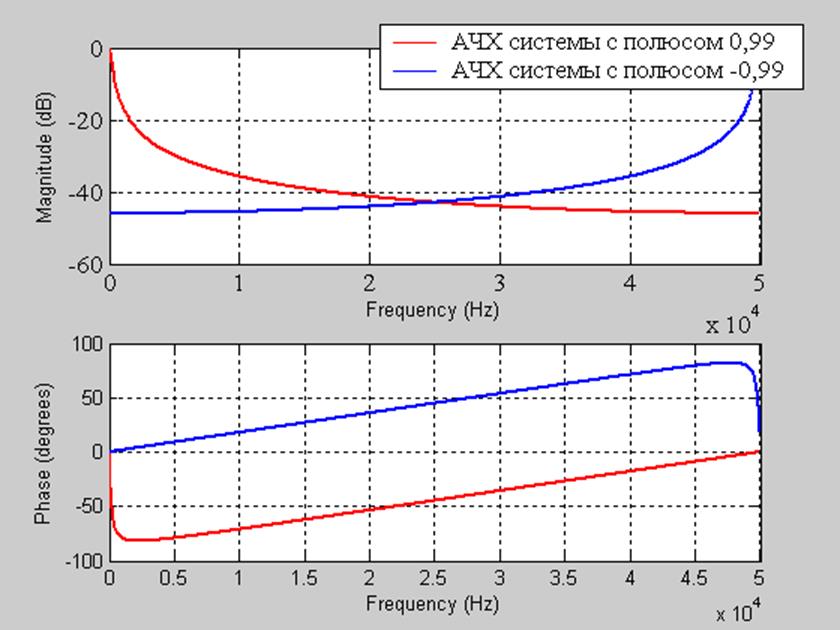
Рис.9. АЧХ с полюсом p = 0.99(красный график) и АЧХ с полюсом p = -0.99(синий график).

Комментарий: как видно из графиков на рис.9. при изменении  у полюса знака с положительного на отрицательный система трансформируется из ФНЧ  в ФВЧ.

Пусть у системы 2 симметричных полюса:

[num,den]=zp2tf(0,[0.4,-0.4],-0.9);

[num1,den1]=zp2tf(0,[0.4*j,-0.4*j],-0.9);

subplot(211)

hold on

freqz(num,den,1000,100000)

freqz(num1,den1,1000,100000)

set(gca,'FontName','Times New Roman Cyr','FontSize',10)

legend('Пара действительных полюсов дают АЧХ режекторного фильтра','Пара мнимых полюсов дают АЧХ полосового фильтра')

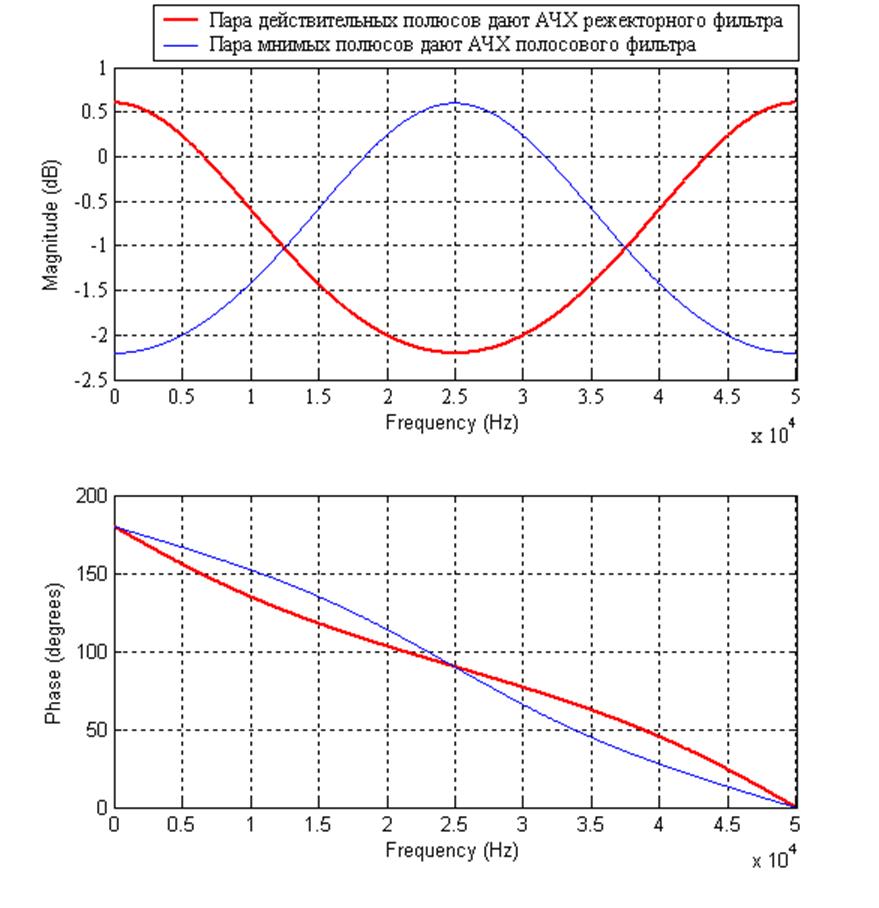
Рис.10.  АЧХ с полюсами p1 = 0.4 и p2 = -0.4 (красный график) и АЧХ с полюсами p1 = 0.4*j и p2 = -0.4*j (синий график).

Комментарий: если система имеет 2 действительных полюса, противоположных по знаку, то АЧХ системы соответствует режекторному фильтру, и чем ближе эти полюса к 1 по модулю, тем шире полоса задерживания такого фильтра, и наоборот. Если система имеет 2 мнимых полюса, противоположных по знаку, то АЧХ системы соответствует полосовому фильтру, и чем ближе эти полюса к 1 по модулю, тем уже полоса пропускания фильтра, и наоборот.

7. Определение импульсной характеристики системы и построение её графика при помощи функций impz() и dimpulse().

num=[0,01];

den=[1,-0.99];

impz(num,den,350)

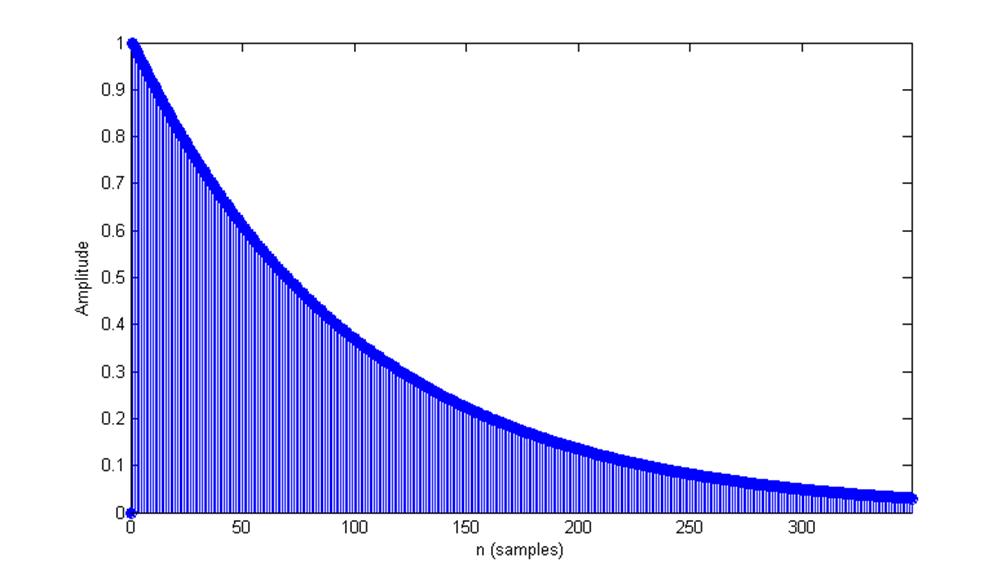
Рис.11. Импульсная характеристика, полученная с помощью функции impz().

num=[0,01];

den=[1,-0.99];

dimpulse(num,den,350)

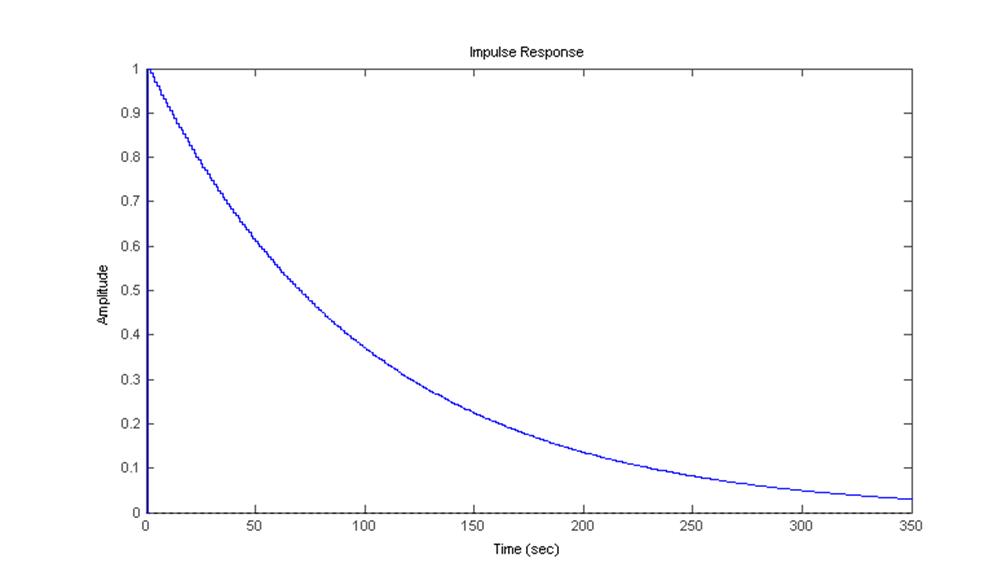
Рис.12. Импульсная характеристика, полученная с помощью функции dimpulse().

Комментарий:  графики импульсных характеристик, полученных с помощью функций impz() и dimpulse() совпадают с импульсной характеристикой цифрового фильтра.

Рис.13.   Импульсная характеристика цифрового фильтра.

8. Построение графика переходной характеристики фильтра  с помощью функции dstep().

num=[0,01];

den=[1,-0.99];

dstep(num,den,350)

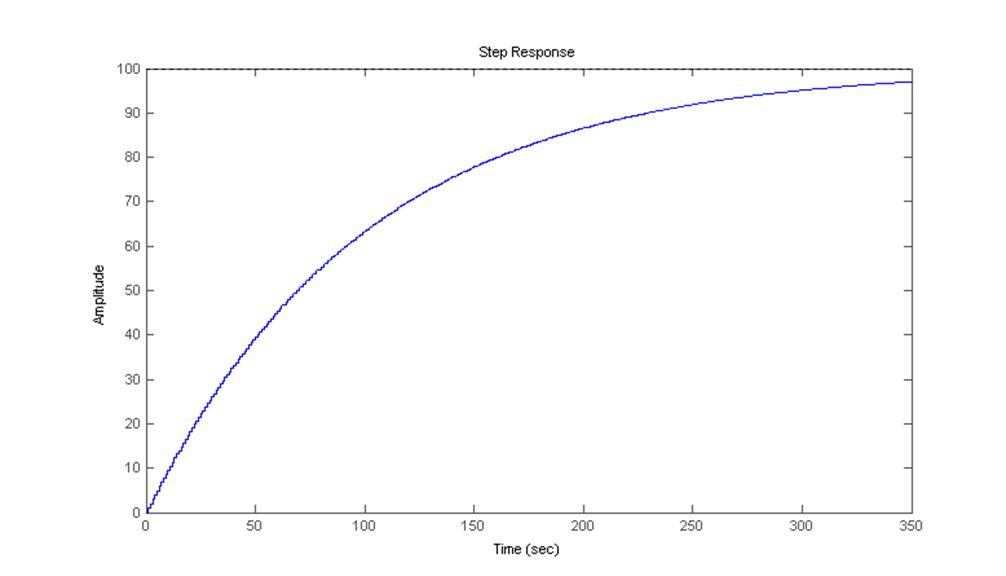
Рис.14.  Переходная характеристика фильтра.

Комментарии: переходная характеристика – реакция (отклик) системы на входной сигнал в виде единичной последовательности при нулевых начальных условиях.

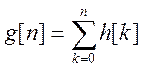 - переходная характеристика равна сумме импульсных характеристик.

Выводы по работе:

• Цифровой фильтр можно получить путем дискретизации аналогового, при этом АЧХ цифрового фильтра будет соответствовать АЧХ аналогового, но следует учитывать, что верхняя граничная частота  дискретного фильтра, в отличие от аналогового,  ограничена частотой Найквиста,  равной половине частоты отсчетов.
• Частотную характеристику системы можно получить при помощи передаточной функции путем перехода .
• От передаточной функции можно перейти к временным характеристикам: импульсной и переходной.
• Расположение полюсов и нулей передаточной функции очень важно, изменение полюсов может привести к изменению его параметров, типа фильтра .