МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
ЛАБОРАТОРНАЯ РАБОТА № 11
СЛУЧАЙНЫЕ СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ
по дисциплине
«Теория и обработка сигналов»
Выполнили:
Студентки
Факультета АВТ
Группы АО-21
Рогова Татьяна
Яшина Оксана
Преподаватель:
Доц. Ю. И. Щетинин
Новосибирск-2005
СЛУЧАЙНЫЕ СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ
Цель работы:изучение основных характеристик стационарных случайных сигналов (среднего значения, автокорреляционной функции, спектральной плотности мощности) и приобретение практических навыков их вычисления и анализа в среде Matlab.
1. Генерация 500 отсчетов случайного сигнала X с нулевым математическим ожиданием и единичной дисперсией с использованием функции randn(). Построение графика X. Вычисление оценок среднего и дисперсии случайного сигнала X с помощью Matlab-функции и сравнение полученных оценок с теоретическими значениями.
Случайной функцией называют функцию, которая для определенного значения аргумента (аргументов) представляет собой случайную величину. Случайные сигналы представляются как случайные процессы (функции).
Математическое ожидание (среднее значение) случайного процесса X(t) – это неслучайная функция mx(t), значения которой при определенном значении аргумента t равно математическому ожиданию соответствующего сечения процесса, т.е.
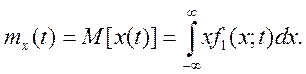 Для
момента времени tk математическое ожидание можно получить, взяв
мгновенные значения N реализаций, сложив эти значения, разделив на число
реализаций и перейдя к пределу при N→∞
Для
момента времени tk математическое ожидание можно получить, взяв
мгновенные значения N реализаций, сложив эти значения, разделив на число
реализаций и перейдя к пределу при N→∞ 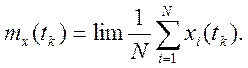
Придавая t все возможные значения, получим функцию mx(t), которая является результатом усреднения значений случайного процесса по множеству реализаций.
Характеристикой разброса реализаций относительно математического ожидания является дисперсия Dx(t), которая выражается через одномерную плотность распределения следующей формулой:
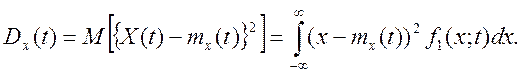
Дисперсия имеет размерность квадрата случайного процесса X(t), например, для случайного напряжения это B2. Дисперсию можно определить также через средний квадрат (начальный момент второго порядка) M[X2(t)] случайного процесса, а именно
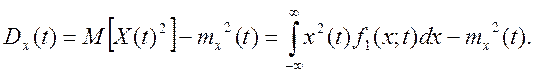
Вместо дисперсии во многих случаях используется среднее квадратичное отклонение
![]()
которое имеет размерность самого случайного процесса и поэтому оказывается более удобным.
Сгенерируем случайный сигнал X с 500 отсчетами:
X=randn(1,500);
plot(X)
title('Casual signal, N = 500')
Вычисление математического ожидания и выборочной дисперсии с помощью встроенных в Matlab функций mean() и var():
S=mean(X)
S = 0.0353
D=var(X)
D = 1.0072
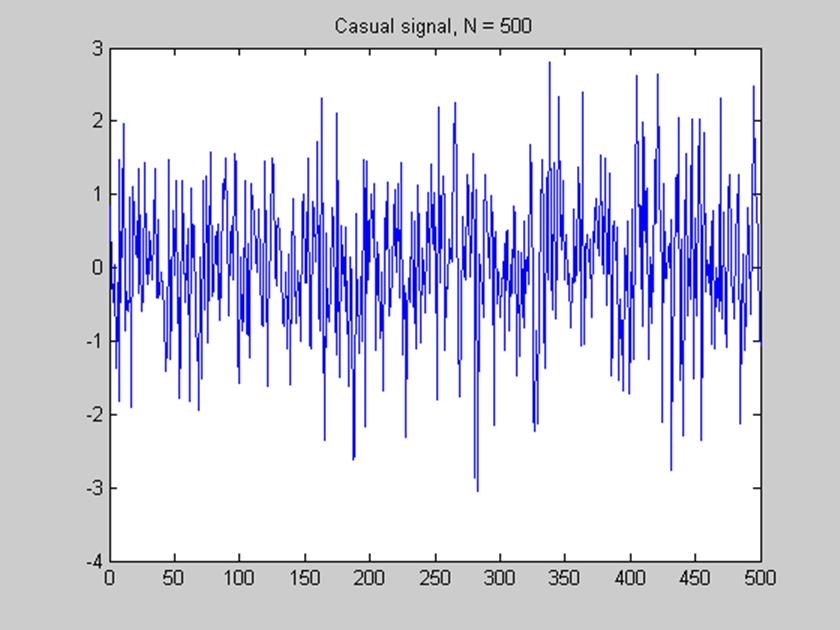
Рис.1. Случайный сигнал Х с 500 отсчетами с нулевым математическим
ожиданием и единичной дисперсией.
Matlab-функция для вычисления оценок среднего и дисперсии случайного сигнала:
function [mat,disp] = Estimation(N)
X=randn(1,N);
sum=0;
for i=1:N,
sum=sum+X(i);
end
mat=sum/N;
sum1=0;
for i=1:N,
sum1=sum1+power((X(i)-mat),2);
end
disp=sum1/(N-1);
Применение функции:
>> [mat,disp] = Estimation(500)
mat = 0.0173
disp = 0.9598
Полученные нами значения оценки среднего и дисперсии отличаются от теоретических, так как являются результатом одного опыта, в то время как теоретические значения являются результатом усреднения значений случайного процесса по множеству реализаций (конкретных функций, которые дает отдельный опыт).
На практике определяют оценку по конечному числу реализаций, поэтому точность оценивания возрастает с увеличением количества реализаций.
2. Построение на одной фигуре, применяя subplot, графиков плотности вероятности нормальной случайной величины из п. 1 и график гистограммы сигнала X с помощью функции hist() с числом интервалов 15 – 20.
x=-4:0.1:4;
f=(1/sqrt(2*pi*var(X))).*exp(-1*power(x-mean(X),2)./(2*var(X)));
subplot(2,1,1)
plot(x,f)
title('Graph to density to probability')
subplot(2,1,2)
hist(X,20)
axis([-4, 4, 0, 80])
title('Graph histogram')
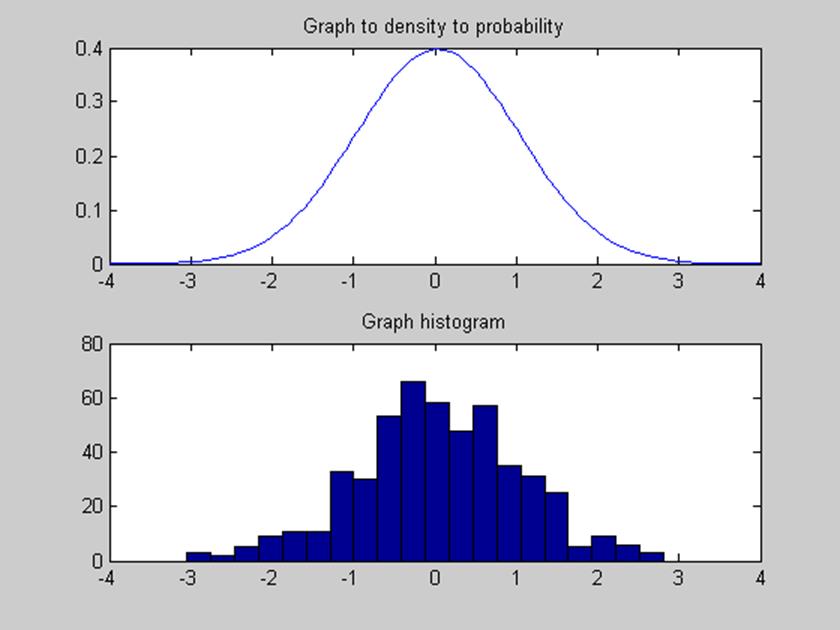
Рис. 2. Графики плотности вероятности и гистограммы
случайной величины Х с 500 отсчетами
Первый график отражает вероятность появления того или иного значения в сигнале и представляет собой кривую, площадь под которой равна 1, а второй график отражает частоту встречаемости каждого значения. График плотности вероятности показывает, с какой вероятностью появится значение, а гистограмма показывает частоту появления этого значения.
Частота и вероятность являются почти одинаковыми характеристиками в том случае, если количество опытов стремится к бесконечности. Если же количество опытов ограничено, то эти величины будут иметь различный характер. Иными словами, вероятность - это частота при бесконечном числе наблюдений.
3. Выражение автокорреляционной функции (АКФ) случайного
дискретного сигнала и объяснение смысла корреляционной зависимости для сигнала.
Аналитическое определение АКФ выходного сигнала для системы с уравнением ![]() при
входном сигнале в виде белого шума с АКФ
при
входном сигнале в виде белого шума с АКФ
![]() , при этом
, при этом ![]() - дисперсия (мощность) шума,
- дисперсия (мощность) шума, ![]() - единичный дельта-импульс, используя
выражение связи между АКФ выходного
- единичный дельта-импульс, используя
выражение связи между АКФ выходного ![]() и входного
сигналов
и входного
сигналов ![]() линейной дискретной системы
линейной дискретной системы
![]() , где h[m]-
импульсная характеристика.
, где h[m]-
импульсная характеристика.
Важной статистической характеристикой поведения случайного сигнала является его автокорреляционная функция (АКФ). Для стационарного в широком смысле (СШС) дискретного случайного процесса Xn автокорреляционная функция определяется выражением
![]()
при этом АКФ для СШС процессов не изменяется с изменением временного аргумента n, а зависит только от расстояния (сдвига) m.M – это оператор математического ожидания, т.е. усреднения. Функция kXX[m] – четная функция своего аргумента m. АКФ определяет, как сильна связь между отсчетами сигнала, разделенными друг от друга интервалом m. Ясно, что для реальных случайных сигналов с увеличением интервала mмежду отсчетами степень связи должна ослабевать в связи с уменьшением влияния инерционности реального процесса. При m=0 значения АКФ дают средний квадрат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.