Информатика и выч. техника \ Теория и обработка сигналов

Изучение основных характеристик стационарных случайных сигналов (среднего значения, автокорреляционной функции, спектральной плотности мощности), страница 2

Используя выражение связи между АКФ выходного и входного сигналов  линейной дискретной системы     ,  где  h[m]- импульсная характеристика, определим аналитически АКФ выходного сигнала для системы с уравнением:

при входном сигнале  в виде белого шума с АКФ  ,  при этом   - дисперсия (мощность) шума,   - единичный дельта-импульс.

Найдем импульсную характеристику системы:

Запишем выражение связи между АКФ выходного и входного сигналов ЛДС:

Вычислим свертку импульсных характеристик h[n] и h[-n]:

АКФ для выходного сигнала:

Найдем АКФ выходного сигнала,  используя процедуру conv() Matlab,  в качестве входа будем использовать случайный процесс X из п.1. Построим график .

n=-2:2;

h1=[5 2 -1];

h2=[-1 2 5];

y1=conv(h1,h2)

stem(y1)

>>

y1 =

    -5     8    30     8    -5

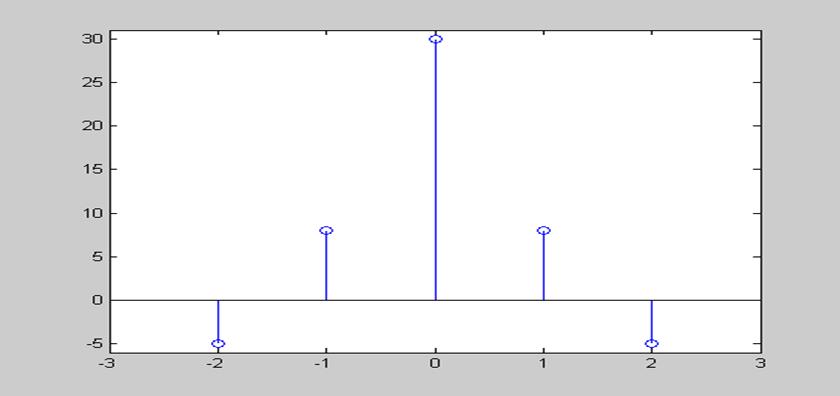
Рис. 3. График АКФ выходного сигнала.

4.Генерация случайного сигнала X  длительностью 1000 отсчетов, распределенного по нормальному закону с нулевым средним значением и единичной дисперсией. Вычисление выходного сигнала Y, используя уравнение системы по индивидуальному заданию. Построение на одной фигуре 4 графиков рассеяния с помощью функции plot(X, Y, ‘.’) для четырех случаев:
а)  (Yi, Yi+1),   б)  (Yi, Yi+2),  в)  (Yi, Yi+3),   г)  (Yi, Yi+4)   (i =1,2,…,900).

а)

X=randn(1,1000);

n=3:1000;

Y(n)=5*X(n)+2*X(n-1)-X(n-2);

i=1:900;

Y0(i)=Y(i);

Y1(i)=Y(i+1);

subplot(411)

plot(Y0,Y1,'.')

title('Graph of the diffusing Yi,Yi+1')

б)

Y2(i)=Y(i);

Y3(i)=Y(i+2);

subplot(412)

plot(Y2,Y3,'.')

title('Graph of the diffusing Yi,Yi+2')

в)

Y4(i)=Y(i);

Y5(i)=Y(i+3);

subplot(413)

plot(Y4,Y5,'.')

title('Graph of the diffusing Yi,Yi+3')

г)

Y6(i)=Y(i);

Y7(i)=Y(i+4);

subplot(414)

plot(Y6,Y7,'.')

title('Graph of the diffusing Yi,Yi+4')

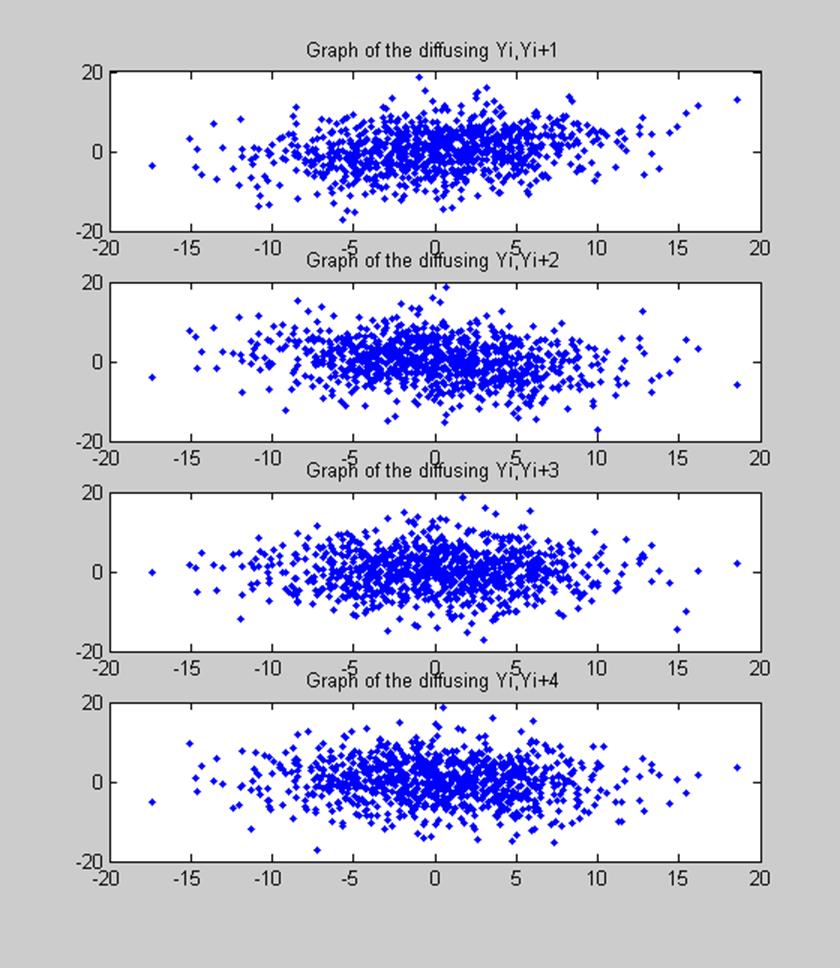
Рис. 4. Графики рассеяния для случаев

а)  (Yi, Yi+1),   б)  (Yi, Yi+2),  в)  (Yi, Yi+3),   г)  (Yi, Yi+4)

Выводы: при этом АКФ для СШС процессов не изменяется с изменением временного аргумента n, а зависит только от расстояния (сдвига) m. АКФ определяет,  как сильна связь между отсчетами сигнала, разделенными друг от друга интервалом m. Для реальных случайных сигналов с увеличением интервала m между отсчетами степень связи должна ослабевать в связи с уменьшением влияния инерционности  реального процесса. Поэтому и рассеяние на последнем графике наиболее заметное, так как степень связи между отсчетами сигнала наиболее слабая. 

На первом графике значения YiиYi+1 сильно коррелированны, поэтому, зная значение Yi ,можно предсказывать среднее значение  Yi+1 . Чем больше τ, тем меньше становится степень коррелированности значений, и, следовательно, прогнозировать значения Yi+τ становится гораздо сложнее.

5.Определение оценки автокорреляционной функции выходного сигнала при входном  сигнале из п. 1., используя функцию xcorr()  с параметром ‘biased’ (смещенная оценка). Построение на одной фигуре графиков АКФ, полученных  в п. 2 и в п. 5. С помощью этой же функции определение и построение графиков взаимной корреляционной функции выходного и входного сигналов фильтра.

X=randn(1,500);

h=[25 20 -6 -4 1];

x=xcorr(X,'biased');

y=conv(h,x);

subplot(2,1,1)

plot(y)

title('Correlation function')

axis([0,1000,-10,50])

f=xcorr(X,'biased');

subplot(2,1,2)

plot(f)

axis([0,1000,-0.5,1.5])

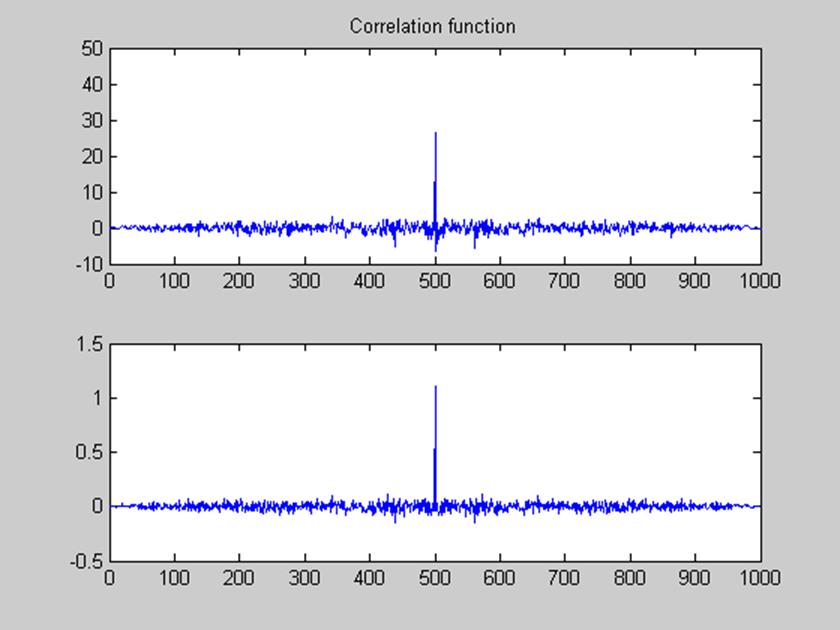
Рис. 5. Графики АКФ выходного сигнала из пункта 3 и пункта 5 соответственно.

X=randn(1,500);

num=[0.8 1 0.4];

den=[1];

f=filter(num,den,X);

z=xcorr(f,X);

plot(z)

title('ВКФ выходного и входного cигнала для системы')

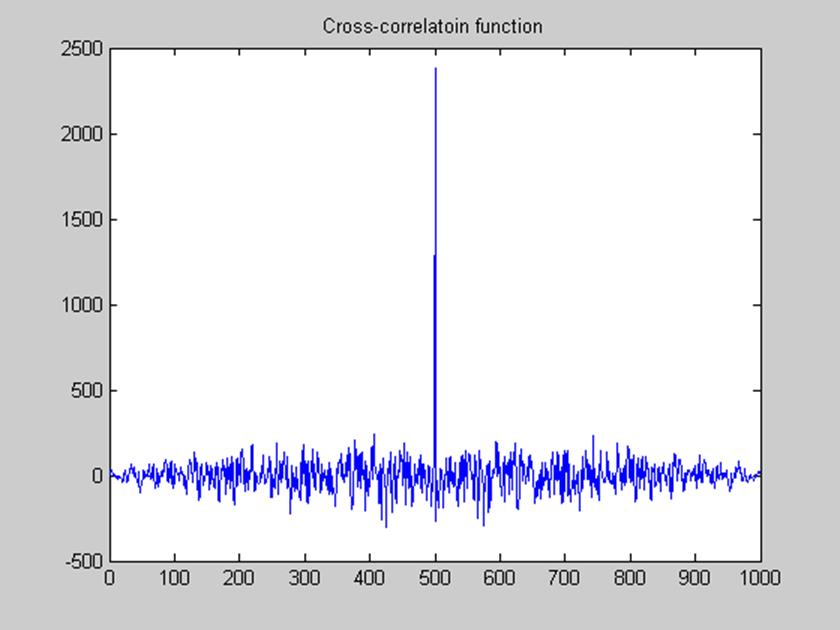
Рис. 6. Взаимная корреляционная функция входного и выходного сигналов.

Если АКФ показывает степень сходства между сдвинутыми копиями одного и того же сигнала, то взаимная корреляционная функция позволяет определить аналогичную величину для сдвинутых экземпляров двух разных сигналов, являясь, таким образом, характеристикой связи двух случайных сигналов.

ВКФ определяется выражением:

6. Генерация случайного гауссовского сигнала с  нулевым средним значением и дисперсией, равной 1, длительностью 1000 отсчетов.  Определение частотой характеристики фильтра. Гауссовский сигнал рассматривается как входной сигнал фильтра. Построение на одной фигуре графиков АЧХ фильтра, спектральной плотности мощности входного и выходного сигналов.

>> sig=random('norm',0,1,1,1000);

>> plot(sig)

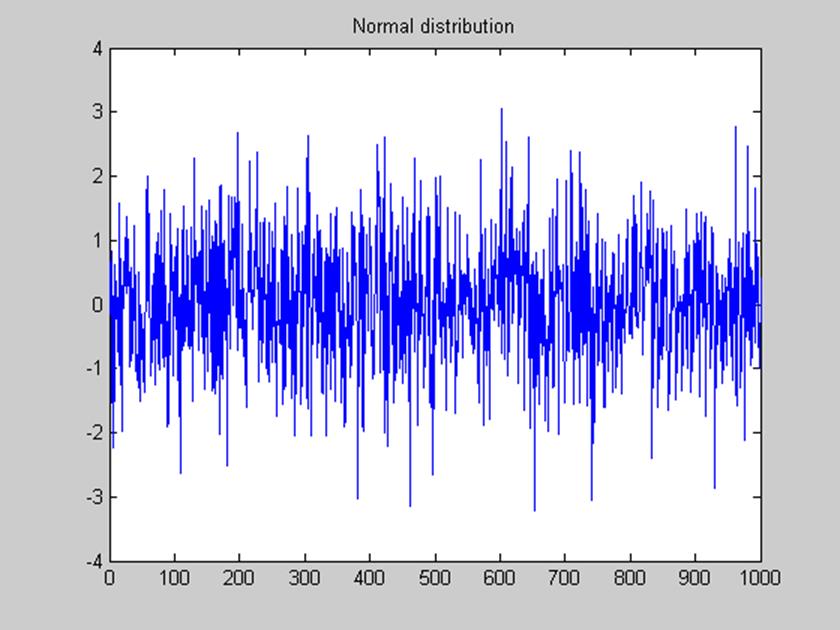
Рис. 7. Гауссовский случайный сигнал с  нулевым средним значением и

дисперсией, равной 1, длительностью 1000 отсчетов.

Определение частотной характеристики фильтра:


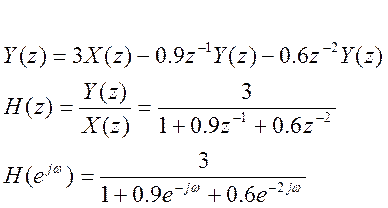
% Формирование частотной шкалы

% и построение частотной характеристики фильтра

Ts=0.01; T=10;  % интервал отсчетов и длительность сигнала

df=1/T; Fmax=1/Ts;

f=0:df:Fmax/2;  % частотная шкала

d1=length(f);

% Частотная характеристика фильтра

H=2./(1+0.9*exp(-j*2*pi*f*Ts)+0.6*exp(-j*4*pi*f*Ts));

X=randn(1,500);

num=[3 -0.9 -0.6];

den=[1];

figure(1)

subplot(3,1,1), plot(f,abs(H))

title('Magnitude response')

% Вычисление и построение спектра мощности входного шума

t=0:Ts:T;

X=random('norm',0,1,1,1000);  % Генерирование входного шума

[Sxx, f1]=psd(X,d1, Fmax); % Вычисление спектра мощности входа

subplot(3,1,2), stem(f1,Sxx), axis([0,50,0,30])

title('Spectrum to powers of the input signal')

% Вычисление и построение спектра мощности выхода

i=3:length(X);

Y=zeros(1, length(X));

% Формирование выходного сигнала фильтра

num=[3];

den=[1 0.9 0.6];

Y=filter(num,den,X);

 [Syy, f2]=psd(Y,d1,Fmax); % Спектр мощности выхода

subplot(3,1,3), stem(f2,Syy), axis([0,50,0,1100])

title('Spectrum to powers of the output signal')

xlabel(' Frequency,  Hz')

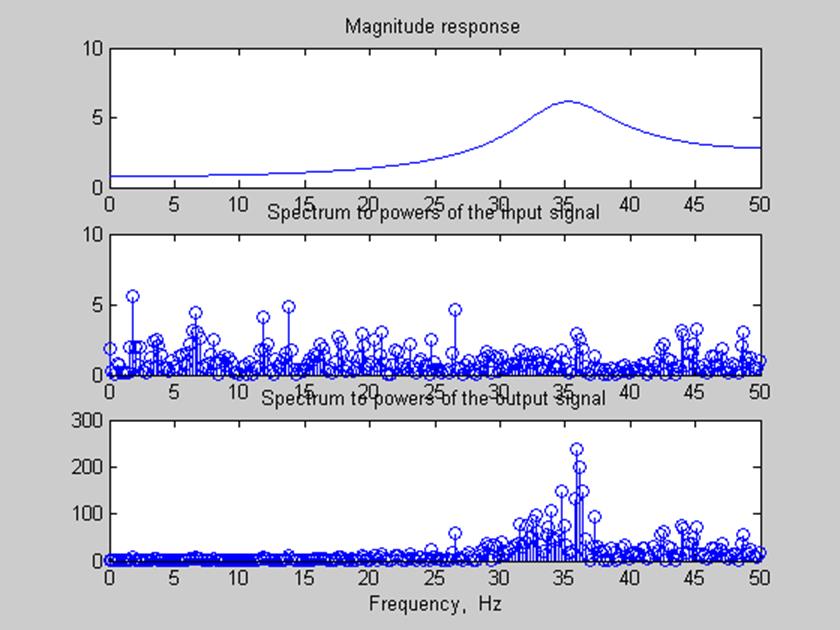
Рис. 8. АЧХ фильтра, спектр мощности входящего сигнала, спектр

 мощности сигнала на выходе фильтра.

Вывод:

          Мощность выходного сигнала в полосе пропускания зависит от коэффициента передачи фильтра. Мощность пропорциональна квадрату коэффициента передачи фильтра. Если уменьшить коэффициент передачи, то естественно, что, мощность выходного сигнала станет меньше, что и видно из представленных графиков.

          Из графика видно, что после прохождения через фильтр мощность сигнала в полосе задерживания уменьшилась, а в полосе пропускания увеличилась.

Скачать файл