Изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем. Вариант 7

            МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

ЛАБОРАТОРНАЯ  РАБОТА  № 10

ЛИНЕЙНЫЕ ДИСКРЕТНЫЕ СИСТЕМЫ

Вариант 7

Группа: АТ-73                                                                             Преподаватель: доц. Щетинин Ю.И.

Студент: Кухарева А.В.

Новосибирск

 2010

Цель работы: изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем и приобретение практических навыков  их анализа в среде Matlab.

1.  Дискретизация аналогового фильтра.

ФВЧ
    

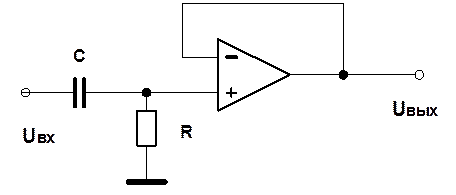
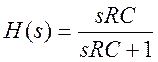
C=0,5 мкФ,   R=1 кОм                                                                       

Дана схема аналогового ФВЧ (рис.1).

									Y2
					Y4

Рис. 1. Схема аналогового ФВЧ.

В предположении идеального операционного усилителя передаточная функция фильтра имеет вид

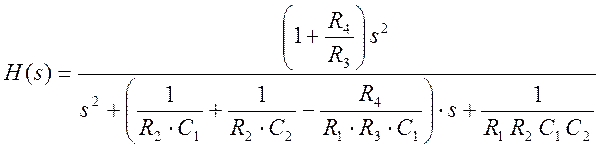                                                      (1)

Обозначим ,     ,       .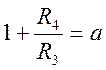

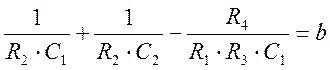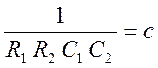Получим

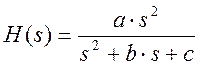                                                                                                                (2)

Запишем  по виду передаточной функции дифференциальное уравнение, связывающее выходное и входное напряжения фильтра

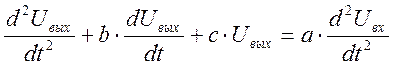                                                                                         (3)

Произведем дискретизацию аналогового фильтра с интервалом отсчетов Δt.

Для этого заменим в выражении (3) производную конечной разностью вида

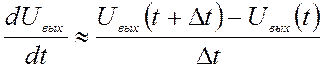,                                                                                                       (4)

где   - величина шага приращения времени (интервал дискретизации).

Формула для производной второго порядка через конечные разности

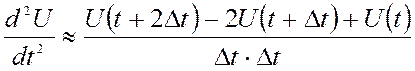                                                                                        (5)

При этом уравнение (3) преобразовывается к виду

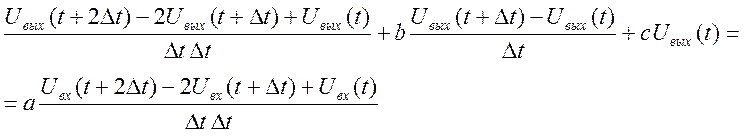                                  (6)

Положим    и обозначим  , аналогично . 

Тогда выражение (6) приобретает вид

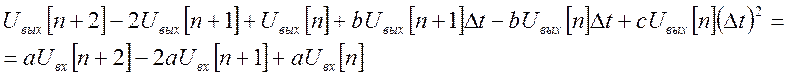                         (7)

Далее при исследовании заданного фильтра будем использовать следующие значения сопротивлений и емкостей:

С1=2 мкФ, С2=5 мкФ,  R1=1 кОм, R2=0.5 кОм, R3=5 кОм,  R4=0.5 кОм.

При данных значениях рассматриваемый фильтр является фильтром верхних частот с частотой среза f_c по уровню 3 дБ, равной 192 Гц (рис. 2).

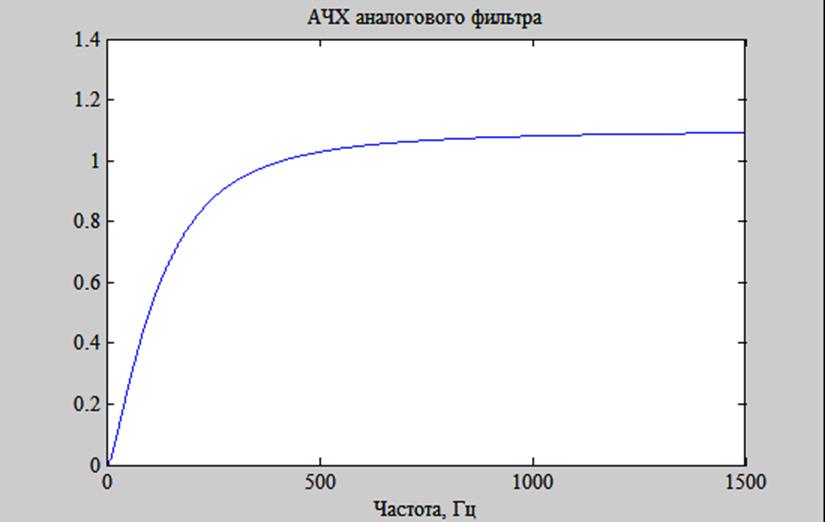
Рис. 2. АЧХ аналогового ФВЧ.

Верхняя граничная частота дискретного фильтра равна половине частоты отсчетов F_s.  Выберем для данного случая значение F_s = 10 ⁴ Гц, что соответствует интервалу (периоду) отсчетов     

Подставив в выражение (7) выбранные значения , сопротивлений и емкостей и преобразовав результат, получим разностное уравнение (8).

                (8)

2.  Определение передаточной функции системы, разложение её на простые дроби и определение импульсной характеристики аналитически.

Для получения передаточной функции системы возьмем  Z - преобразование от левой и правой части уравнения (8).

С учетом теоремы сдвига получим

                   (9)

Запишем передаточную функцию дискретного фильтра как отношение Z - преобразований выходного и входного сигналов

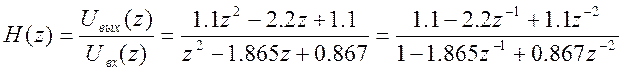                                                (10)

Разложим полученную передаточную функцию на простые дроби.

Воспользуемся следующей последовательностью команд для определения полюсов, вычетов и коэффициентов целой части.

num = [1.1    -2.2     1.1];

den = [1      –1.865   0.867];

[r, p, k]=residuez(num,den)

Получим

r =

    0.0032

   -0.1719

p =

    0.9831

    0.8819

k = 1.2687

Запишем разложение передаточной функции на простые дроби 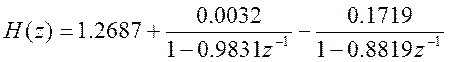(11).

                                                                             (11)

Используя полученное разложение, найдём аналитически импульсную характеристику системы как обратное Z – преобразование от передаточной функции.

Так как   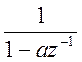,      то   ,

 .

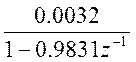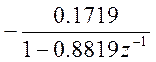Так как , то  .

Таким образом, получили импульсную характеристику системы (12).

                                                            (12)

С помощью следующей последовательности команд построим график импульсной характеристики по выражению (12).

n = 1: 100;

n1 = 0: 100;

h = [1.2687+0.0032-0.1719 0.0032*(0.9831).^n-0.1719*(0.8819).^n];

stem(n1, h)

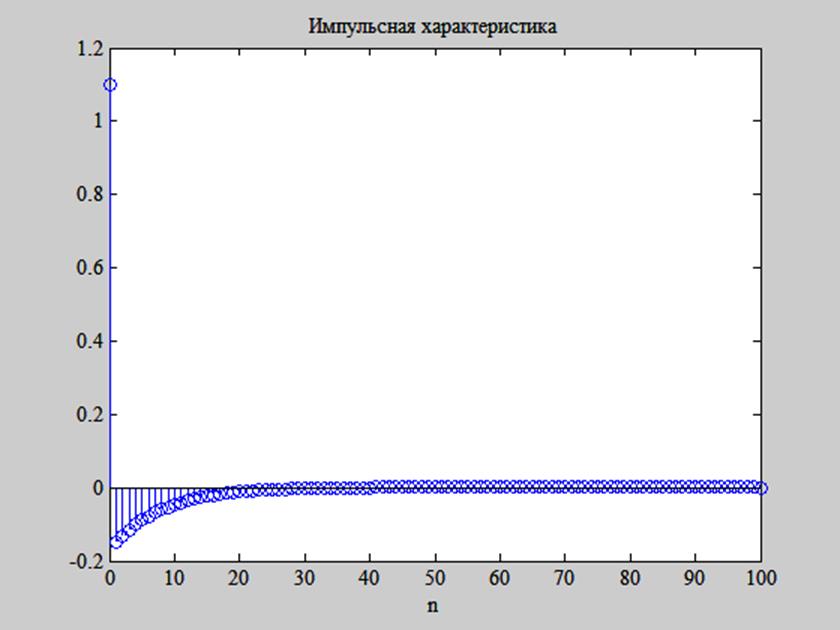
Рис. 3. График импульсной характеристики, определённой аналитически.

На рис. 3 видим, что график импульсной характеристики системы стремится к нулю, значит система устойчива и для ограниченного входного сигнала на выходе получим ограниченный выходной.

3.  Построение диаграммы нулей и полюсов системы.

С помощью следующей последовательности команд определим полюса и нули системы как корни знаменателя и числителя передаточной функции, а также построим диаграмму нулей и полюсов.

num = [1.1    -2.2     1.1];

den = [1      -1.865   0.867];

Z = roots(num)

P = roots(den)

zplane(Z, P)

Получили следующие значения нулей и полюсов

Z =

        1

        1

P =

       0.9831

       0.8819

Полученная диаграмма нулей и полюсов изображена на рис. 4.

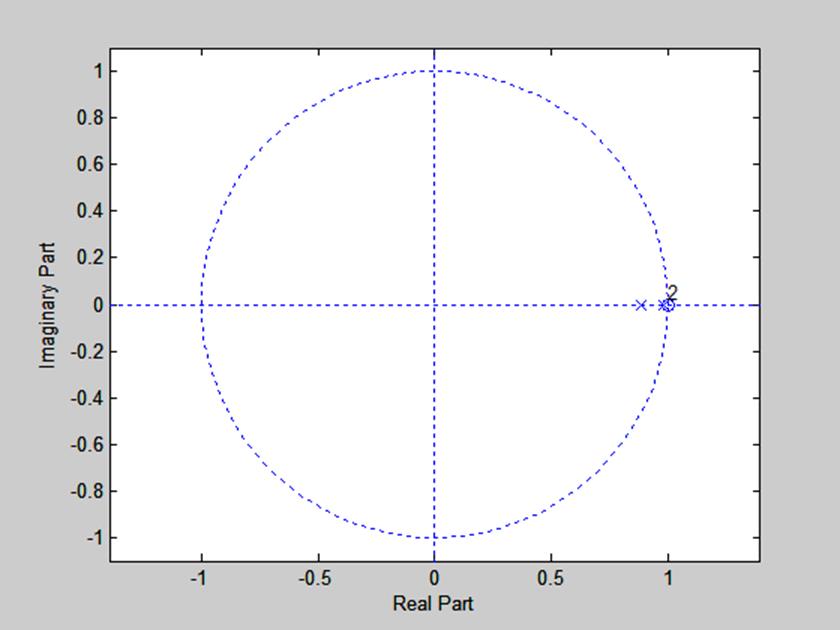
Рис. 4. Диаграмма нулей и полюсов системы.

На диаграмме рис. 4 видим, что нули и полюса лежат внутри единичной окружности, значит, система устойчива. Данный результат соответствует виду импульсной характеристики системы, приведённому на рис. 3.

Зная значения полюсов и нулей системы, запишем полюсно-нулевое представление передаточной функции.

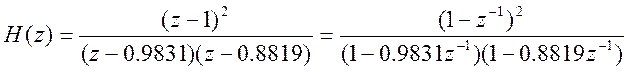                                               (13)

Преобразовав выражение (13), получим

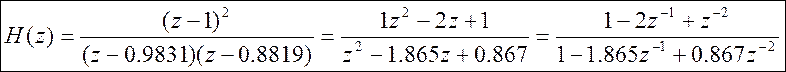                               (14)

Видим, что выражение (14) совпадает с выражением ПФ системы (10) с точностью до константы усиления k = 1.1. Значит, передаточная функция системы с точностью до константы определяется расположением нулей и полюсов в z- плоскости.

4.  Определение частотной характеристики системы с помощью функции freqz().

С помощью следующей последовательности команд проведём расчет частотной характеристики системы и построим графики её АЧХ и ФЧХ, используя функцию freqz().

num = [1.1    -2.2     1.1];

den = [1      –1.865   0.867];

subplot(2,1,1);

[H,F] = FREQZ(num,den,100000,10^4);

plot(F, abs(H))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('АЧХ цифрового фильтра');

subplot(2,1,2);

plot(F, angle(H))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('ФЧХ цифрового фильтра');

xlabel('Частота, Гц');

Результат представлен на рис. 5.

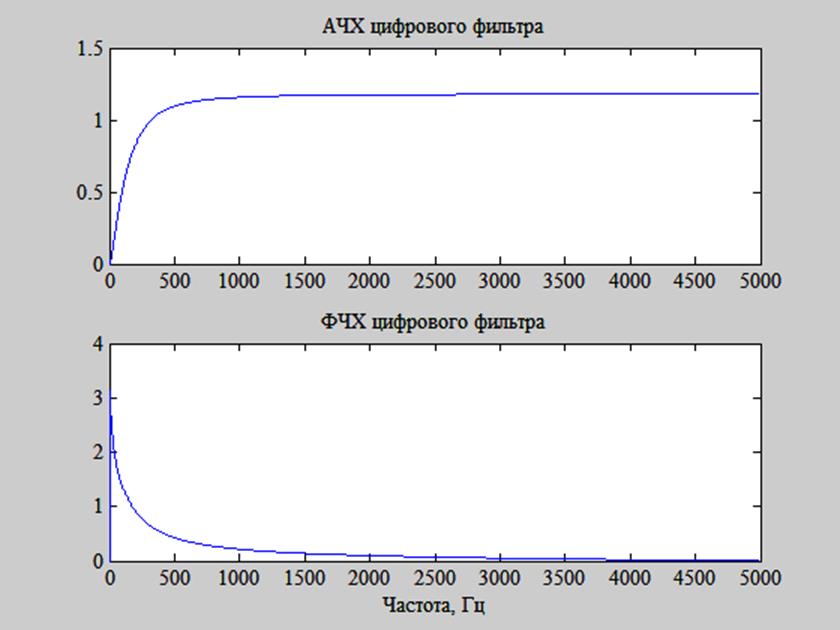
Рис. 5. Графики АЧХ и ФЧХ рассматриваемой системы.

На рис. 5 видим, что данная система является фильтром верхних частот.

Частота среза f_c данного фильтра по уровню 3 дБ, равна 180 Гц.

Для сравнения построим графики АЧХ и ФЧХ аналогового и цифрового фильтров в одной системе координат.

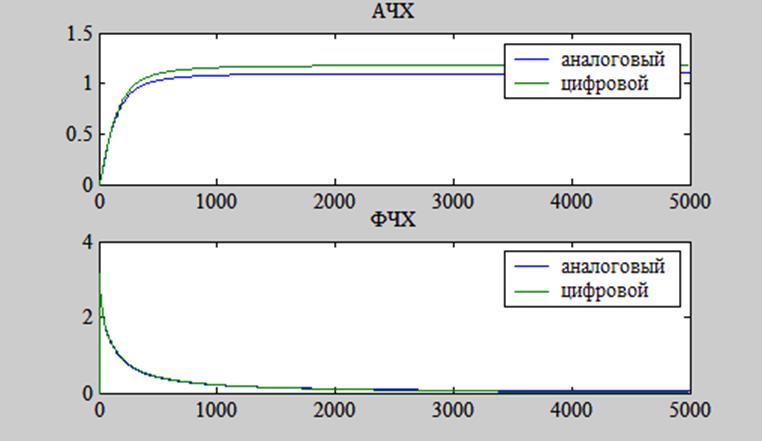
Рис. 6. Графики АЧХ и ФЧХ аналогового и цифрового фильтров.

На рис. 6 видим, что расхождение между графиками АЧХ аналогового и цифрового фильтров равно приблизительно 0.1, а между их ФЧХ расхождений не наблюдается.

Частота среза аналогового фильтра равна 192 Гц, а дискретного – 180 Гц.