Информатика и выч. техника \ Теория и обработка сигналов

Изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем. Вариант 7, страница 2

5.  Фильтрация суммы гармоник с помощью функции filter().

С помощью следующей последовательности команд сгенерируем сигнал, равный сумме гармоник с частотами 50 Гц и 2000 Гц, и осуществим фильтрацию данного сигнала с помощью функции filter().

num = [1.1    -2.2     1.1];

den = [1      –1.865   0.867];

n = 0: 0.00001: 0.04;

x = cos(2*pi*2000*n) + cos(2*pi*50*n);

y = filter(num, den, x);

subplot(2,1,1);

plot(n, x);

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Исходная сумма гармоник');

subplot(2,1,2);

plot(n, y);

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Отфильтрованный сигнал');

Полученный результат представлен на рис. 6.

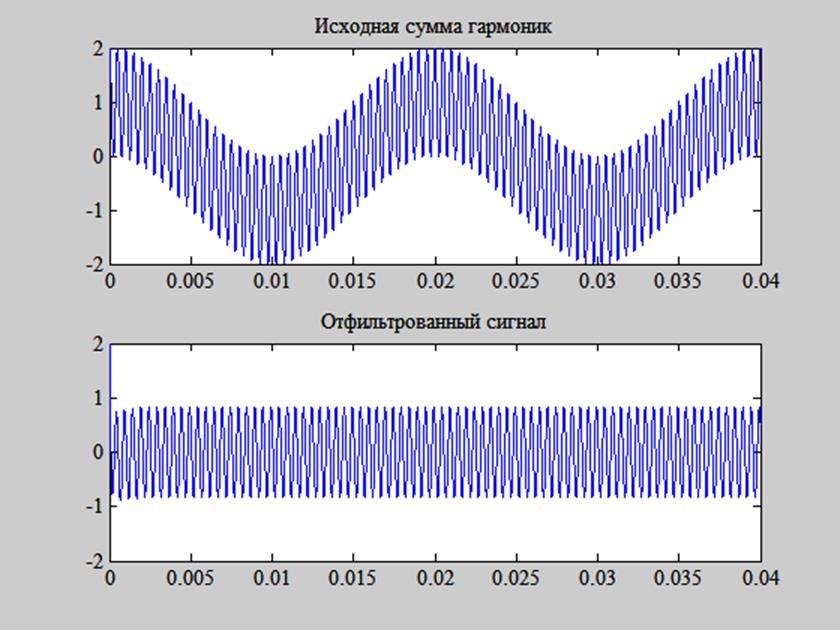
Рис. 6. Графики исходного и отфильтрованного сигналов.

На рис. 6 видим, что сигнал частотой 50 Гц, присутствовавший в исходной сумме, был подавлен в результате фильтрации, а сигнал 2000 Гц остался практически неизменным.

Данный результат соответствует ожидаемому, т.к. по виду АЧХ фильтра (рис. 5) видно, что частота 50 Гц находится в полосе задерживания фильтра, а частота 2000 Гц – в полосе пропускания.

Аналогичный результат можно получить, заменив функцию filter() на функцию dlsim() с синтаксисом:

y = dlsim(num, den, x);

6.  Исследование влияния расположения нулей и полюсов на частотную характеристику системы.

Для исследования влияния расположения нулей и полюсов на частотную характеристику системы выберем два новых набора нулей и полюсов и построим АЧХ системы для этих наборов.

1)  Нули: , .       Полюса: , .

С помощью следующей последовательности команд зададим значения нулей и полюсов и построим диаграмму.

Z = [1;  0.4];

P = [0.5;    0.3];

K = 1;

figure(1)

zplane(Z, P)

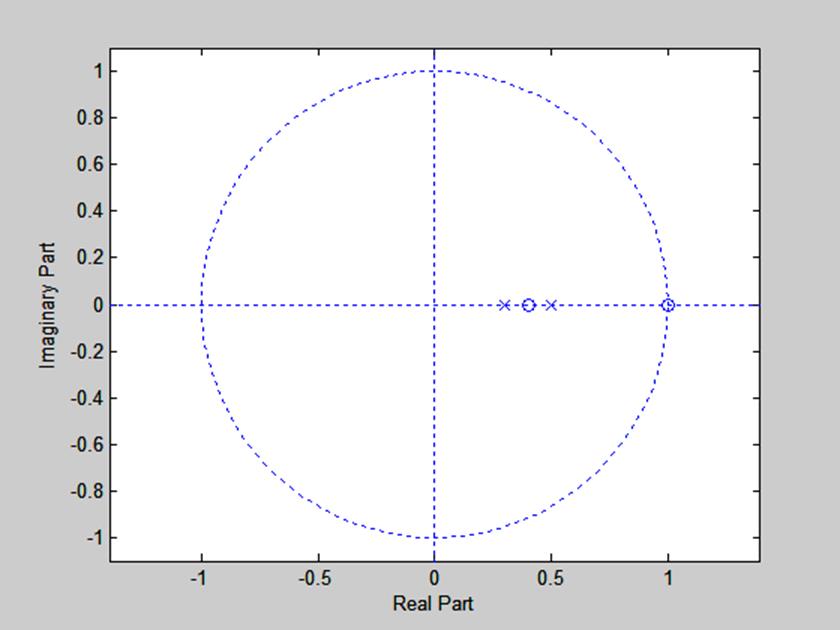
Рис. 7. Диаграмма нулей и полюсов.

Для полюсно-нулевого представления частотной характеристики системы можно записать выражение АЧХ в виде 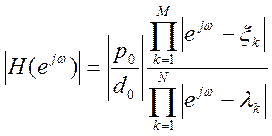(15).

                                                                                                           (15)

Каждый член в числителе и знаменателе выражения  (15) имеет вид , где - нуль или полюс.

В  z - плоскости  разность  представляет собой вектор, начинающийся в точке и заканчивающийся на единичной окружности в точке  для определенной  частоты ω. При изменении ω изменяется длина векторов , значит, изменяется значение АЧХ на данной частоте и это значение можно вычислить, зная расположение нулей и полюсов системы.

Вычислим значения АЧХ при некоторых значениях частоты.

,                                                   

,                              

,                              

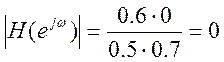
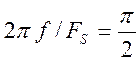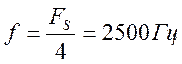
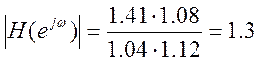
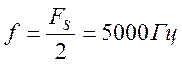
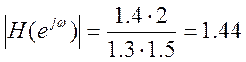
Построим эскиз АЧХ.

 


Рис. 8. Эскиз АЧХ системы.

С помощью следующей последовательности команд преобразуем полюсно-нулевое представление системы в передаточную функцию и построим график АЧХ системы.

[num,den] = ZP2TF(Z,P,K)

figure(2)

[H,F] = FREQZ(num,den,100000,10^4);

plot(F, abs(H))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('АЧХ цифрового фильтра');

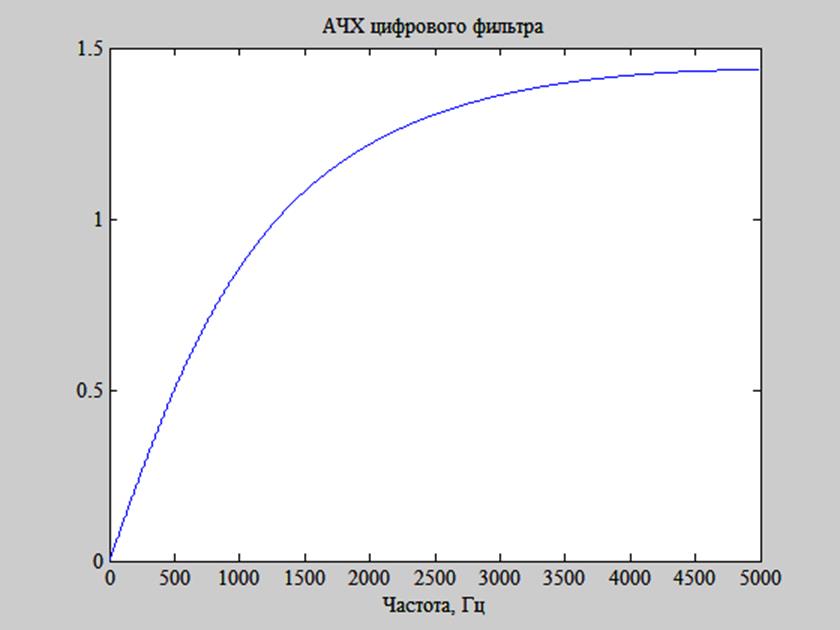
Рис. 9. АЧХ системы.

Сравнив АЧХ системы (рис. 9) с эскизом АЧХ (рис. 8) видим, что они имеют схожий вид и в точках, где значение АЧХ было вычислено исходя из расположения полюсов и нулей, эти значения совпадают с истинными. Значит, АЧХ системы можно построить, зная расположение её нулей и полюсов.

2)  Нули: , .       Полюса: , .

С помощью следующей последовательности команд зададим значения нулей и полюсов и построим диаграмму.

Z = [0.4 + 0.7*j;    0.4 - 0.7*j];

P = [0.9;  0.4];

K = 1;

figure(1)

zplane(Z, P)

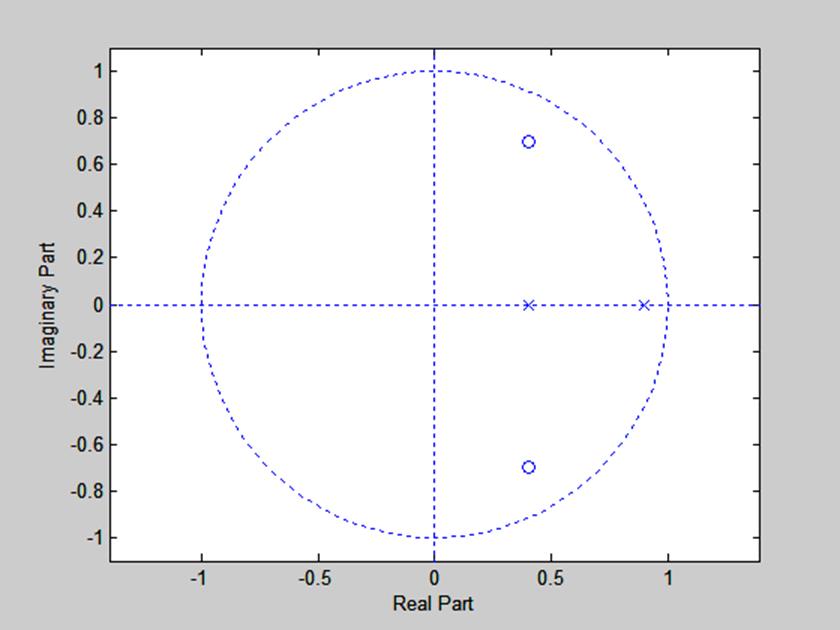
Рис. 10. Диаграмма нулей и полюсов.

Вычислим значения АЧХ при некоторых значениях частоты.

,                                                   

,                              

,                              

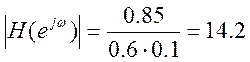
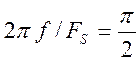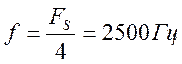
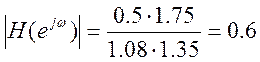
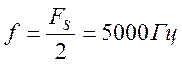
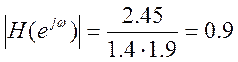
Построим эскиз АЧХ.

 


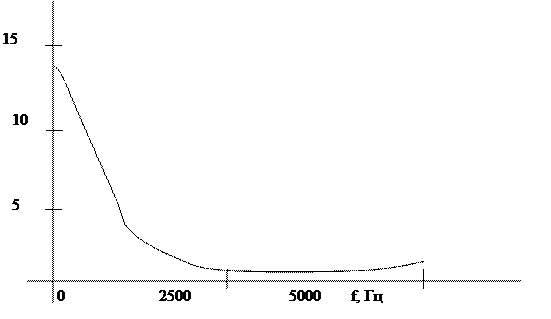Рис. 11. Эскиз АЧХ системы.

С помощью следующей последовательности команд преобразуем полюсно-нулевое представление системы в передаточную функцию и построим график АЧХ системы.

[num,den] = ZP2TF(Z,P,K)

figure(2)

[H,F] = FREQZ(num,den,100000,10^4);

plot(F, abs(H))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('АЧХ цифрового фильтра');

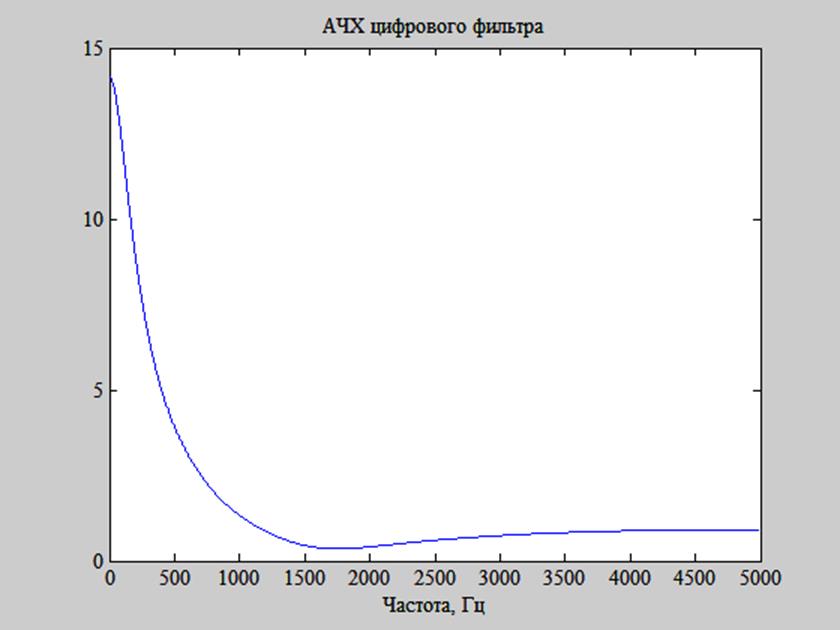
Рис. 12. АЧХ системы.

Сравнив АЧХ системы (рис. 12) с эскизом АЧХ (рис. 11) видим, что они имеют схожий вид и в точках, где значение АЧХ было вычислено исходя из расположения полюсов и нулей, эти значения совпадают с истинными. Значит, АЧХ системы можно построить, зная расположение её нулей и полюсов.

7.  Определение импульсной характеристики системы с помощью функций impz() и dimpulse().

C помощью следующей последовательности команд построим графики импульсной характеристики системы, используя функции impz() и dimpulse().

num = [1.1    -2.2     1.1];

den = [1      –1.865   0.867];

figure(1)

[H,T] = IMPZ(num,den, 100);

stem(T, H)

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Импульсная характеристика');

xlabel('n');

figure(2)

dimpulse(num, den, 100)

Полученные результаты  представлены на рис. 13 и 14.

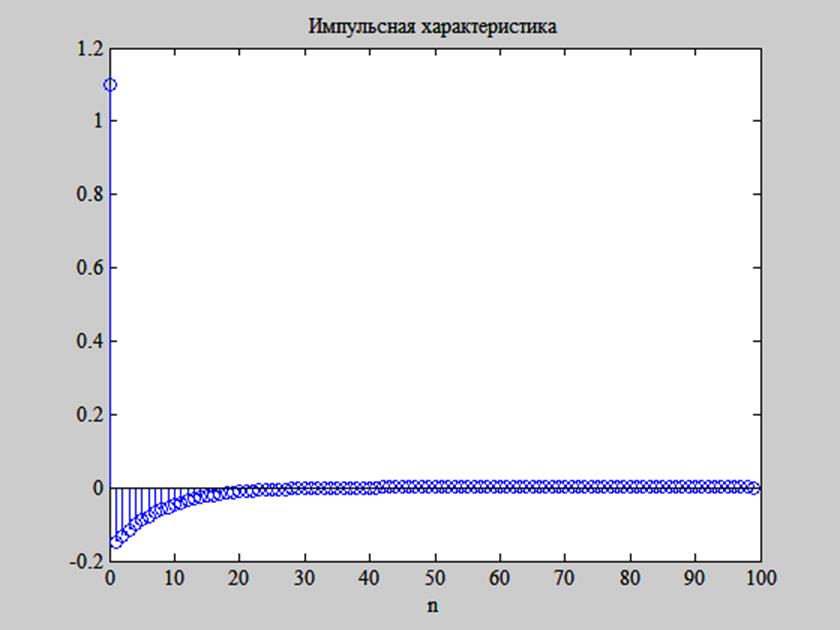
Рис. 13. Импульсная характеристика системы, найденная с помощью impz().

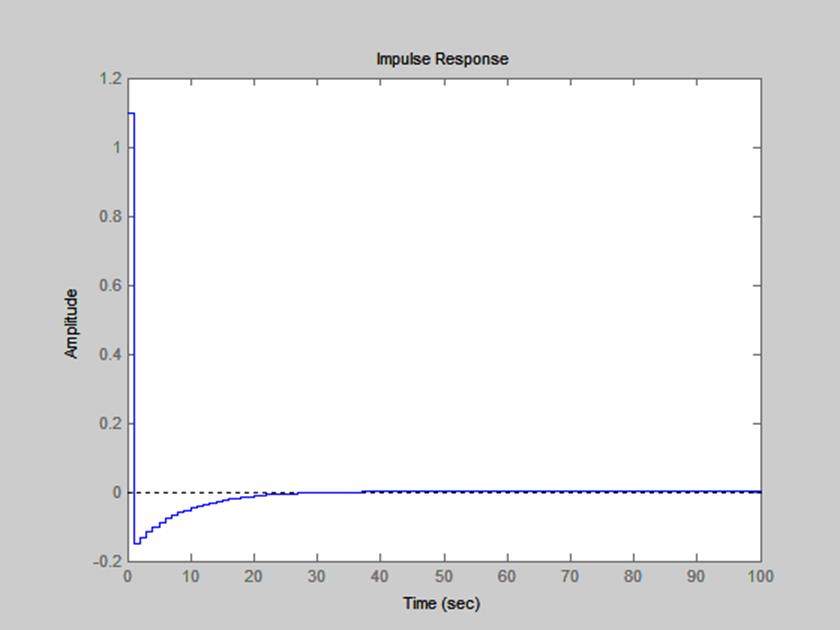
Рис. 14. Импульсная характеристика системы, найденная с помощью dimpulse().

Сравнив графики, изображённые на рис. 13 и 14, с графиком импульсной характеристики, определённой аналитически как обратное Z – преобразование от передаточной функции системы (рис. 3), видим, что все три графика практически одинаковы.

8.  Построение графика переходной характеристики фильтра с помощью функции dstep().

C помощью следующей последовательности команд построим график переходной характеристики системы, воспользовавшись функцией dstep().

num = [1.1    -2.2     1.1];

den = [1      –1.865   0.867];

dstep(num, den, 100)

Полученный результат представлен на рис. 15.

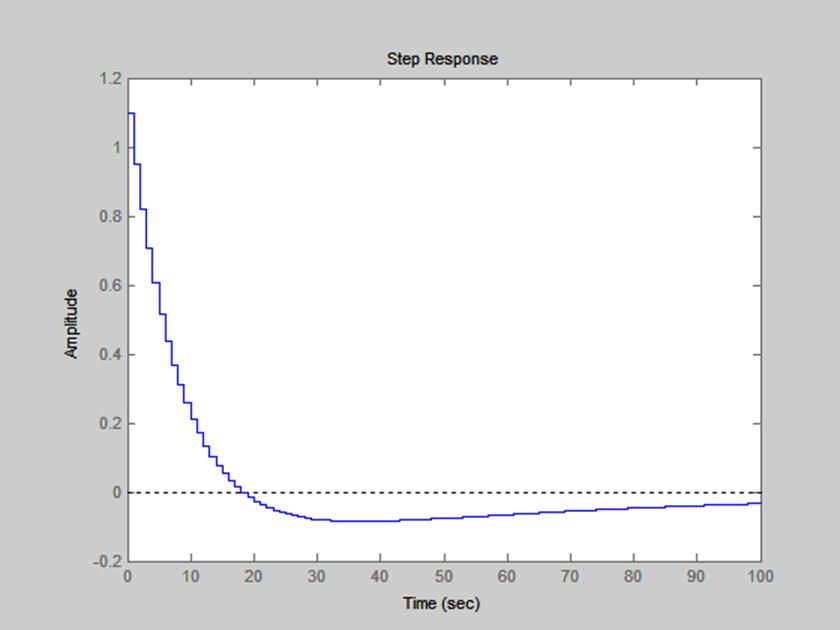
Рис. 15. Переходная характеристика системы, найденная с помощью dstep().

Выводы:

1.  Дискретные линейные стационарные системы описываются линейными разностными уравнениями с постоянными коэффициентами.

Разностное уравнение, описывающее дискретную систему можно получить из дифференциального уравнения, задающего аналоговую систему, с помощью процедуры дискретизации. Такая процедура была проведена в п.1.

2.  Характеристикой систем в области переменной z является передаточная функция, которая определяется как отношение Z - преобразований выходного и входного сигналов.

3.  Импульсной характеристикой системы является выходной сигнал системы при подаче на её вход функции . Также импульсную характеристику можно получить как обратное Z – преобразование передаточной функции системы (п.2).

В Matlab для определения импульсной характеристики используются функции impz() и dimpulse(). В п.7 было показано, что определение импульсной характеристики с помощью этих функций и аналитически даёт одинаковые результаты.

4.  В п.3 было показано, что передаточная функция системы с точностью до константы определяется расположением нулей и полюсов в z- плоскости.

5.  Изменение амплитуды гармоники при прохождении через систему характеризуется АЧХ, а фазы – ФЧХ. Для расчёта ЧХ дискретных систем в Matlab используется функция freqz().  

6.  Для действительной гармоники   выходной сигнал. В п.5 данное утверждение было проиллюстрировано: гармоника с частотой из полосы задерживания не попала в выходной сигнал, т.к. значение АЧХ на данной частоте мало.

Скачать файл