
ЦИФРОВЫЕ ФИЛЬТРЫ
С КОНЕЧНОЙ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКОЙ
Группа: АО-21
Студентка: Перевалова В.А.
Цель работы:изучение методов анализа и синтеза фильтров с конечной импульсной характеристикой с использованием сглаживающих оконных функций
ЗАДАНИЕ № 2
Постройте в одном графическом окне графики импульсной характеристики КИХ-фильтра нижних частот с прямоугольным окном частотой среза
![]() для
двух значений длины фильтра N = 15 и N = 50.
для
двух значений длины фильтра N = 15 и N = 50.
Для того, чтобы ограничить бесконечную импульсную характеристику соответствующим размером окна необходимо сначала сдвинуть ее на (N-1)/2 отсчетов, где N размер окна, а затем умножить на функцию окна.
М-файл для построения импульсной характеристики КИХ-фильтра:
n=-60:0.3:60; %временной интервал
w=2; %частота среза
N1=15; %длина фильтра
N2=50;
h1=sin(w*(n-(N1-1)/2))./(pi.*(n-(N1-1)/2));%импульсная
%характеристика
h2=sin(w*(n-(N2-1)/2))./(pi.*(n-(N2-1)/2));
W1=rectpuls(n-(N1-1)/2,N1); % прямоугольное окно
W2=rectpuls(n-(N2-1)/2,N2);
hog1=h1.*W1; % ИХ, ограниченная прямоугольным окном размером N=15
hog2=h2.*W2; % ИХ, ограниченная прямоугольным окном размером N=50
figure
subplot(211); plot(n,hog1)
title('Импульсная характеристика для N=15')
axis([-2,18,-0.2,0.8]);
subplot(212); plot(n,hog2)
title('Импульсная характеристика для N=50')
axis([-3,60,-0.2,0.8]);
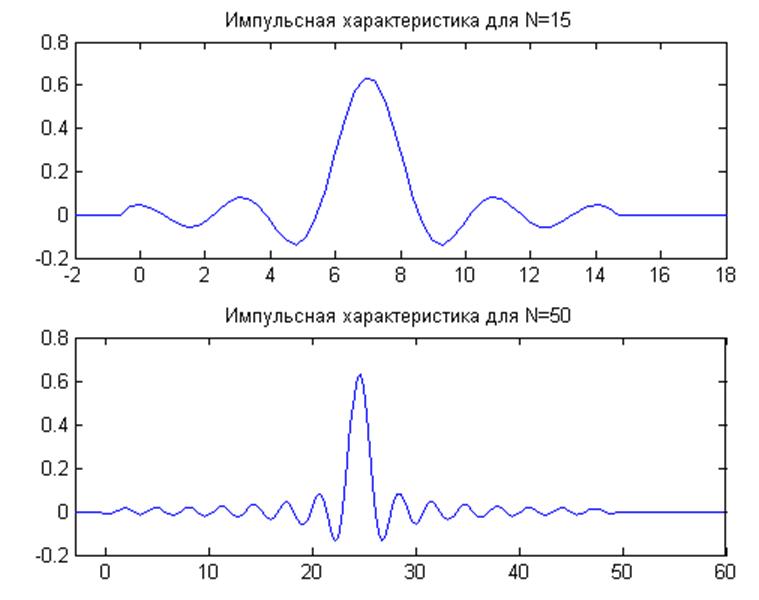
Рис.1
На графике представлена импульсная характеристика КИХ-фильтра, ограниченная размером окна, т.е. на графике явно видно, что за пределами окна импульсная характеристика принимает нулевое значение. Из графика видно, что с увеличением N длина импульсной характеристики увеличивается, но пульсации становятся более узкими.
ЗАДАНИЕ № 3
Используя функцию DTFT (Приложение 4), вычислите ДВПФ импульсных характеристик из п.2 и постройте графики их АЧХ в линейном масштабе (одно графическое окно) и в децибелах (20*log10(H(ejω) – другое окно) для 512 отсчетов частоты. По характеристикам в линейном масштабе определите полосу пропускания, переходную полосу и полосу задерживания фильтра.
Функция DTFT:
function [X,w] = DTFT(x,M)
N = max(M,length(x));
N = 2^(ceil(log(N)/log(2)));
X = fft(x,N);
w = 2*pi*( (0:(N-1))/N );
w = w - 2*pi*(w>=pi);
X = fftshift(X);
w = fftshift(w);
М-файл для вычисления ДВПФ импульсных характеристик:
[H1,w1]=DTFT(hog1,512); %вычисление ДВПФ ИХ
[H2,w2]=DTFT(hog2,512);
figure
subplot(211); plot(w1,abs(H1/max(H1)));%построение АЧХ в
title('АЧХ в линейном масштабе')
subplot(212); plot(w2,abs(H2/max(H2))); %линейном масштабе
figure
subplot(211); plot(w1,20*log10(H1)); %построение АЧХ в
title('АЧХ в логарафмическом масштабе')
subplot(212); plot(w2,20*log10(H2)); %логарифмическом масштабе
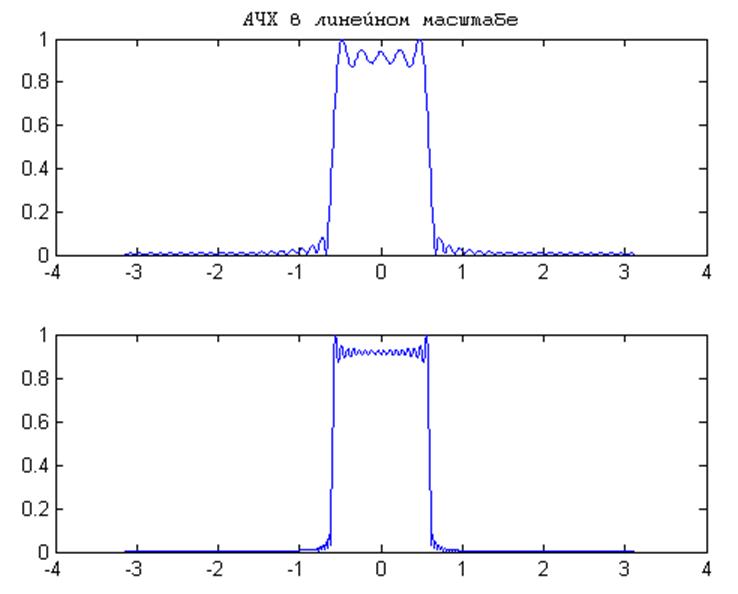
Рис.2
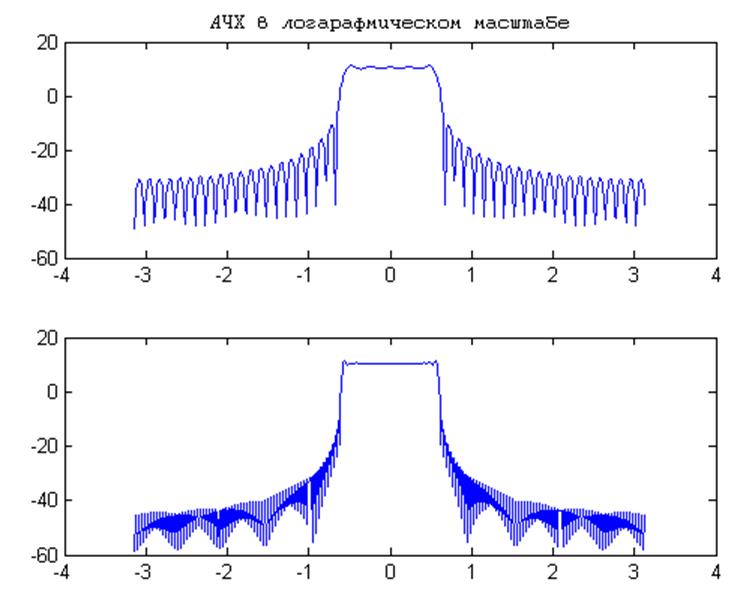
Рис.3
В результате усечения и сдвига ИХ у реального фильтра по сравнению с идеальным появились переходная область и пульсации в полосе пропускания и задерживания, которые возникают вследствие явления Гиббса. С увеличением N, тем пульсаций становятся более узкими.
Ширина переходной полосы фильтра определяется шириной главного лепестка, которая уменьшается с увеличением N. Пульсации определяются площадями боковых лепестков, которые не меняются при изменении N.
ЗАДАНЕИ № 4
С помощью функции load() загрузите в рабочее пространство Matlab файл speech.mat. Используя операцию свертки, выполните фильтрацию сигнала speech каждым из двух фильтров.
>> load speech.mat
>> sound(nspeech2)
>>S1=conv(nspeech2,FO1);
>>sound(S1)
>>S2=conv(nspeech2,FO2);
>>sound(S2)
Перед фильтрацией в прослушиваемом звуке достаточно хорошо слышны помехи (шум). После фильтрации первым фильтром звук становится более чище, т.е. помехи практически отсутствуют . После фильтрации вторым фильтром слышен уже чистый звук, помехи отсутствуют. Это можно объяснить тем, что у второго фильтра переходная полоса уже, чем у первого, поэтому он не пропускает помехи, что можно увидеть из приведенного ниже Рис.4.
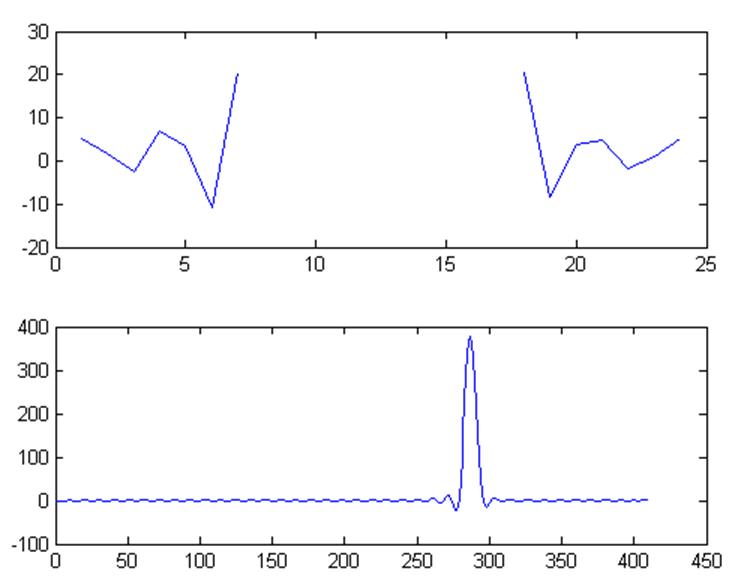
Рис.4
ЗАДАНИЕ № 5
Постройте в одном графическом окне графики прямоугольного окна и окон Хэмминга, Ханна, Блэкмана для N = 25. Используйте для этого команды Matlab hamming, hanning, blackman.
n=-12:12;% временной интервал
n1=-13:0.1:13;
N=25;%длина окна
Wp=rectpuls(n1,N);%прямоугольное окно
Whm=hamming(N);% окно Хемминга
Whn=hanning(N);%окно Ханна
Wb=blackman(N);%окно Блэкмана
subplot(411); plot(n1,Wp);
title('Прямоугольное окно')
subplot(412); plot(n,Whm,'r');
title('окно Хемминга')
subplot(413); plot(n,Whn,'-k');
title('окно Ханна')
subplot(414); plot(n,Wb,'g');
title('окно Блекмана')
axis([-15,15,0,1.2]);
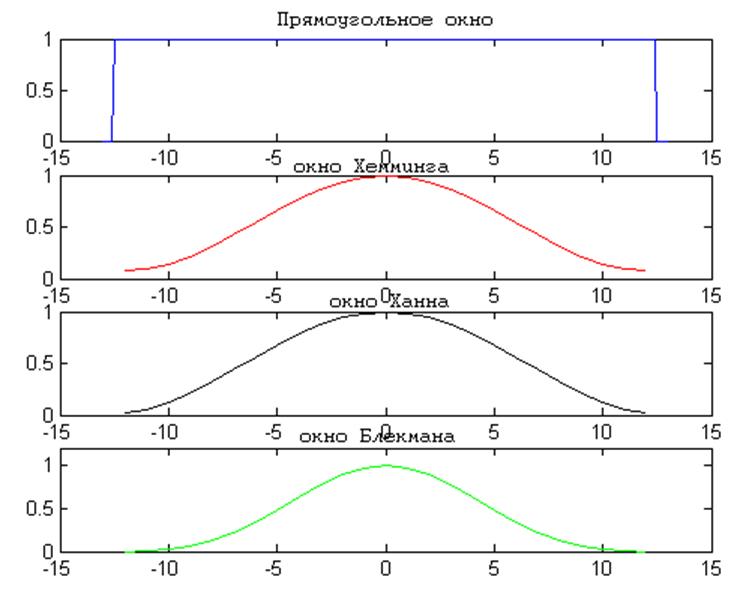
Рис.5
Рис.5 иллюстрирует графики окон Хемминга, Ханна, Блекмана и прямоугольного.
ЗАДАНИЕ № 6
Используя функцию DTFT() с 512 частотными отсчетами, вычислите ДВПФ оконных функций из предыдущего пункта и постройте в одном окне графики амплитудных спектров в шкале децибел.
[YWp,h1]=DTFT(Wp,512); %ДВПФ прямоугольного окна
[YWhm,h2]=DTFT(Whm,512); %ДВПФ окна Хэмминга
[YWhn,h3]=DTFT(Whn,512); %ДВПФ окна Ханна
[YWb,h4]=DTFT(Wb,512); %ДВПФ окна Блэкмана
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.