Изучение методов анализа и синтеза фильтров с конечной импульсной характеристикой с использованием сглаживающих оконных функций, страница 2

subplot(411); plot(h1,20*log10(YWp));

title('Прямоугольное окно')

axis([0 3.2 -50 50]);

subplot(412);

plot(h2,20*log10(YWhm),'-k'); title('окно Хэмминга')

axis([0 3.2 -100 50]);

subplot(413);

plot(h3,20*log10(YWhn),'-r'); title('окно Ханна');

axis([0 3.2 -100 50]);

subplot(414);

plot(h4,20*log10(YWb),'-g'); title('окно Блэкмана');

axis([0 3.2 -100 50]);

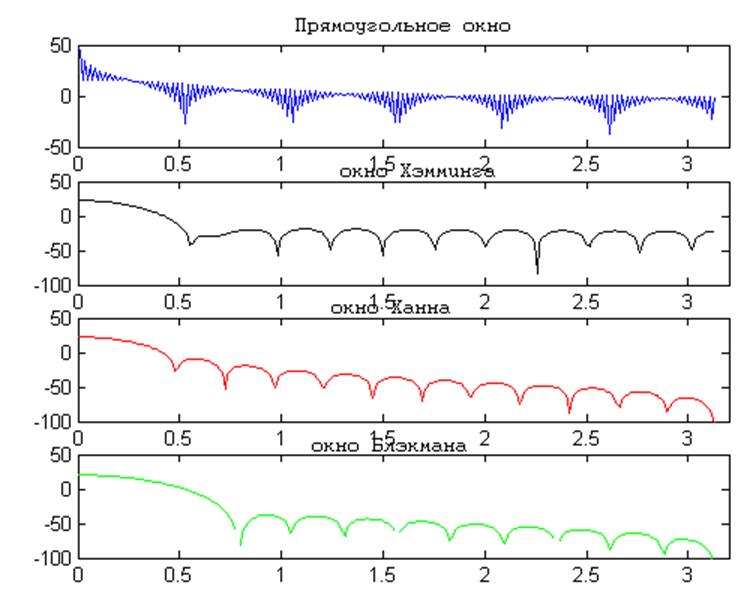
Рис.6

Данный рисунок представляет амплитудные спектры окон Хемминга, Ханна, Блекмана и прямоугольного в шкале децибел.

ЗАДАНИЕ № 7

Определите ширину главного лепестка и относительный уровень боковых лепестков в децибелах (относительно амплитуды главного лепестка). Составьте таблицу с измеренными и соответствующими теоретическими значениями величин и их разностями.

Определим требуемые величины для N=25, для этого воспользуемся функциями zoom и axis, и соответственно графиками, представленными на Рис.5.

Тип окна	Прямоугольное	Хэмминга	Ханна	Блекмана
Ширина главного лепестка (измеренная)	0.48	1.10	0.96	1.56
Ширина гл. лепестка (теоретическая)	0.503	1.005	1.005	1.508
Разность этих значений	0.023	0.095	0.045	0.052
Относительный уровень боковых лепестков (измеренный)	-12.9	-42.1	-31.3	-58.3
Относительный уровень боковых лепестков (теоретический)	-13	-41	-31	-57
Разность этих значений	0.1	1.1	0.3	1.3

По полученным результатом можно сделать вывод, погрешности измеренных значений ширины главного лепестка, они не превышают теоретические значения на величину 0.1.

Погрешности измеренных значений уровня боковых лепестков не превышают теоретические на величину 1.3. Погрешности можно объяснить не совершенностью измерений (т.к. измерения проводились «на глаз»), либо в системе Matlab.

ЗАДАНИЕ № 8

Постройте графики окон Кайзера  и их амплитудных спектров для   N = 25,

 β = 0, β = 1 и  β = 5. Используйте для этого функцию Matlab  kaiser(N, beta) и функцию DTFT() с 512 отсчетами частот.

N=25;%длина окна

K0=kaiser(N,0);%окно Кайзера при В=0

[HK0,w1]=DTFT(K0,512); %ДВПФ окна Кайзера при В=0

K1=kaiser(N,1); %окно Кайзера при В=0

[HK1,w2]=DTFT(K1,512); %ДВПФ окна Кайзера при В=1

K5=kaiser(N,5); %окно Кайзера при В=5

[HK5,w3]=DTFT(K5,512); %ДВПФ окна Кайзера при В=5

figure;

subplot(211); plot(K0);

title('b=0');

subplot(212); plot(w1,20*log10(HK0));

figure;

subplot(211); plot(K1);

title('b=1');

subplot(212); plot(w1,20*log10(HK1));

figure;

subplot(211); plot(K5);

title('b=5');

subplot(212); plot(w1,20*log10(HK5));

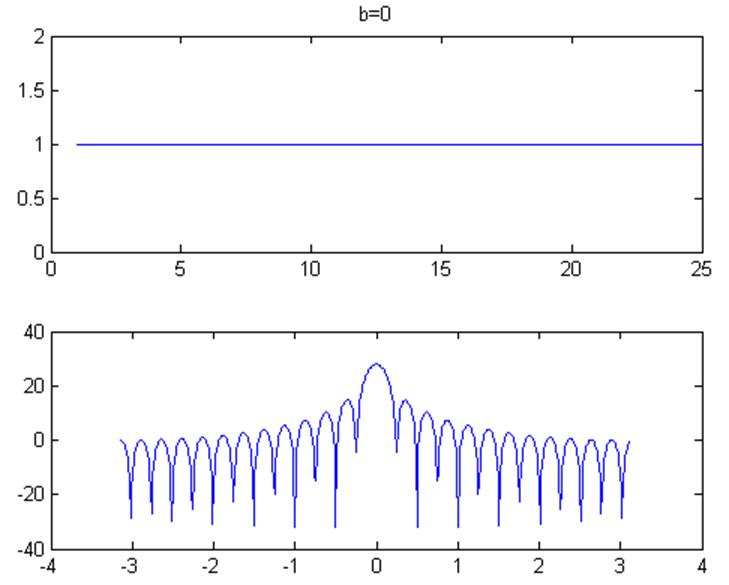
Рис.7

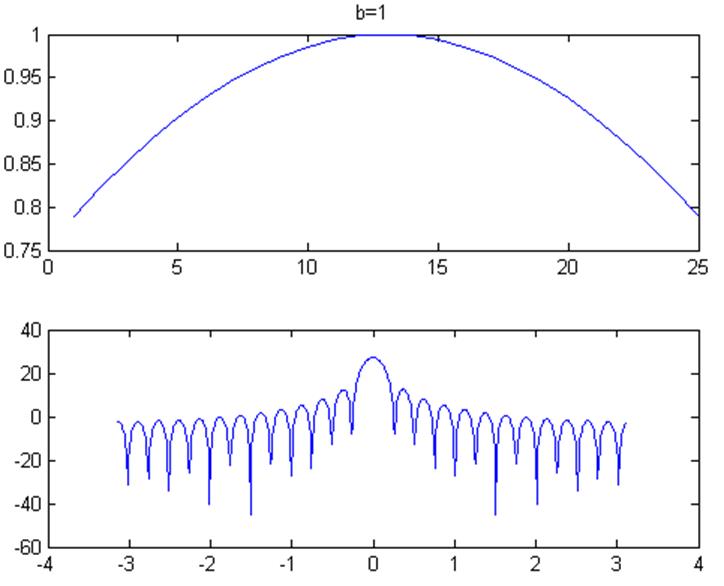
Рис.8

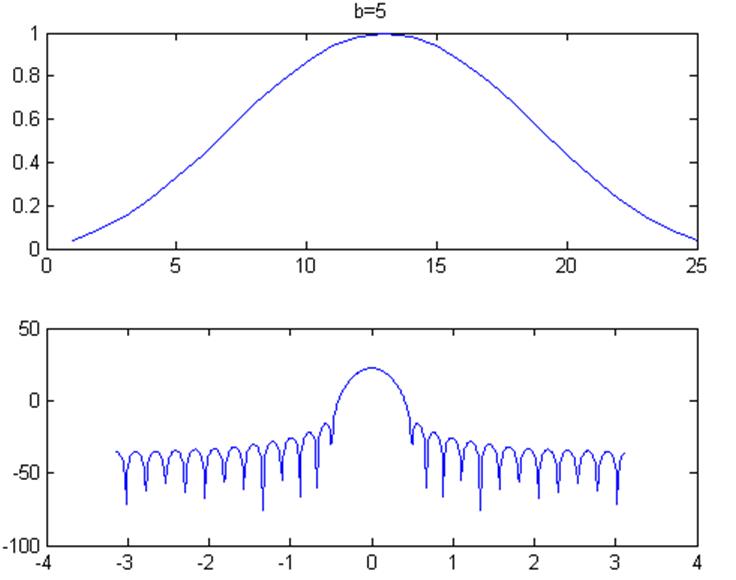
Рис.8

При увеличении параметра b форма окна становится более гладкой, так при b=0 вид окна  Кайзера близок к прямоугольному окну.

ЗАДАНИЕ № 9

Проведите расчет (синтез) фильтра по индивидуальному заданию. Постройте в заключение расчета график АЧХ спроектированного фильтра и проверьте его соответствие заданию.

Требования к фильтру:

                      

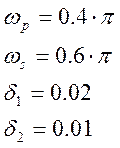
где
 граничная частота полосы пропускания

 - граничная частота полосы задерживания, 

 - допустимый уровень отклонений (пульсаций) АЧХ в полосе пропускания,

- допустимый уровень отклонений (пульсаций) АЧХ в полосе задерживания.

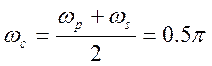
нормированная угловая переходная полоса  . Определим допустимый уровень пульсаций   как  или в децибелах  . Такому уровню ошибки аппроксимации идеальной АЧХ  фильтра соответствует окно Ханна, для которого  A = 44 дБ.

Определяем порядок фильтра с окном Ханна

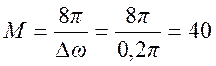
Окно Ханна фильтра

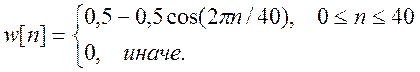
Импульсная характеристика рассчитанного фильтра

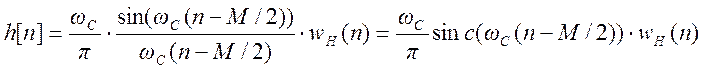
Построим АЧХ полученного фильтра, применив функцию DTFT к h[n].

n=0:39; %временной интервал

win=0.5-0.5*cos(pi.*n/20); %функция окна

y=0.5*sinc(0.5*(n-20)); % выражение ФНЧ

fil=y.*win; %ИХ фильтра

 [FIL1,w]=DTFT(fil,512); % Передаточная функция фильтра

plot(w,abs(FIL1))

grid

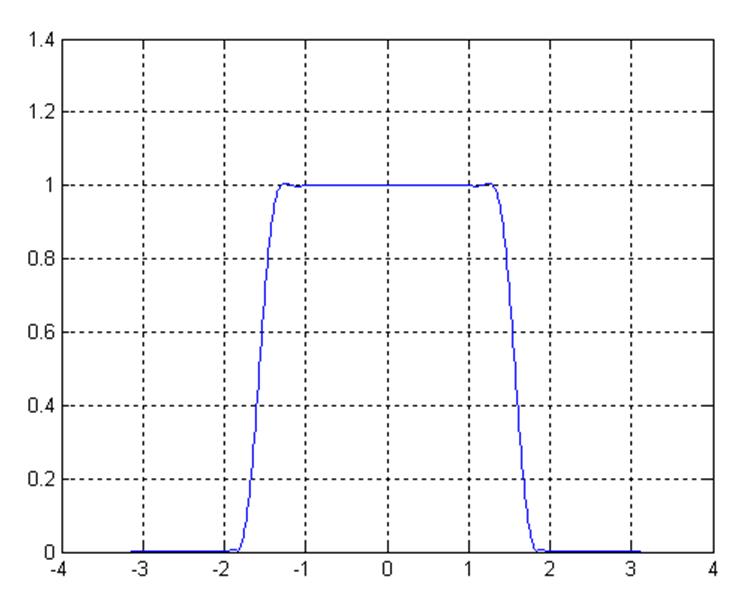
Рис.9

Теперь проверим подходит ли спроектированный фильтр заданным параметрам, для этого воспользуемся функциями zoom и axis, и увеличим соответствующие части графика.

Пульсации в полосе пропускания

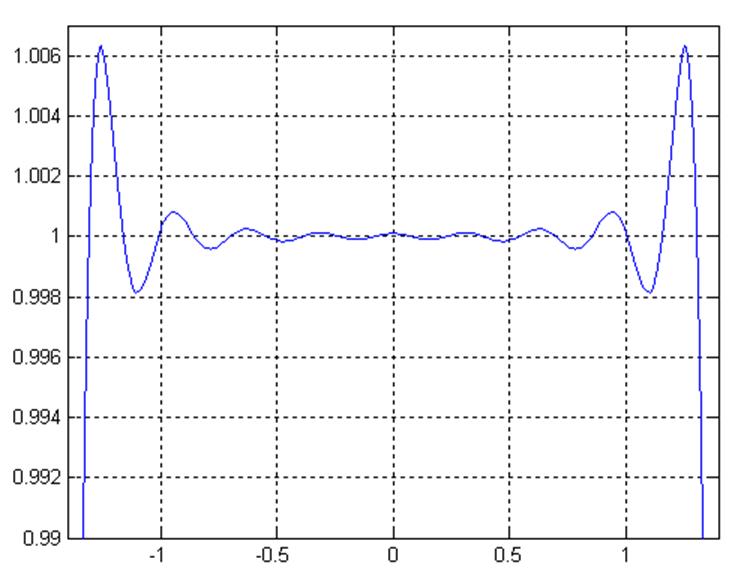
Рис.10

Из данного графика видно, что максимальное отклонение от единичного уровня составляет 0.006, что вполне удовлетворяет заданному допустимому уровню отклонений (пульсаций) АЧХ в полосе пропускания .

Также по данному  графику  определим граничную частоту полосы пропускания фильтра.

Она составляет приблизительно 1.25, что удовлетворяет заданному значению

Пульсации в полосе задерживания

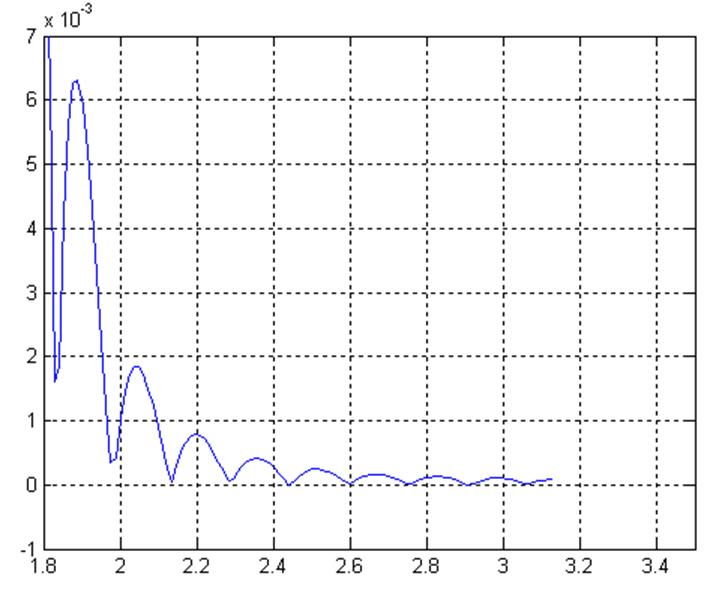
Рис.11

Из данного графика видно, что максимальное отклонение от единичного уровня составляет 0.0063, что вполне удовлетворяет заданному допустимому уровню отклонений (пульсаций) АЧХ в полосе задерживания .

 По данному  графику  определим граничную частоту полосы задерживания фильтра.

Она составляет приблизительно 1.83, что удовлетворяет заданному значению

Т.е. спроектированный фильтр удовлетворяет заданным значениям.

ЗАДАНИЕ № 10

Выполните фильтрацию сигнала speech спроектированным фильтром и оцените качество звучания сигнала до и после фильтрации.

>> S1=conv(nspeech2,fil);

>> sound(S1)

После фильтрации помехи практически отсутствуют.