Изучение дискретного преобразования Фурье и его свойств, алгоритмов быстрого преобразования Фурье, страница 2

Из условия БПФ N кратно 2, значит, можно свести вычисление ДПФ к вычислению в 2 точках. После вычисления преобразования в этих точках объединяем полученные последовательности в исходную последовательность.

          Т.о. видно, что для N=1021 скорость вычисления ПФ с помощью функции fft() превосходит скорость вычисления с помощью функции dftsum() почти в 2 раза. (fft - 0.0160 сек., dftsum – 0,0310 сек.).

5. Определение времени, за которое  вычисляется преобразование Фурье функциями dftsum и fft для N=1024.

Самое близкое значение к 1021 сверху, являющееся степенью 2, будет 1024.

Код MatLab:

dt=0.001;

t=0:dt:0.1023;

s=size(t);

xd=2*randn(size(t));

t1d=cputime;                 % Начало времени вычисления ДПФ

yd=dftsum(xd);             % Вычисление  ДПФ

t2d=(cputime - t1d);      % Конец времени вычисления

disp(t2d);

Вычисление ДПФ состоящего из 1024 точек (используя цикл):

Код MatLab:

% при помощи функции fft

N=2^10; dt=0.001;

t=0:dt:dt*(N-1);

xf=randn(size(t));       % Формирование случайной последовательности

t1f=cputime;               % Начало времени вычисления ДПФ

for n=0:999,

    yf=fft(xf);               % Вычисление  ДПФ

end

t2f=(cputime - t1f);    % Конец времени вычисления

disp(t2f/1000);

Сопоставим время, за которое было произведено БПФ c 1021 точек и 1024 точек.

Т.к. БПФ имеет наибольшее быстродействие при N кратному 2, то вычисление последовательности из 1024 точек проводиться быстрей, чем из 1021. А именно из 1021 - 0.0160 секунды, а из 1024 - 6.3000e-005 секунды, т.е. в 253 раза быстрее. При использовании же функции dftsum() при количестве точек равном 1024, скорость вычислений осталась  примерно такой же (0,0320 сек.).

6. Спектральный анализ  суммы сигнала и шума, основанный  на использовании ДПФ.

Код MatLab:

Fs=64;               % Частота отсчетов

f1=10;                % частоты  гармоник

f2=25;

N=128;              % число отсчетов сигнала

n=0:(N-1);

t=0:1/Fs:(N-1)/Fs;  % вектор времени

x=cos(2*pi*f1*t)+0.5*cos(2*pi*f2*t)+randn(1,length(t));    % сигнал для анализа

subplot(311), plot(t,x), grid                        % график сигнала

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Сигнал во временной области')

k=0:(N-1);

f=k*Fs/N;           % частотная шкала

X=fft(x);             % вычисление ДПФ

subplot(312), plot(f,abs(X)/Fs), grid

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный cпектр, положительные частоты')

% Построение спектра для положительных и отрицательных частот

k1=-N/2:(N/2-1);

f1=k1*Fs/N;

subplot(313), plot(f1,fftshift((abs(X))/Fs)), grid

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный cпектр')

xlabel('Частота,  Гц')

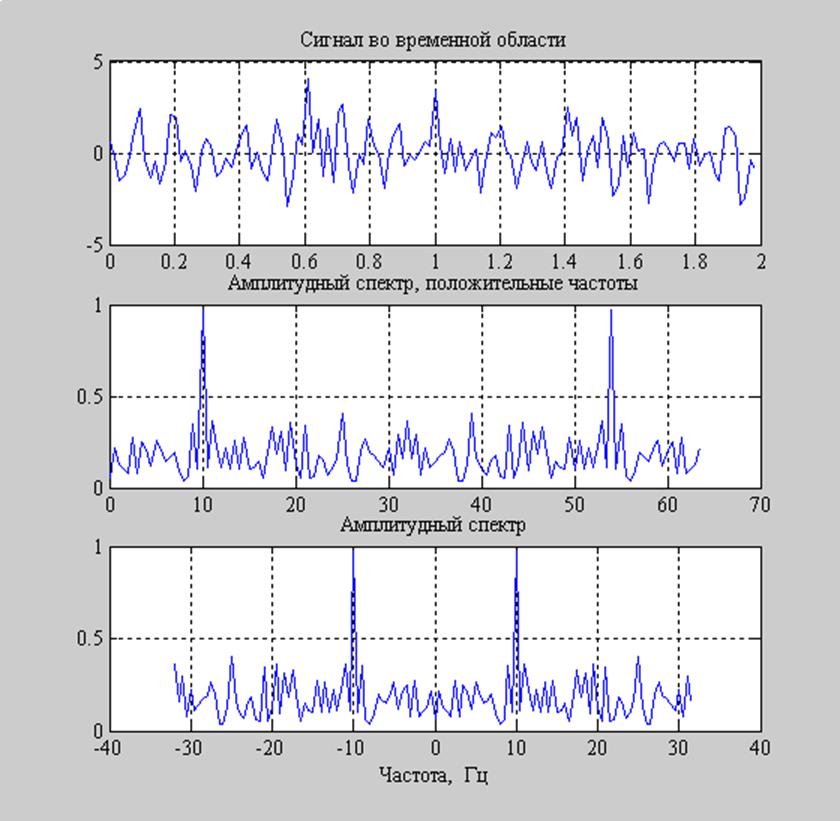
                     Рис. 9. График сигнала и его амплитудных спектров.

     Сигнал представляет собой  сумму двух гармоник и случайного шума. Для спектрального анализа  сигнала определим его графически. По построенным графикам  мы обнаруживаем гармонику с частотой 10 Гц и предположительно гармонику с частотой 25 Гц.

7.  Изучение влияния размера ДПФ на частотное разрешение.

Исходный сигнал: y=0.5cos(2pi*f1*t) + cos(2pi*f2*t).

Код MatLab:

N = input('N= ')

Fs=200;                                        % Частота отсчетов

f1=22;                                          % частоты  гармоник

f2=34;

M=16;                                                    % число отсчетов сигнала

n=0:(M-1);

t=0:1/Fs:(M-1)/Fs;                                 % вектор времени

x=0.5*cos(2*pi*f1*t)+cos(2*pi*f2*t);

subplot(211), stem(t,x), grid                   % график сигнала

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Сигнал во временной области')

 % Построение спектра для положительных и отрицательных частот

X=fft(x, N);                                   % вычисление ДПФ

k1=-N/2:(N/2-1);

f1=k1*Fs/N;

subplot(212), stem(f1,fftshift((abs(X))/Fs)), grid

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный cпектр')

xlabel('Частота,  Гц')

N=16

N=64

N=128

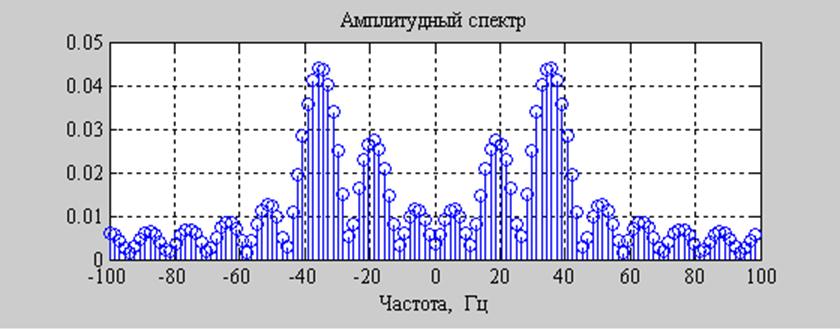
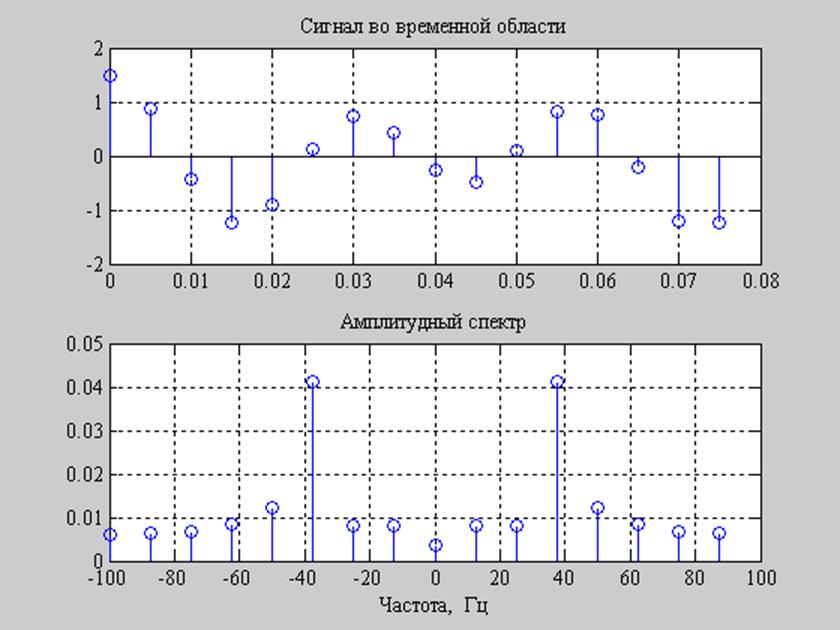
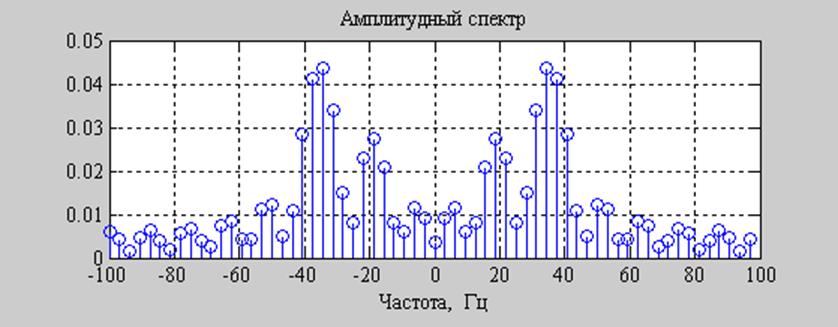
Рис. 10. График сигнала и его спектров при N-точечном ДПФ.

При увеличении N расстояние между соседними  разрешаемыми частотами уменьшается, спектр становится более частым. Т.о. можно нагляднее наблюдать характер амплитудных спектров.

8. Обработка анализируемого сигнала при помощи оконной функции.

Код MatLab:

N = 64;                               % размер ДПФ

Fs=200;                              % Частота отсчетов

f1=22;                                 % частоты  гармоник

f2=34;

M=16;                                 % число отсчетов сигнала

n=0:(M-1);

t=0:1/Fs:(M-1)/Fs;                       % вектор времени

x=0.5*cos(2*pi*f1*t)+cos(2*pi*f2*t);

x_w=(x'.*hamming(length(x)))';

figure(1);

subplot(211), stem(t,x), grid     % график сигнала

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title(' Исходный сигнал')

subplot(212), stem(t,x_w), grid  

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Сигнал, сглаженный функцией hamming')

figure(2);

% Построение спектра для положительных и отрицательных частот

X=fft(x, N);                         % вычисление ДПФ

k1=-N/2:(N/2-1);

f1=k1*Fs/N;

subplot(211), stem(f1,fftshift((abs(X))/Fs)), grid

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный спектр исходного сигнала')

xlabel('Частота,  Гц')

X_w=fft(x_w, N);               % вычисление ДПФ

subplot(212), stem(f1,fftshift((abs(X_w))/Fs)), grid

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный спектр сигнала, сглаженного функцией hamming')

xlabel('Частота,  Гц')

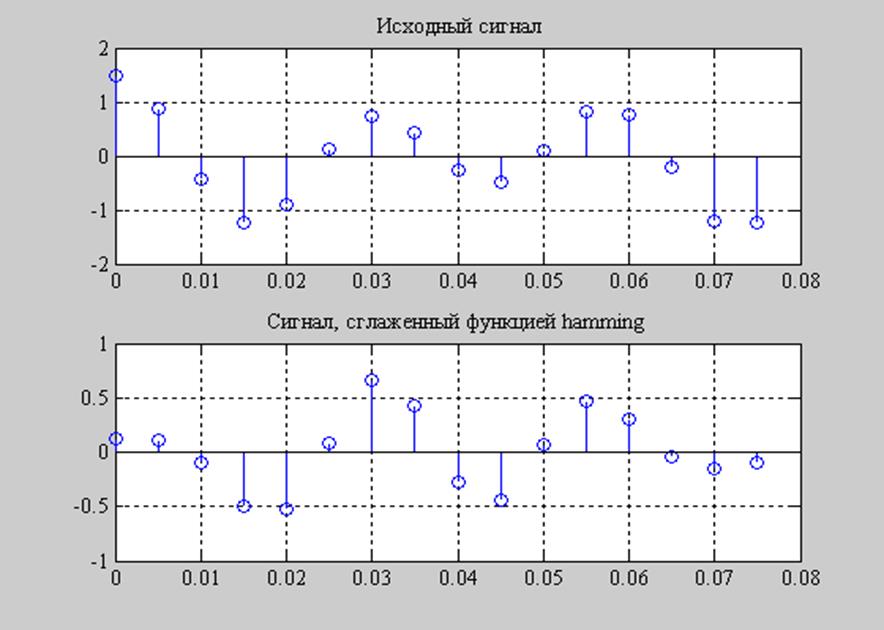
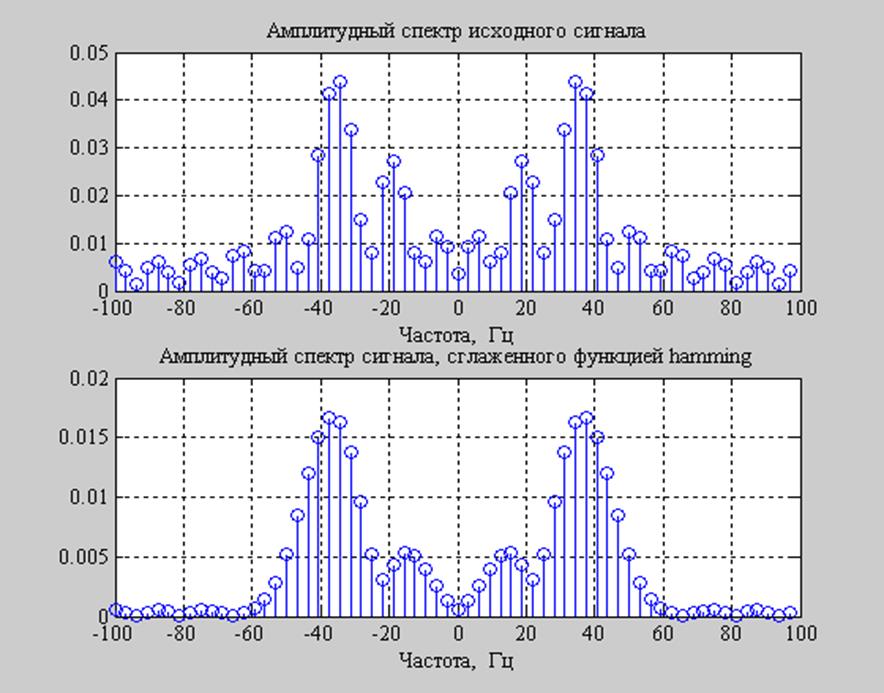
Рис. 11. Обработка исходного сигнала оконной функцией.

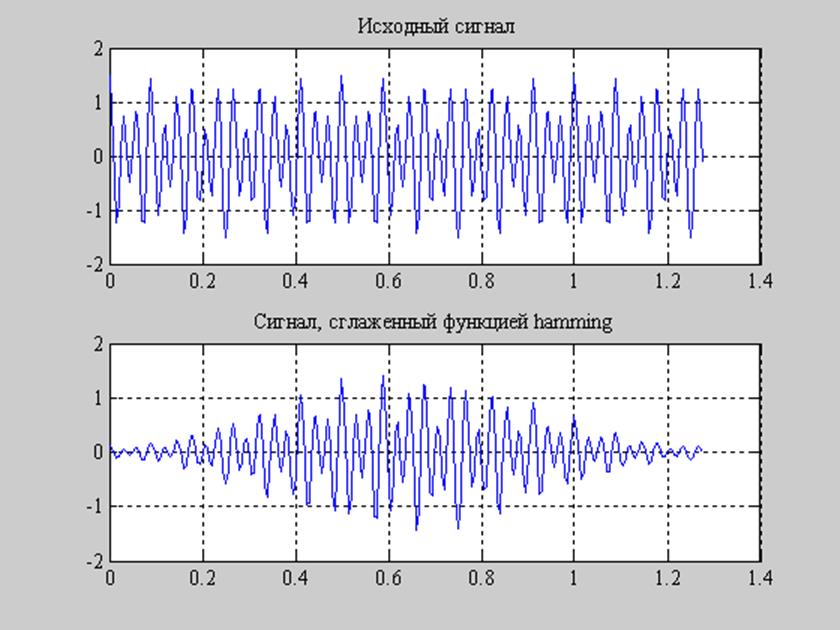
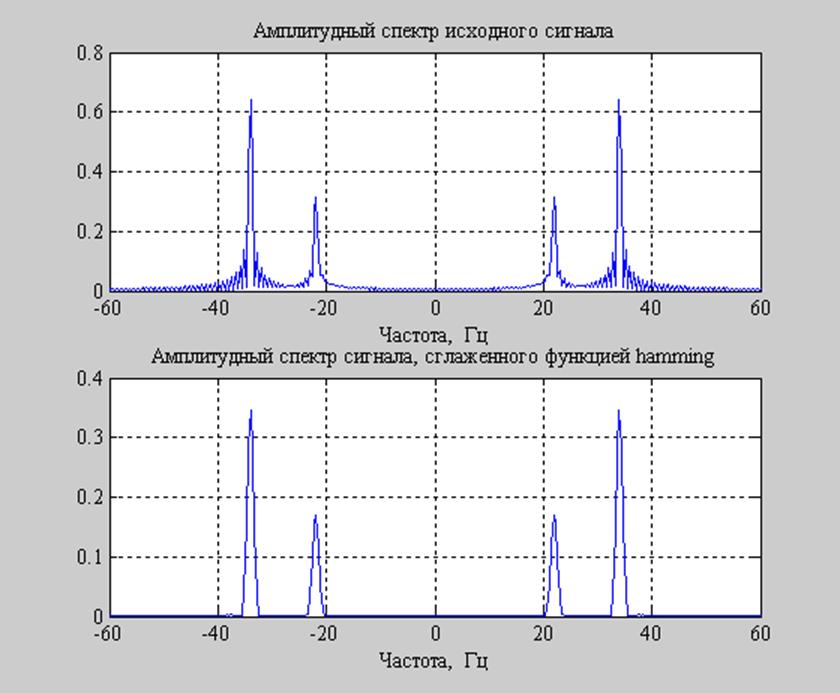
Рис.12. Оконная обработка исходного сигнала при N=512, M=256.

У оконной функции hamming  99,96%  всей энергии заключено в главном лепестке. Т.о. После обработки исходного сигнала функцией Хэмминга, сигнал серьезным образом сглаживается, у спектра пропадают ненужные пульсации. Значит, оконная функция hamming может с успехом применяться на практике, когда нужно избавиться от шумов, сделать сигнал более “чистым”. Кроме того, функция Хэмминга часто используется для уменьшения влияния растекания спектра.

9. Программа для вычисления и вывода графиков во временной и частотной области фрагмента речевого сигнала.

Код MatLab:

[y,Fs]=wavread('MySpeech.wav', 1)

y =

 0     0

Fs =

 44100

Fs=44100;                                               % Частота отсчетов

y=wavread('MySpeech.wav');                % сигнал

N = length(y);

n=-N/2:N/2-1;

n1=n+N/2;

Y=fft(y);                                                 % Вычисление  ДПФ 

Yp=fftshift(Y);                                       % Сдвиг ДПФ

f=n*Fs/N;                                               % Частотная шкала

figure(1), subplot(211), plot(n1/Fs,y,'ko-');

grid;

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10);

xlabel('Время, с');

title(' Сигнал ');

subplot(212), plot(f,abs(Yp/N));

grid;

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10);

xlabel('Частота, Гц');

title('Амплитудный спектр сигнала');

figure(2), subplot(111), specgram(y(:,1),[],Fs);

title('спектрограмма звукового сигнала ');

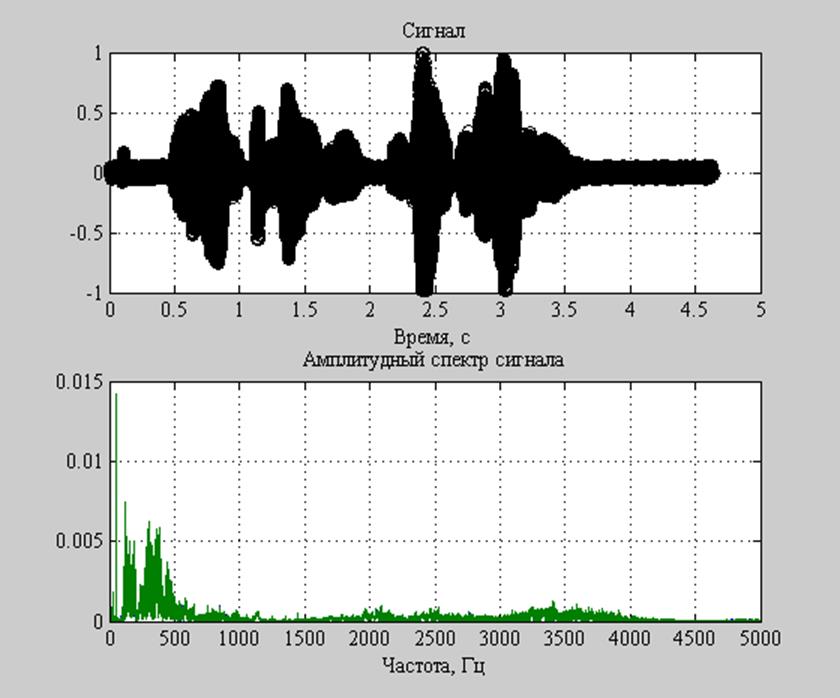
Рис.13. Звуковой сигнал и его амплитудный спектр.

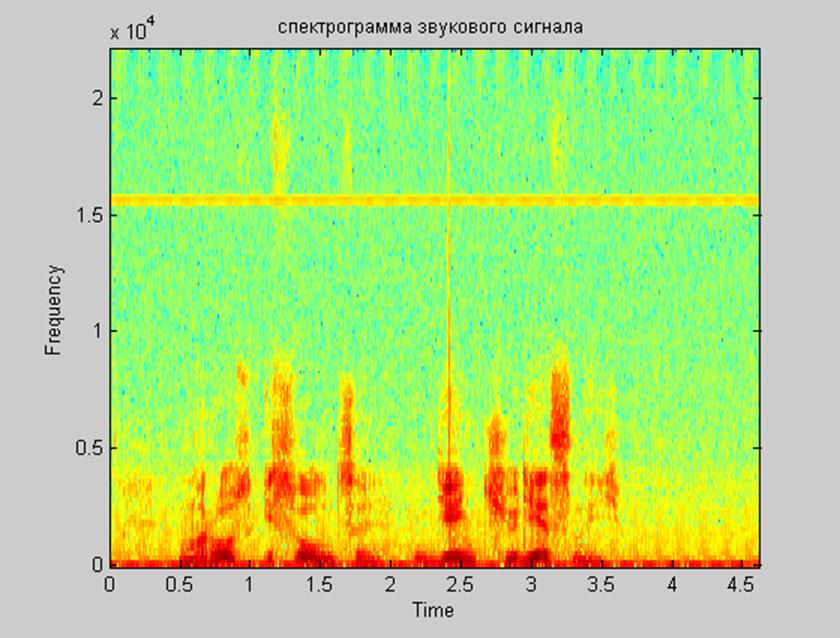
Рис.14. Спектрограмма сигнала.

Спектрограмма является графическим представлением звуковых колебаний. Фактически — это спектрально-временное представление звука.

На спектрограмме значения амплитудного спектра отображаются с помощью цвета. Чем больше амплитуда, тем более ярким оранжевым цветом она отображается. Чем меньше амплитуда спектральной составляющей, тем более темно-голубой у нее цвет. Т.о. можно выявить определенные соответствия между амплитудным спектром сигнала и его спектрограммой.

Также можно проследить соответствия между спектрограммой и графиком исходного сигнала. Речь сигнала отражается на спектрограмме в виде областей оранжевого цвета в соответствующие моменты времени. По спектрограмме можно увидеть, что максимальной амплитуды сигнал достигает во временной период около 2,4 сек.