Определение линейной дискретной системы. Поиск Z-преобразования сигнала. Определение сигнала x[n] во временной области по заданному Z-преобразованию

Задача 1.  На рис.1 показан дискретный по времени сигнал  x [n]

 

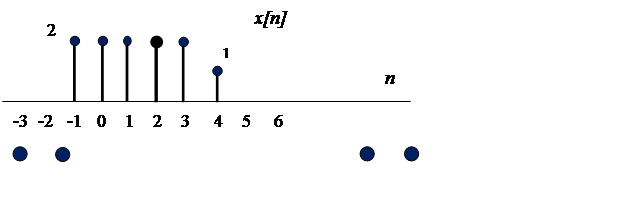Рис.1

Изобразите  график сигнала:

.

Решение:

График функции получаем из графика симметричным отражением относительно оси Oy (рис.2).

 

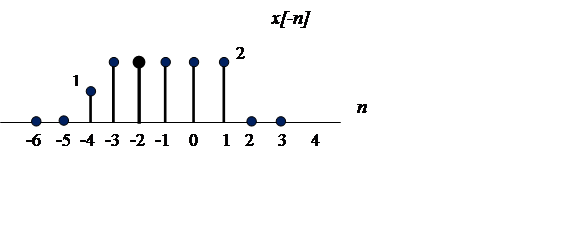Рис.2

График функции  получаем из графика параллельным переносом влево на 4 единицы (рис.3).

 

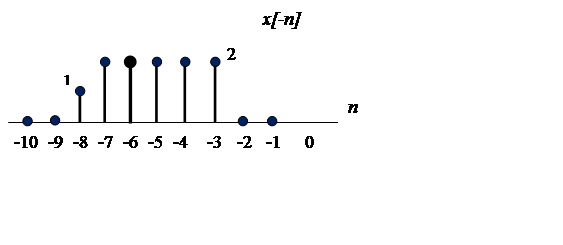Рис.3

Ответ: график функции изображен на рис.3.

Задача  2.  Определите, является ли дискретная система с заданным уравнением линейной, стационарной (инвариантной во времени), физически реализуемой (каузальной) и устойчивой:

.

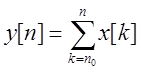Решение:

а.  Положим 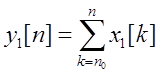, 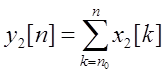. Если , то 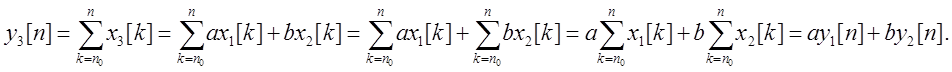Следовательно, система линейная.

б.  Система стационарна, если временной сдвиг сигнала на входе вызывает такой же сдвиг сигнала на выходе.  Пусть 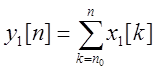. - сигнал на входе со сдвигом. При этом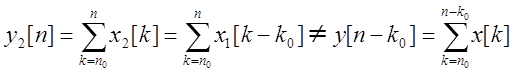 (неравенство можно обнаружить, взглянув на количество слагаемых в первой и второй сумме -и , соответственно). Таким образом, система не является стационарной.

в.  Система называется каузальной, если выходной сигнал зависит только от предыдущих и настоящих значений сигнала, но не от будущих. Так как это условие соблюдается для исходной системы, она является каузальной.

г.  Система называется устойчивой, если ограниченному входному сигналу соответствует ограниченный выходной сигнал. Если  для всех , то 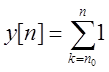 и выход системы неограниченно возрастает. Следовательно, исходная система – неустойчивая.

Ответ: система является линейной, нестационарной, каузальной, неустойчивой.

Задача 3.  Найдите Z – преобразование сигнала:

.

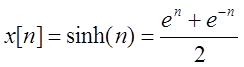Решение:

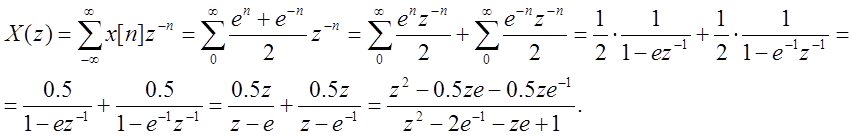
Ответ: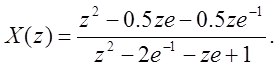

Задача  4.  Определите сигнал  x[n] во временной области по заданному         Z -  преобразованию:

.              

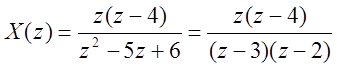Решение:

Вычислим обратное Z-преобразование с помощью теоремы о вычетах. Уравнение имеет простые полюса в точках

Вычет в точке

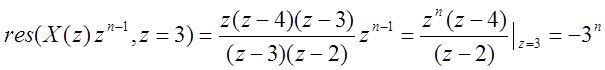
Вычет в точке

.

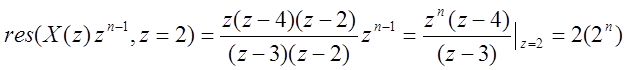
Ответ:   .

Задача  5.  Система задана передаточной функцией  H(z). Найдите нули и полюса системы, изобразите их на графике. Определите, является ли система устойчивой?  Найдите импульсную характеристику системы.

.

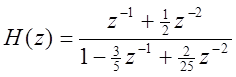Решение:

Преобразуем исходную дробь, умножив числитель и знаменатель на и разложив знаменатель на множители:

.

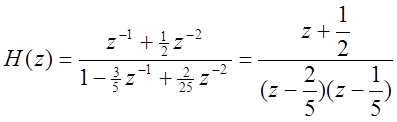Нули функции: . Полюса функции: .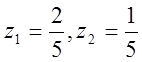

Изобразим полюса на графике с помощью пакета Matlab, используя скрипт-файл 1, приведенный в приложении (рис.4).

script-file 1:

num = [1 0.5];

den = [1 -0.6 0.08];

Z = roots(num);

P = roots(den);

zplane(Z, P);

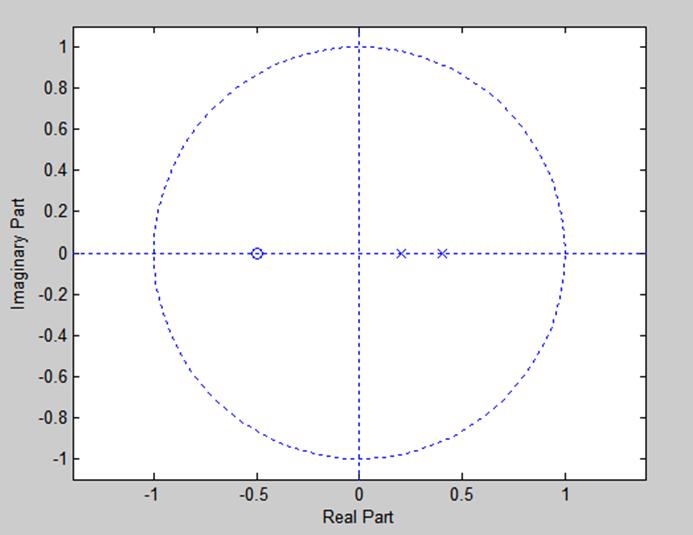
Рис. 4

Из графика видно, что полюса лежат в пределах единичной окружности, т.е. система устойчива.

Найдем импульсную характеристику системы. Для начала, разложим преобразованную исходную дробь на простые.

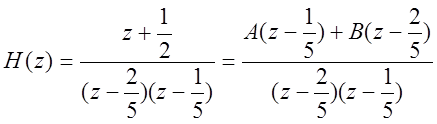
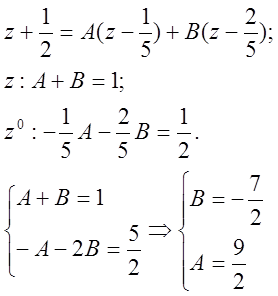
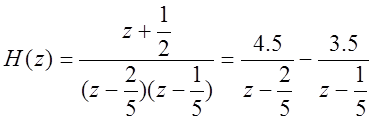
Найдем обратные Z-преобразования получившихся дробей.

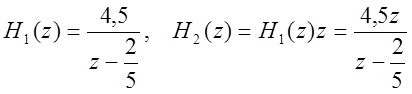
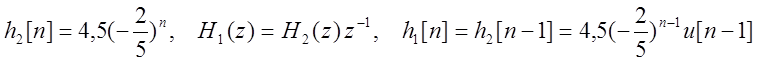
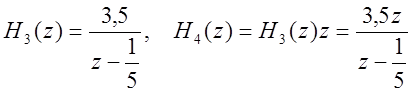
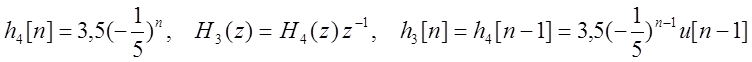
Импульсная характеристика системы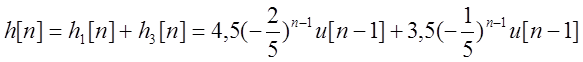 

Ответ: нули функции: , полюса функции: 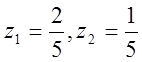. Нули  полюса изображены на рис.4. Система является устойчивой. Импульсная характеристика системы: .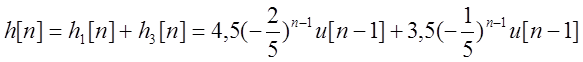

Задача  6.  Для системы с заданным уравнением найдите передаточную функцию, а также АЧХ и ФЧХ и постройте их графики:

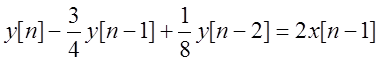
Решение:

Возьмем Z-преобразование от левой и правой частей уравнения.

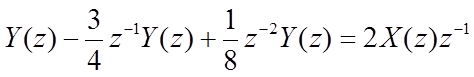
Передаточная функция системы: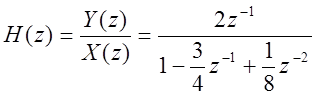    

Частотная характеристика: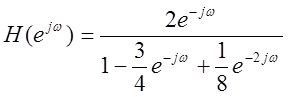    

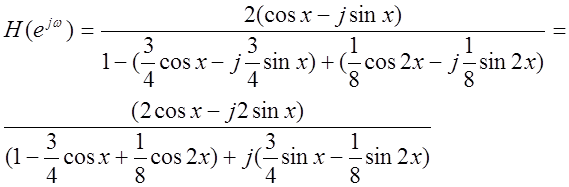
Для простоты дальнейших преобразований заменим:

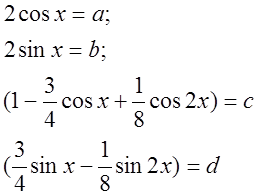
Найдем АЧХ: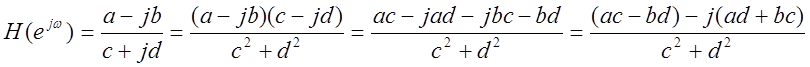

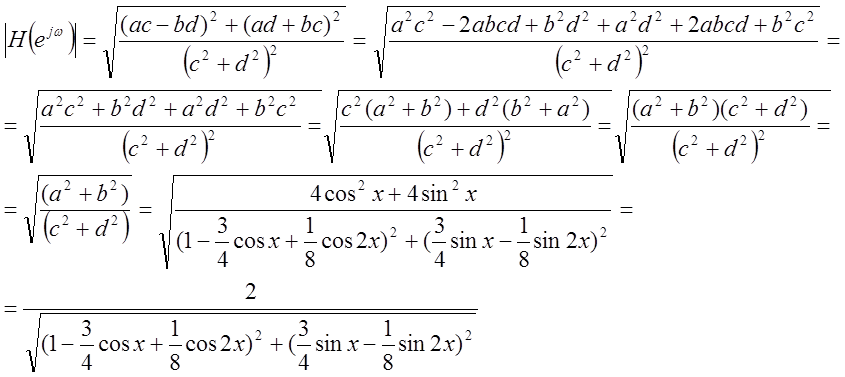
Найдем ФЧХ:

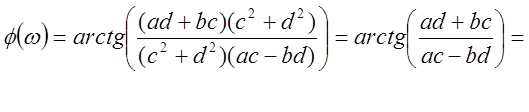
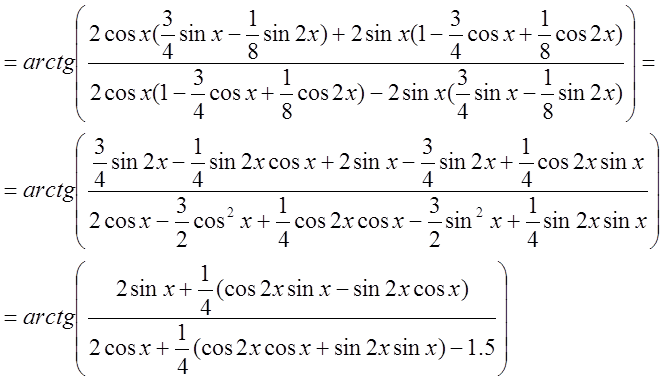
Построим график АЧХ и ФЧХ, используя скрипт-файл 2(рис.5).

script-file 2:

num = [2];

den = [0.125 -0.75 1];

freqs(num,den)

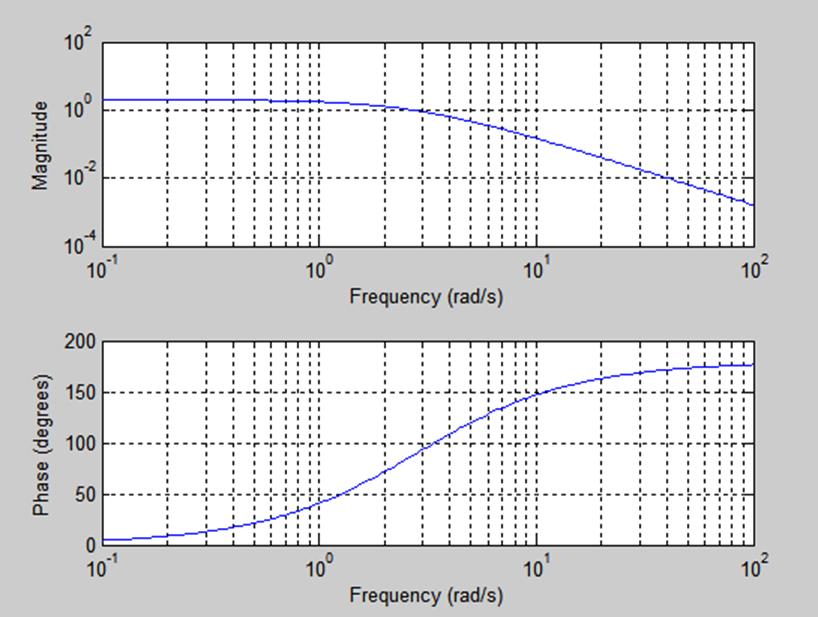
Рис.5

Задача  7.  Входной сигнал системы ,  при этом выходной сигнал
  .

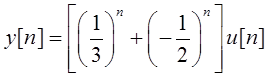Найдите:
а)  передаточную функцию системы,
б)  импульсную характеристику системы,
в)  разностное уравнение системы.

Решение:

Для нахождения H(z)  определим Z – преобразования заданных x[n] и y[n]:

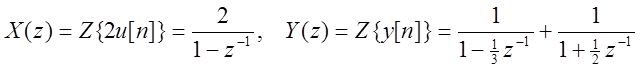
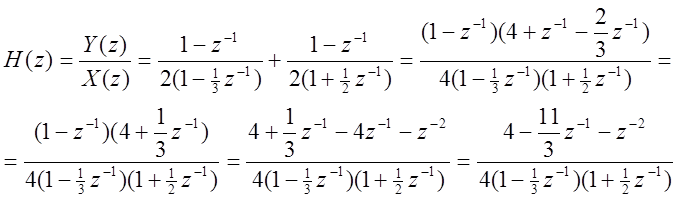
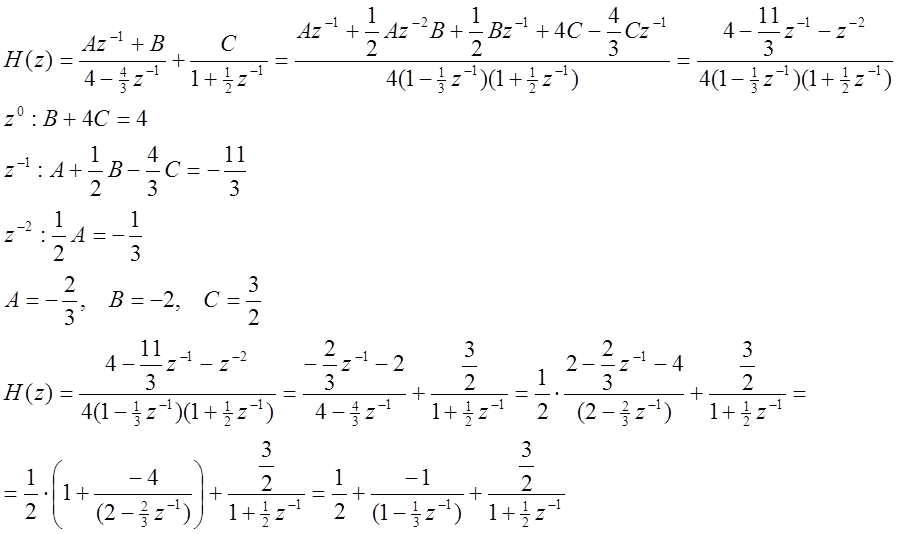
Выполняя обратное  Z – преобразование  от H(z) как суммы простых дробей, находим импульсную характеристику системы в виде:

.

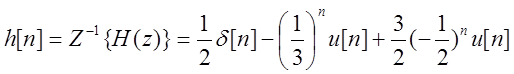Для получения уравнения системы перепишем H(z) в виде:

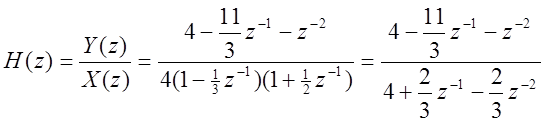
Отсюда  .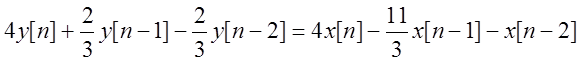

Ответ: передаточная функция: ;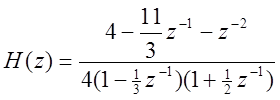

импульсная характеристика: ;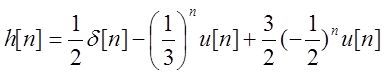

разностное уравнение:.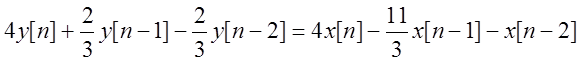

Задача  8.   Рассчитайте  аналоговый ФНЧ  Баттерворта, т.е.  определите передаточную функцию фильтра для заданной в таблице 1 спецификации.  Постройте графики АЧХ и ФЧХ спроектированного фильтра.

№ вар-та	Частота среза, Гц	Граничная частота полосы задерживания, Гц	Максим. допустимое отклонение в полосе пропускания, Дб	Минимально допустимое ослабление в полосе задерживания, Дб
2	100	300	3	20

Последовательность расчета фильтра:

1. Определение порядка фильтра.
2. Нахождение полюсов фильтра.
3. Определение передаточной функции нормированного ФНЧ.
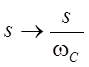4. Частотное преобразование нормированного ФНЧ в требуемый подстановкой   в передаточную функцию нормированного ФНЧ.

;

;

Выберем частоту дискретизации (отсчетов)  в соответствии с требованиями теоремы отсчетов равной 10000 Гц, при этом частота Найквиста  равна 5000 Гц. Нормированные граничные частоты полосы пропускания и полосы задерживания окажутся  равными  0,2 Гц/отсчет и 0,5 Гц/отсчет соответственно.

Для определение порядка фильтра воспользуемся функцией buttord:

[n,Wn] = buttord(0.02*pi,0.06*pi,3,15,'s')

Результат выполнения:

n =

     2

Wn =

    0.0801

Порядок фильтра - второй.

Воспользуемся функцией  [z, p, k,] = buttap(N) для вычисления полюсов p фильтра .

[z, p, k,] = buttap(2)

z =

     []

p =

  -0.7071 + 0.7071i

  -0.7071 - 0.7071i

k =

     1

Т.к. фильтр n=2, то передаточная функция нормированного ФНЧ Баттерворта 2 – го порядка  .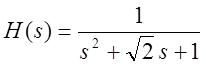

Для построения АЧХ и ФЧХ фильтра выполним следующий скрипт:

[b, a] = butter(2, 0.0801); [h,w]=freqs(b,a);

subplot(211), semilogx(w/2/pi, abs(h)), grid

subplot(212), semilogx(w/2/pi, unwrap(angle(h))*180/pi)

 Результат выполнения:

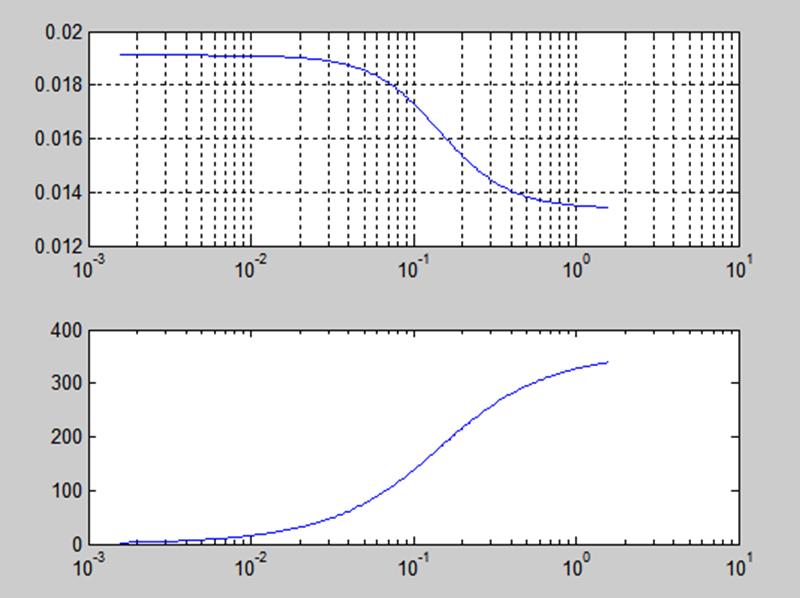
Частотное преобразование нормированного ФНЧ в требуемый подстановкой 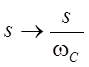  в передаточную функцию нормированного ФНЧ.

 Передаточная функция .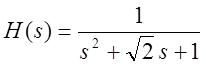

Угловая частота среза целевого  ФВЧ . Выполняя подстановку 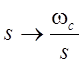  и  последующие преобразования,  получим передаточную функцию ФВЧ в виде

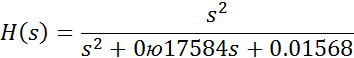
9. .    Используя метод инвариантного преобразования импульсной характеристики,  выполните преобразование фильтра, полученного в предыдущей задаче,  в цифровой ФНЧ.  Представьте графики АЧХ и ФЧХ цифрового фильтра.  Кратко охарактеризуйте  преимущества цифровых фильтров  по сравнению с аналоговыми.

Синтез целевого фильтра выполним на основе расчета аналогового прототипа и его дискретизации, т.е. перехода к цифровому фильтру с помощью метод инвариантного преобразования импульсной характеристики.

Для фильтра второго порядка имеем четыре полюса, из них два полюса в левой полуплоскости, которые и используем для получения передаточной функции  фильтра

.

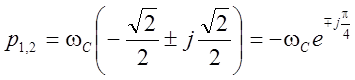Отсюда передаточная функция аналогового прототипа

.

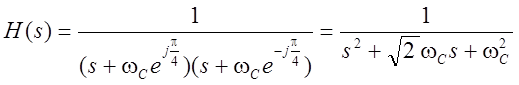Для  перехода к цифровому фильтру по условию задачи  используем метод инвариантного преобразования импульсной характеристики, при котором в качестве его импульсной характеристики берутся отсчеты импульсной характеристики аналогового прототипа.

При этом методе передаточная функция аналогового фильтра записывается в виде суммы простых дробей       .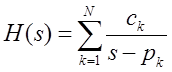

Для данного случая

.

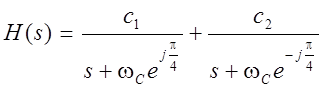Находим константы разложения на простые дроби

,

.

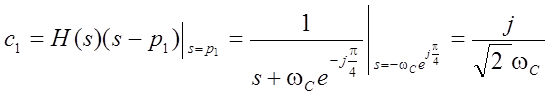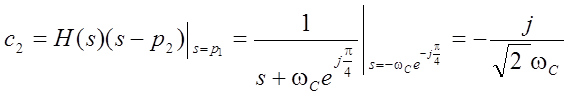Таким образом,

.

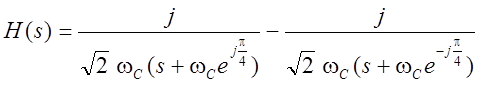Передаточная функция цифрового фильтра  при данном методе дискретизации аналогового  фильтра представляется

как 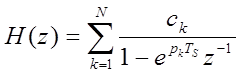 ,   где  T_S  - интервал дискретизации (отсчетов).

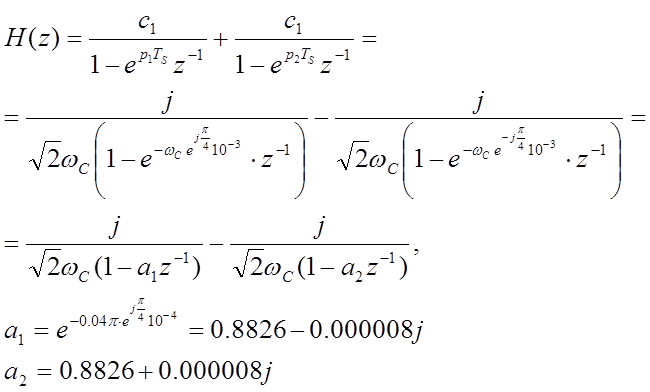
После преобразования

 

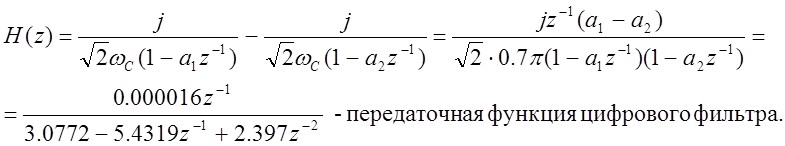
АЧХ и ФЧХ получившегося фильтра

num = [0 0.000016 0];

den = [2.397 -5.4319 3.0772];
subplot(2,1,1);
[H,F] = freqz(num,den,10000,10^4);
plot(F, abs(H))
set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)
title('АЧХ цифрового фильтра');
xlim([0 1000])
subplot(2,1,2);
plot(F, angle(H))
set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)
title('ФЧХ цифрового фильтра');
xlabel('Частота, Гц');

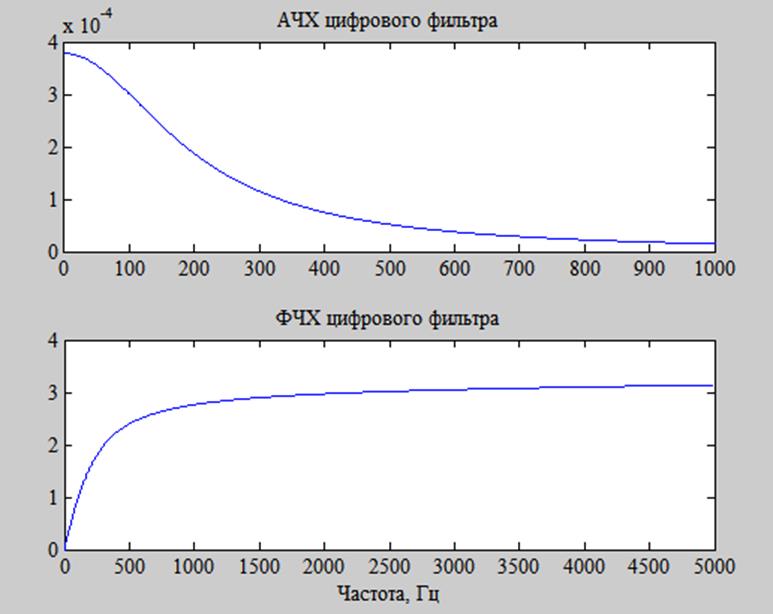
Преимуществами цифровых фильтров перед аналоговыми являются:

§  Высокая точность (точность аналоговых фильтров ограничена допусками на элементы).

§  Стабильность (в отличие от аналогового фильтра передаточная функция не зависит от дрейфа характеристик элементов).