Определение линейной и инвариантной во времени дискретной системы. Определение выходного сигнала системы. Поиск импульсной характеристики, АЧХ и ФЧХ системы

ЗАДАЧИ   10

учеб.  пособие  Г&Щ,   ч.2,  стр. 49 – 70.

Примеры  решения  задач.

1.  Является ли линейной и инвариантной во времени дискретная  система с уравнением  ?
Решение.
Для рассматриваемой системы  .  При  входном сигнале в виде линейной комбинации    x₁[n]  и  x₂[n]     выходной сигнал   .  Следовательно, система является линейной. Но эта система – неинвариантная во времени (нестационарная). Действительно, если входной сигнал  , то выходной сигнал  .
Но для инвариантной во времени системы 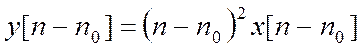 .  Поскольку  , то система – неинвариантная.

2.  Линейная дискретная инвариантная во времени система  S имеет следующие пары сигналов  вход – выход  (рис. 9.1):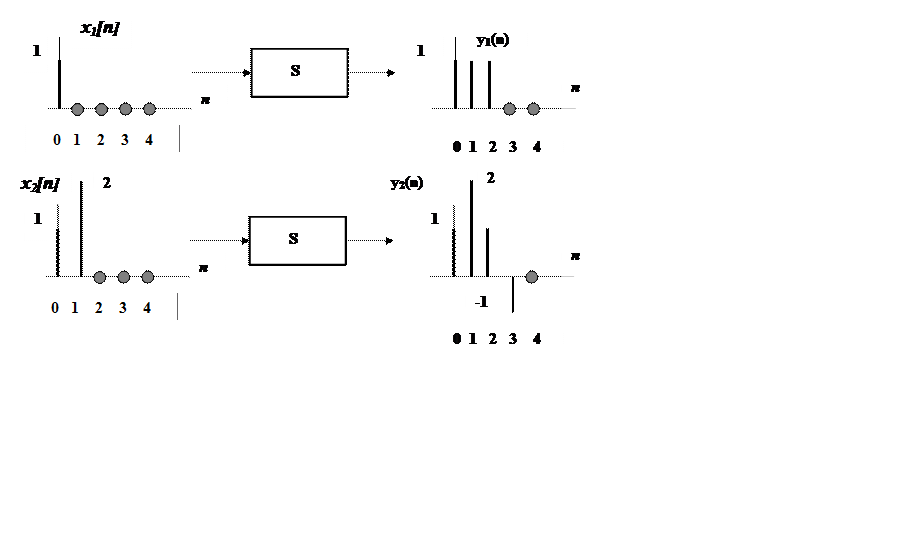  

Рис.  9.1.

Определите отклик системы на входной сигнал  в виде сдвинутого единичного импульса  .
Решение.
Представим входной сигнал   в виде линейной комбинации  x₁[n]  и   x₂[n]
.  Следовательно, исходя из линейности системы, её выходной сигнал будет иметь вид  , т.е. .

3.  Входной сигнал и импульсный отклик системы приведены на рис. 9.2. Определить выходной сигнал системы.

Рис. 9.2.

Решение.

Используем выражение дискретной свертки    .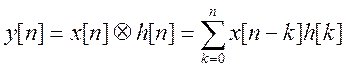

Вычисление производим по интервалам значений n:

1.    ,

2.    ,

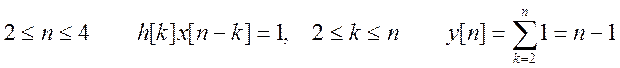3.    ,

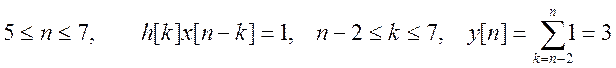4.    ,

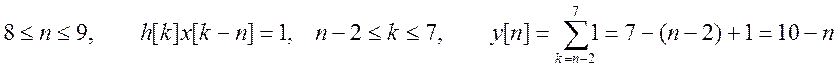5.    .

График выходного сигнала

Рис. 9.3.

4.  Найдите импульсную характеристику, АЧХ и ФЧХ системы  с  разностным уравнением     .
Решение.
В данном случае имеем  КИХ-систему  первого порядка.
Импульсная характеристика  системы .
Передаточная функция  .
Частотная характеристика  .

АЧХ  системы: ,  ФЧХ .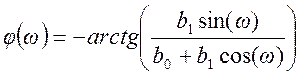
Графики АЧХ  и ФЧХ для  b₀ = 1,2,  b₁ = 0,8  (рис. 9.4)

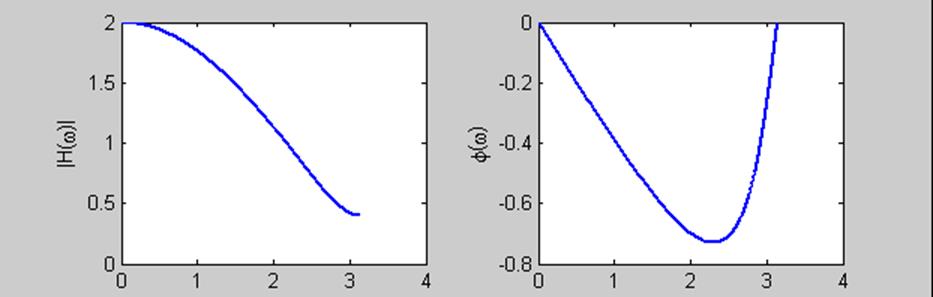
Рис. 9.4.

5.  Найдите импульсную характеристику  фильтра, передаточная функция которого задана  в виде
                                                 .
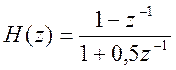Решение. 
Первый  метод.  Выразим  уравнение системы, исходя из передаточной функции
                                     ,
                                       или
                                     .
Импульсная характеристика – это реакция системы на единичный импульс 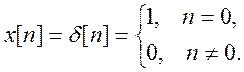      Подавая этот импульс на вход при нулевых начальных условиях,   находим
Это рекурсивный способ вычисления импульсной характеристики по отсчетам.

6.  Второй метод.   Импульсная характеристика – это обратное Z – преобразование от передаточной функции H(z).  Запишем передаточную функцию в виде целой части и правильной  дроби         .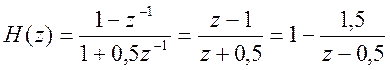

 Найдем обратные Z - преобразования  слагаемых.   .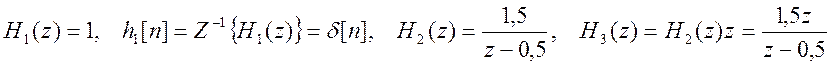
.
Импульсная характеристика системы  .
Значения h[n]:    .

По найденному выражению можно вычислить  h[n]  для любого  значения  n ( нерекурсивный способ).

7.  Импульсная характеристика системы  , где  u[n]- дискретная единичная ступенчатая функция. Найдите выходной сигнал этой системы при входном сигнале 
Решение.
Перейдем в z-область, при этом  нетрудно получить, что
,    .  

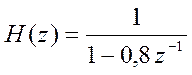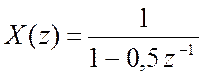 Выход  системы 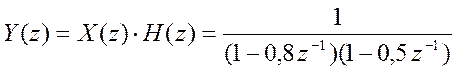 .  Разложим это выражение на простейшие дроби,     .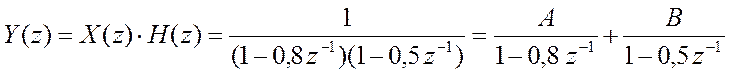
Числители дробей
,

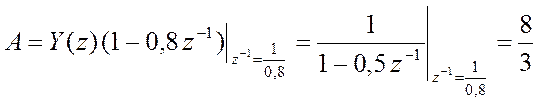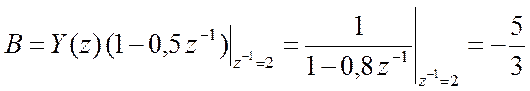       .        Тогда
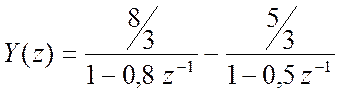.  Выполняя обратное  Z – преобразование, опираясь при этом на Z – преобразование показательной функции, находим
.

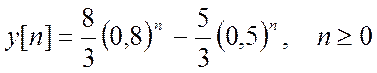Примечание. Возможно решение во временной области с помощью дискретной свертки.

Для этого определяем импульсную характеристику  и входной сигнал как функцию времени  . Далее вычисляется свертка этих последовательностей.   См  задачу 3.

8.       Определите передаточную функцию и частотные характеристики системы второго порядка с уравнением
                    .
Решение.
Это БИХ - система второго порядка.  Возьмем  Z- преобразование от левой и правой части уравнения

. 

Отсюда передаточная функция системы

.

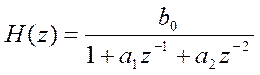Частотная  характеристика                              .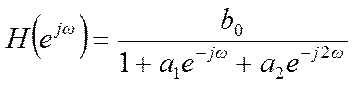

Полюса  системы    .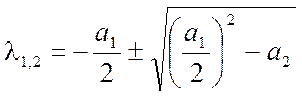

Для действительных коэффициентов  a₁  и  a₂   полюса могут быть действительными  или комплексно-сопряженными

.

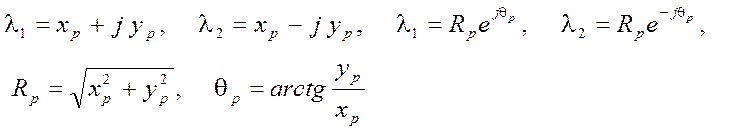Полюсно - нулевое представление  передаточной функции

.

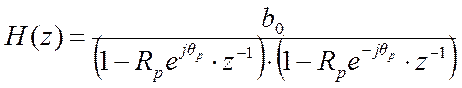Отсюда, используя формулу Эйлера для комплексной экспоненты и проводя  простые преобразования, получаем выражение АЧХ в виде

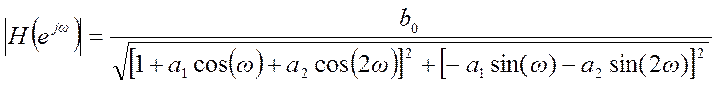
Фазо – частотная характеристика

.

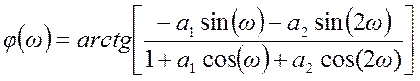При этом                                                         

.

На  графиках (рис. 9.5)  приведен вид АЧХ и ФЧХ для коэффициентов  b₀ = 2,   a₁ =0,4   a₂ =0,8.

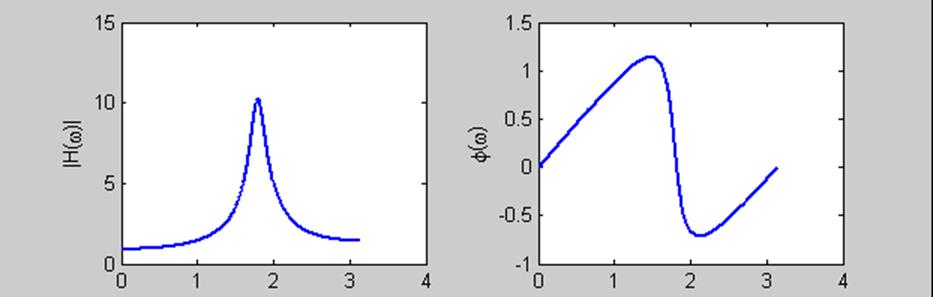
Рис. 9.5.

При данных параметрах  АЧХ системы имеет резонансный характер.

8.      Система имеет передаточную функцию  вида 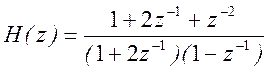 . Найдите импульсную характеристику системы и выходной сигнал при входе .

Решение.

            Для определения импульсной характеристики разложим  передаточную функцию на элементарные дроби.  Для дальнейших упрощений  возьмем вместо  H(z)  выражение

.

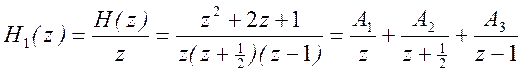Найдем константы разложения  (вычеты)

,

,

.

.

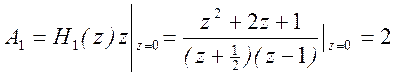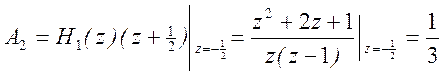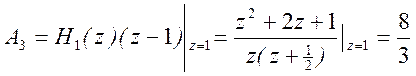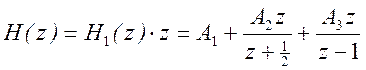Найдем импульсную характеристику как от суммы элементарных дробей

.

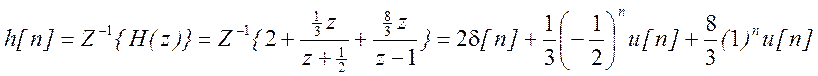Сигнал  является собственной функцией линейной дискретной системы. Поэтому  выходной сигнал при данном входе  есть .

Запишем  системы при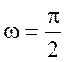

.

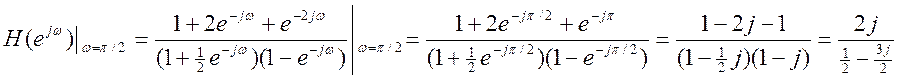Поэтому

.

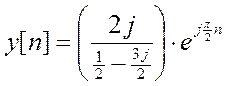9.  Найдите частотные характеристики системы с уравнением   и её реакцию на вход  

в установившемся режиме.

Решение.

Z- преобразование от уравнения при нулевых начальных условиях

,

передаточная функция системы    .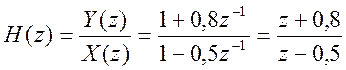

Частотная характеристика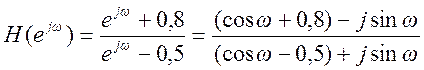  

Квадрат  АЧХ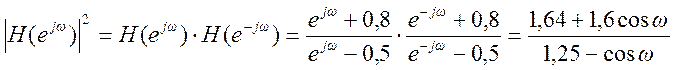    

АЧХ  системы ,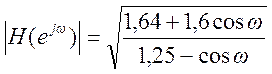

 ФЧХ  .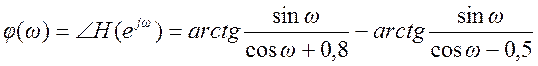

В установившемся режиме выходной сигнал ЛДС при входном сигнале   есть 

.

Определим значения АЧХ и ФЧХ для

 

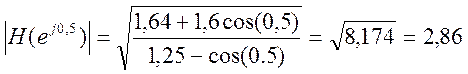
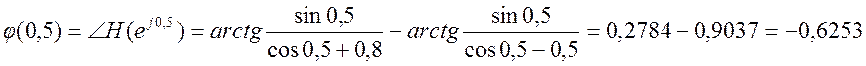
Выходной сигнал в установившемся режиме для