НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Расчетно-графическая работа по курсу
«Теория и обработка сигналов»
5 - й семестр
Вариант – 8,9.
Студент=[Введите студента] Преподаватель:
Факультет: АВТ [Введите препода]
Группа=[Введите группу]
Новосибирск
2006
1.8. Определите, является ли
периодическим сигнал ![]() и найдите его период.
и найдите его период.
Ответ. Периодический
сигнал с периодом ![]() .
.
Сигнал является периодическим, если x(t)=x(t+T). Проверим это для заданной функции:
x(t+T)=[cos(1-2(t+T)+1]2=[cos(1-2t-2T)+1]2
Так как cos – это периодическая функция с периодом π, то данная функция так же является периодической с Т= π.
1.9. Является ли
линейной и инвариантной во времени система с уравнением ![]() ?
?
Ответ.
Система – линейная, неинвариантная во времени.
Система является линейной, если она удовлетворяет принципу суперпозиции. То есть, если
![]() ,
то
,
то 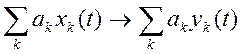
Проверим это для данной системы:
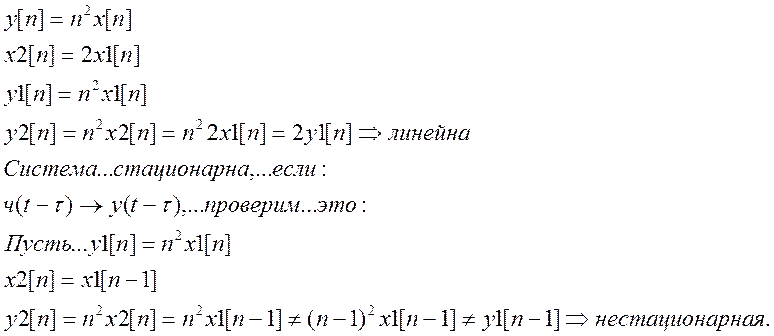
2.8. Разложите в ряд Фурье
сигнал
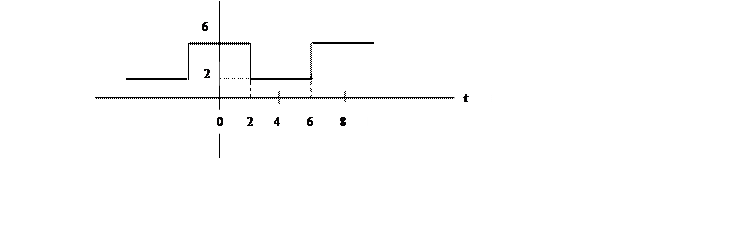
и постройте его амплитудный спектр.
Ответ. 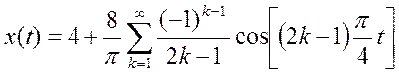
Т=8, w0=
![]()
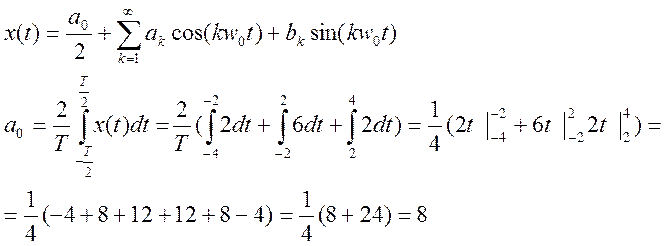
Так как функция четная, то ![]() =0. Найдем
=0. Найдем ![]() :
:
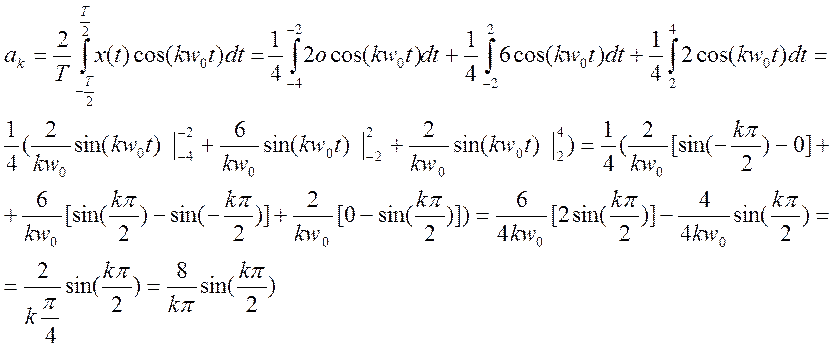
При всех четных k коэффициент обращается в 0,а при нечетных равен либо 1, либо -1, поэтому его можно заменить эквивалентным выражением:
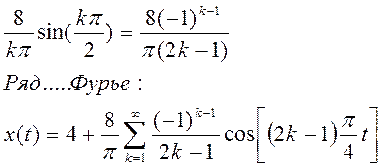
![]()
![]()
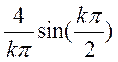
Так как мнимая часть отсутствует, то амплитудный спектр будет описывать сама функция.
Его амплитудный спектр (без постоянной = 4):
k=-15:0.1:15;
x=4./(k*pi);
y=x.*sin(k*pi./2);
plot(k,y);
title('Amplitude');
xlabel('k');
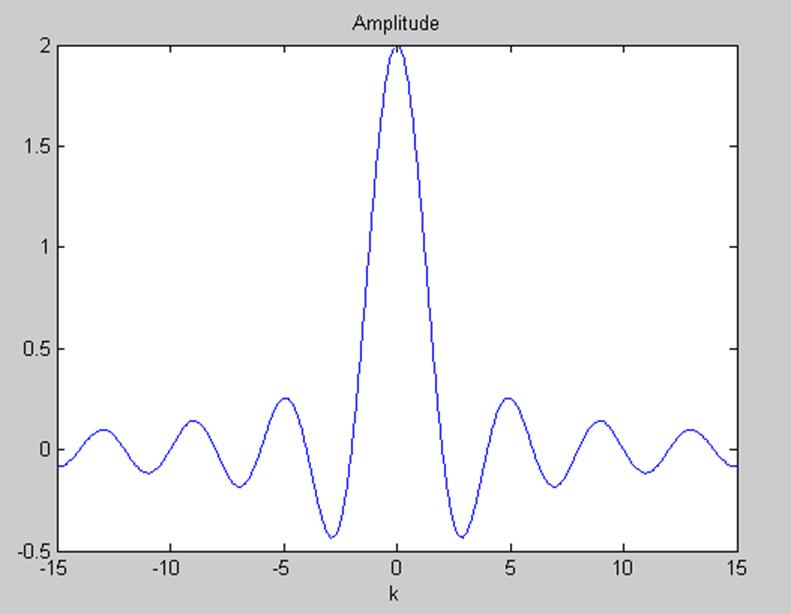 |
2.9.
Определите амплитудный и фазовый спектры периодического сигнала и постройте их
графики

Ответ. 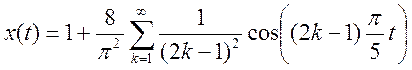
Т=10
w0=π/5
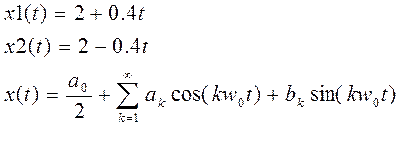
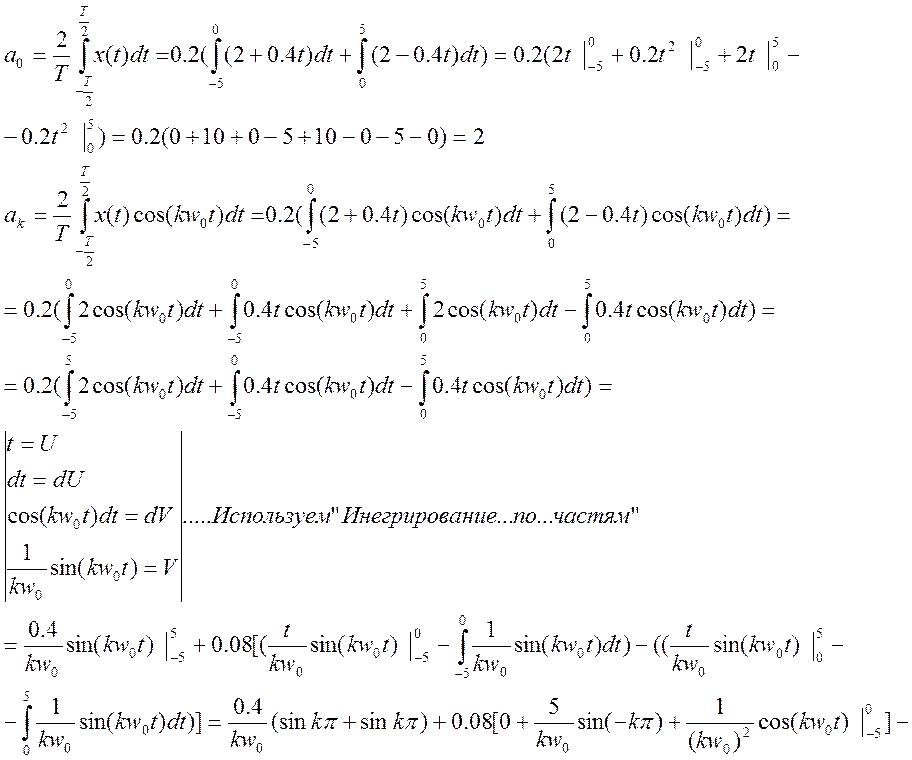
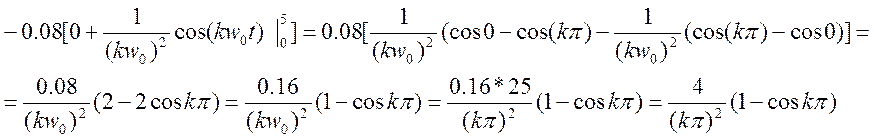
Видно, что при четных k коэффициент обращается в 0, а при нечетных – в 2. Поэтому его можно упростить:
![]()
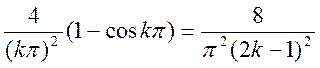
Так как функция четная, то второй коэффициент, как и в первом случае равен 0.
Ряд Фурье :
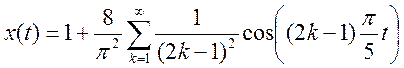
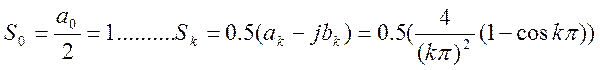
Построим амплитудный спектр:
k=-15:0.1:15;
x=2./(k*pi).^2;
y=x.*(1-cos(k*pi));
plot(k,y);
title('Amplitude');
xlabel('k');
 |
Так как ![]() -
действительное значение, то фазовый спектр является величиной постоянной и он равен
0.
-
действительное значение, то фазовый спектр является величиной постоянной и он равен
0.
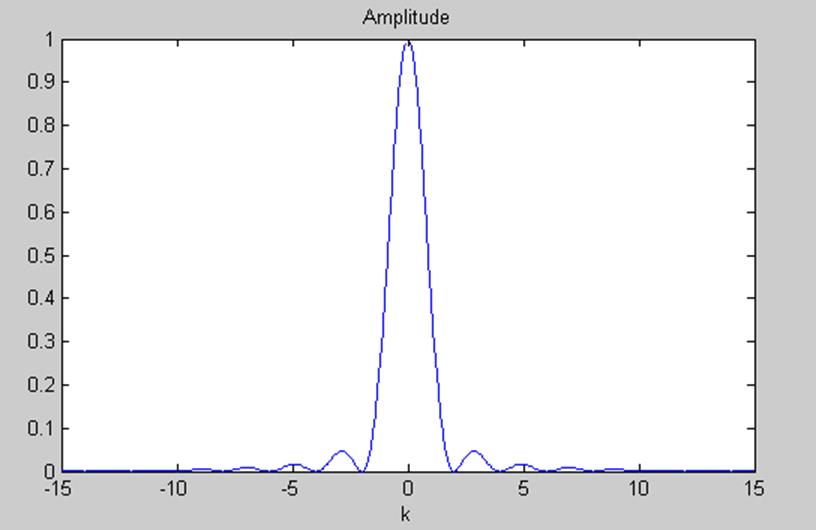
3.8. Найдите преобразование Фурье и постройте приближенный вид графика амплитудного спектра следующего сигнала
![]() ,
где u(t)
- единичная ступенчатая функция.
,
где u(t)
- единичная ступенчатая функция.
Ответ: 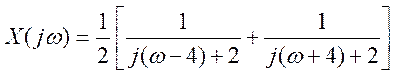 .
.
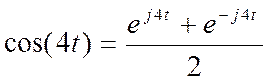
Поэтому можно сначала найти ПФ
для ![]() , а затем использовать свойство временного
сдвига ПФ.
, а затем использовать свойство временного
сдвига ПФ.
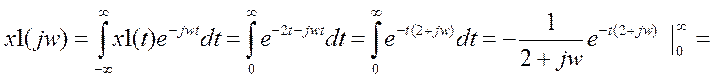
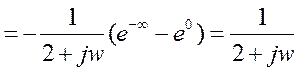
Теперь используем свойство сдвига. ПФ заданного сигнала будет состоять из 2-х слагаемых, так как cos равен половине суммы двух экспонент. В первом слагаемом это будет сдвиг w на 4, а во втором на -4. Для заданного сигнала ПФ будет иметь вид:
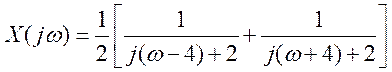
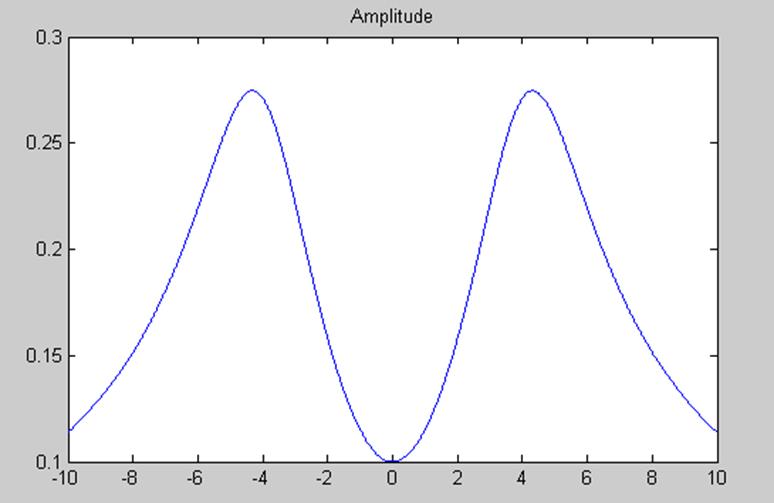
w=-10:0.01:10;
f=0.5./(2+j*w+j*4);
y=f +0.5./(2+j*w-j*4)
plot(w,abs(y));
title('Amplitude');
 |
3.9. Найдите вид сигнала во временной области, если преобразование Фурье сигнала имеет вид
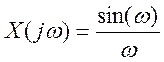 .
.
Ответ. 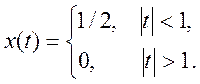
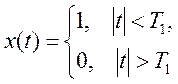 соответствует ПФ=
соответствует ПФ= 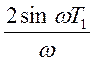 , поэтому x(t) для заданного ПФ
, поэтому x(t) для заданного ПФ
Будет иметь вид: 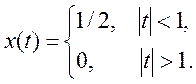 , так как Т1=1, и в ПФ присутствует
коэффициент, равный 2.
, так как Т1=1, и в ПФ присутствует
коэффициент, равный 2.
4.8.
Определите ДПФ сигнала 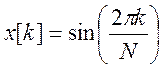 ,
для N = 8.
,
для N = 8.
Ответ: X[k] = {0 -j4 0 0 0 0 0 j4}
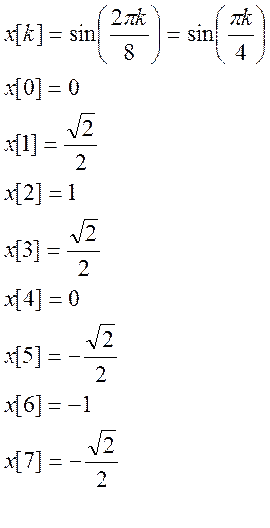
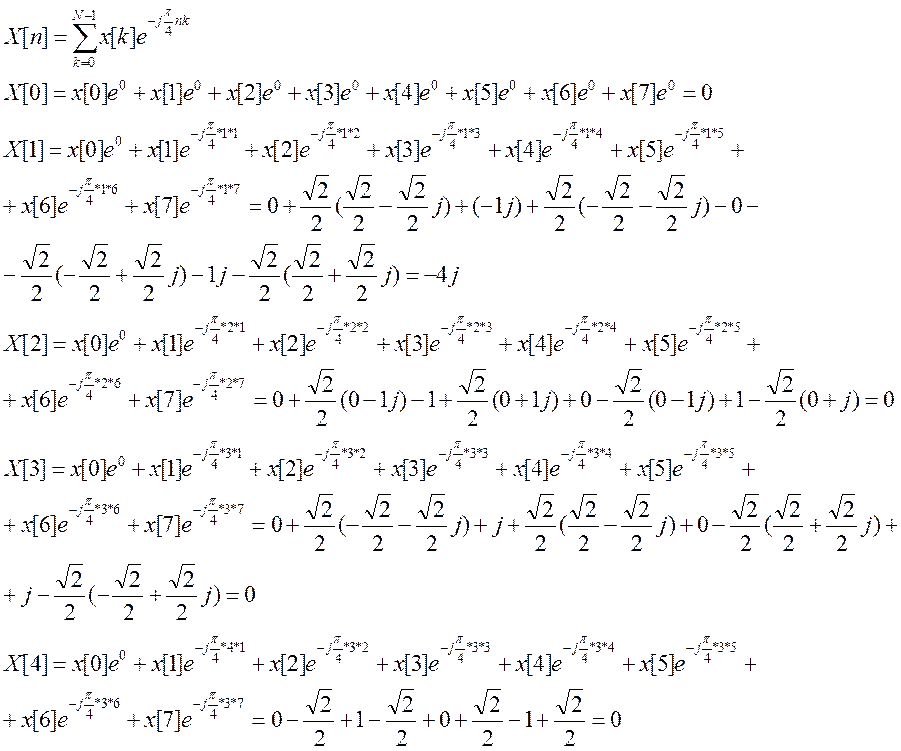
Остальные значения можно определить, используя свойство сопряженности.
Например, на месте 5-ом будет стоять комплексное сопряжение для 8-5=3-его места, на 6-ом – комплексное сопряжение для 2-го, на 7-ом, комплексное сопряжение для 1-го.
ДПФ имеет вид:
X(jw)={0,-4j,0,0,0,0,0,4j}
4.9.
Вычислите ДВПФ и ДПФ сигнала ![]() .
.
Ответ. ![]() ,
, ![]()
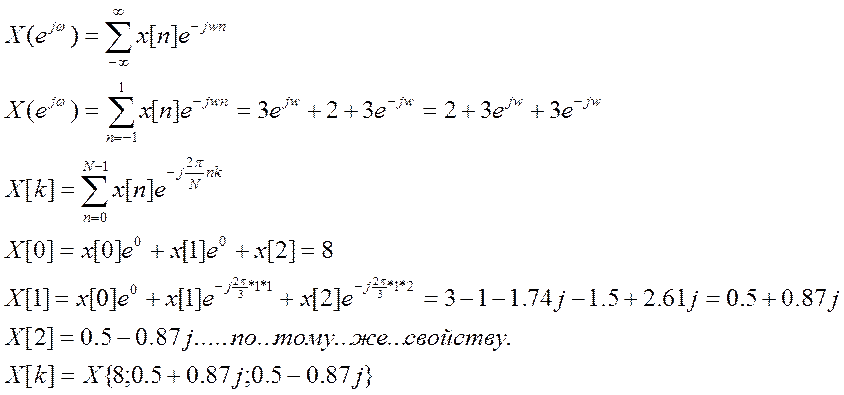
5.8. Вычислите дискретную
свертку двух сигналов, изобразите график свертки
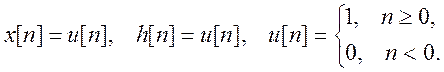
Ответ. ![]()
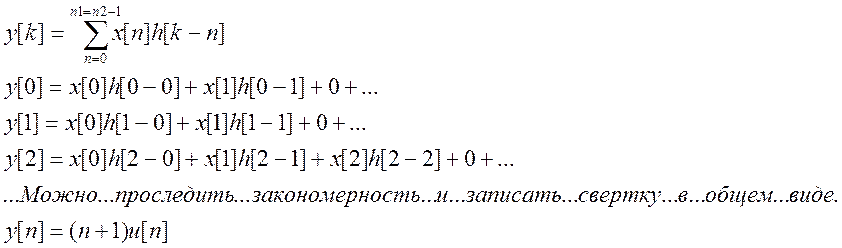
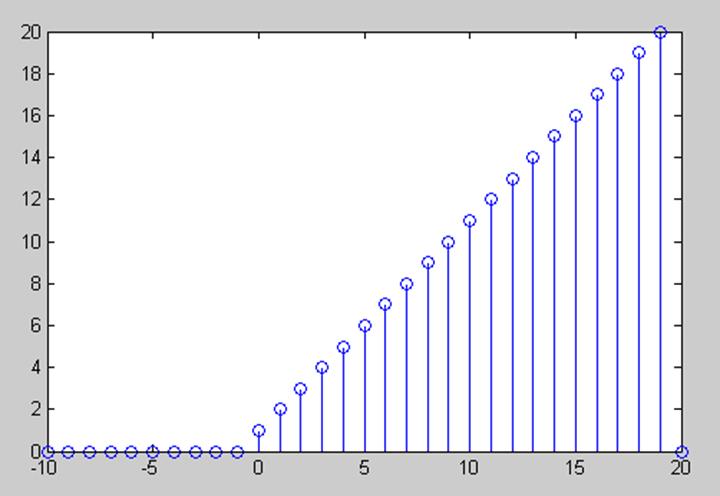 |
5.9. Вычислите свертку двух
непрерывных сигналов и изобразите её график
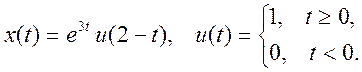
![]() .
.
Ответ. 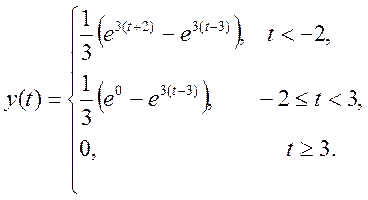
t=-10:0.01:2;
x=exp(3*t);
subplot(211);
plot(t,x);
title('x(t)');
T=-5:0.01:5;
h=rectpuls(T-0.5,5);
subplot(212);
plot(T,h);
title('h(t)');
xlabel('time');
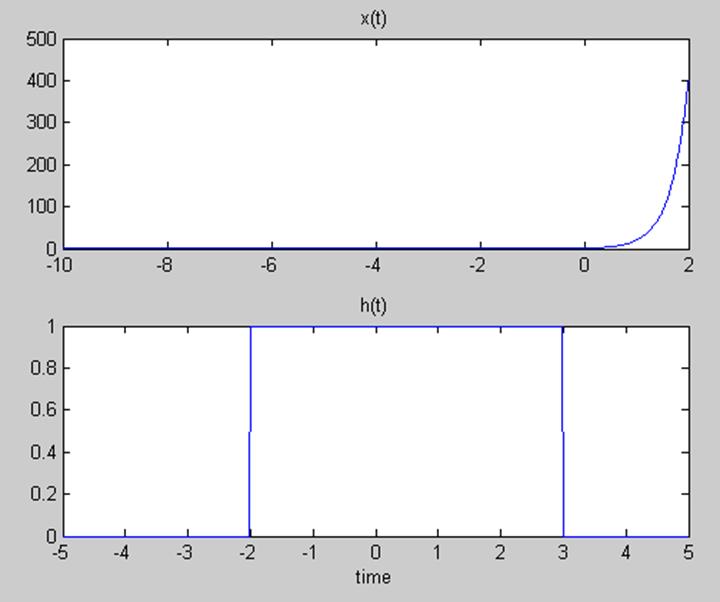 |
В данном случае лучше взять x(t-τ). Получим выражение для свертки:
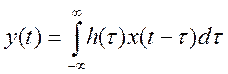
После «зеркального отображения» сигнала x(t), то есть x(-t), а так же его сдвиге на t=3, пересечение с сигналом h(t) будет равно нулю. Поэтому для всех t>3, y(t)=0. Для t, лежащего в интервале от -2 до 3, свертку необходимо искать в таком виде :
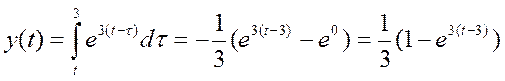
Если же t<= -2 то свертку надо искать так:
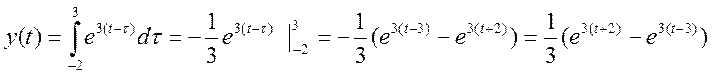
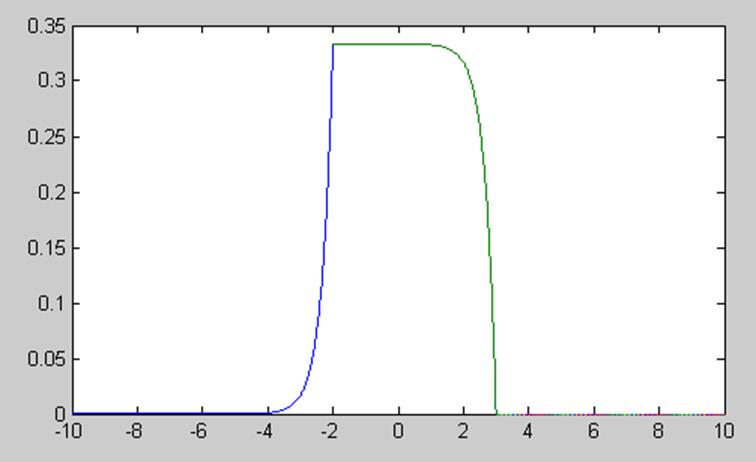
График свертки:
t1=-10:0.01:-2;
f1=(1./3).*(exp(3*t1+6)-exp(3*t1-9));
t2=-2:0.01:3;
f2=(1./3).*(1-exp(3*t2-9));
t3=3:0.01:10;
f3=0;
plot(t1,f1,t2,f2,t3,f3);
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.