Задачи 1
Лекционный материал - лекции № 1и № 2.
1.Какой
характер поведения имеет сигнал ![]() при комплексных
значениях С и a?
при комплексных
значениях С и a?
Решение.
Пусть C и a – комплексные. Выразим их как ![]() и
и
![]() . При этом
. При этом
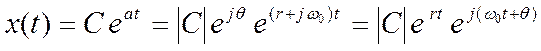 .
.
Используя формулу Эйлера ![]() , функцию x(t) можно выразить в виде
, функцию x(t) можно выразить в виде
![]() .
.
Для r
= 0 получаем комплексный периодический сигнал с периодом 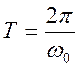 , действительная и мнимая части
которого – гармоники с частотой
, действительная и мнимая части
которого – гармоники с частотой ![]()
![]() .
.
Для r < 0 имеем комплексный периодический сигнал, умноженный на затухающую экспоненту. Действительная и мнимая часть такого сигнала – затухающие гармоники.
График поведения действительной
части для ![]()
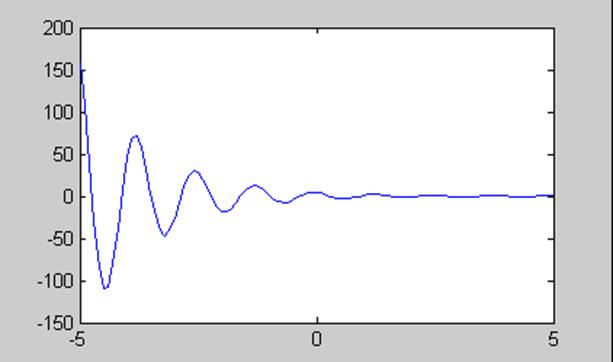
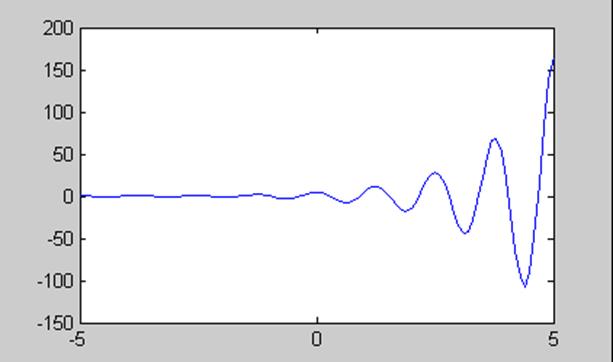
При ![]() получаем
периодический комплексный сигнал, действительная и мнимая части которого
гармоники с возрастающей амплитудой
получаем
периодический комплексный сигнал, действительная и мнимая части которого
гармоники с возрастающей амплитудой
![]()
График действительной части для ![]()
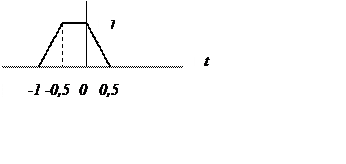
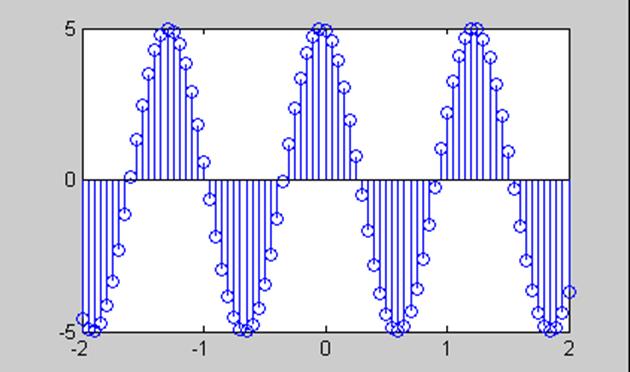
2. На рис. приведен сигнал x(t).
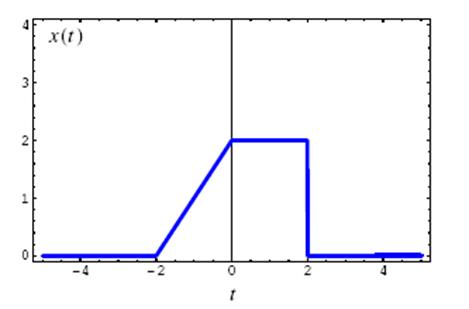
Построить графики сигналов
а) x(-t),
б) x(2t),
в)x(t-2), г)x(t+2).
|
а) б)
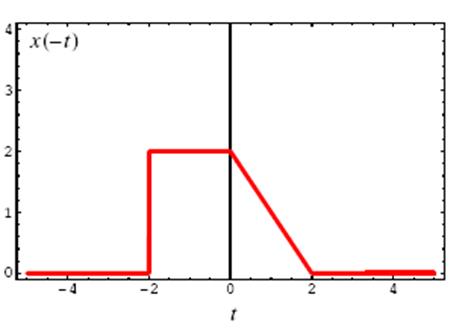
в) г)
|
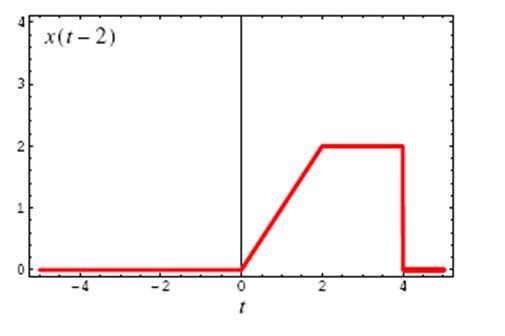
3. Пусть сигнал x(t) имеет вид
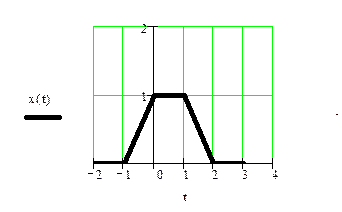
Найти x(2t+1).
Решение. Преобразование x(2t+1) – совокупность двух операций над x(t): временной сдвиг влево на 1 и сжатие по времени с коэффициентом 2.
Результат
4. 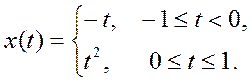 Сигнал
x(t) имеет вид
Сигнал
x(t) имеет вид
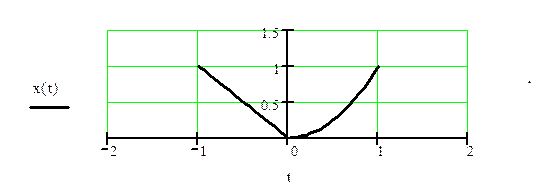
Определить четную и нечетную составляющие сигнала.
Решение.
Для получения x(-t) реверсируем x(t) по аргументу t.
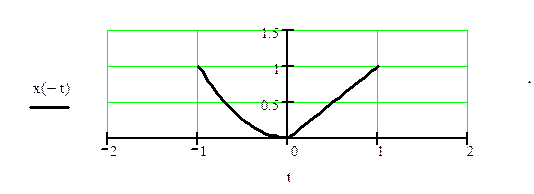
Четная составляющая сигнала
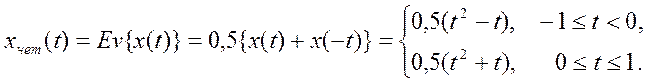
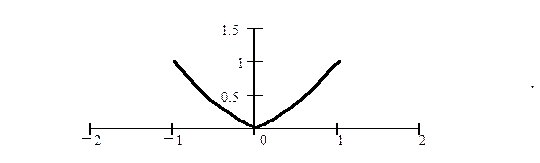
Нечетная составляющая
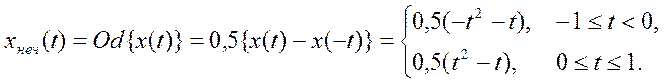
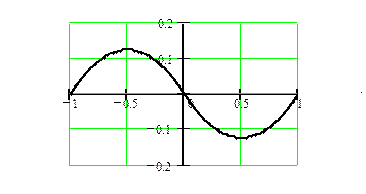
5. Сигнал
![]() , Определить период x(t).
, Определить период x(t).
Решение.
Сумма
двух периодических сигналов ![]() , где x1(t) и x2(t) –периодические
сигналы с периодами T1 и Т2
соответственно, является также периодическим сигналом с периодом, равным
наименьшему общему кратному T1
и Т2. Пусть
, где x1(t) и x2(t) –периодические
сигналы с периодами T1 и Т2
соответственно, является также периодическим сигналом с периодом, равным
наименьшему общему кратному T1
и Т2. Пусть 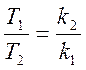 , положим
, положим ![]() . Для периодического сигнала
. Для периодического сигнала
![]() .
.
Для сигнала cos(3t) ![]() , для сигнала sin(5t)
, для сигнала sin(5t) ![]() ,
, 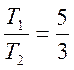 .
Поэтому период их суммы
.
Поэтому период их суммы ![]()
6. Дискретный во времени сигнал имеет вид
![]() .
Определить период x[n].
.
Определить период x[n].
Решение.
Если x[n] – периодический с периодом N сигнал, то
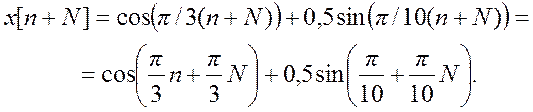
По условию периодичности x[n]
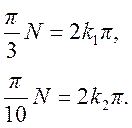 Или
Или 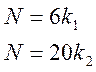
Наименьшее N, удовлетворяющее этим условиям, - это наименьшее общее кратное чисел 6 и 20, следовательно, период N = 60.
7.
При каком условии гармоника дискретного времени ![]() является периодическим сигналом?
является периодическим сигналом?
Решение.
Гармоника непрерывного времени ![]() - периодическая с
периодом
- периодическая с
периодом ![]() .
.
Гармоника дискретного времени ![]()
периодическая, если имеется такое N
> 0, что ![]() , т.е.
, т.е. ![]() . Следовательно, должно выполняться
условие
. Следовательно, должно выполняться
условие
![]() , где m,
N - положительные целые числа. Основная
угловая частота должна быть равна
, где m,
N - положительные целые числа. Основная
угловая частота должна быть равна 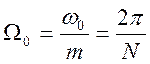 .
.
8. Уравнение
системы ![]() . Является ли эта система
. Является ли эта система
а) стационарной (инвариантной во времени)?
б) линейной?
в) физически осуществимой (каузальной)?
г) устойчивой?
Решение.
а) Положим ![]() . Тогда
. Тогда ![]() .
Следовательно, система стационарная.
.
Следовательно, система стационарная.
б) Для ответа на вопрос о
линейности системы положим ![]() . При этом x2(t)=2x1(t), но y2(t)≠2y1(t), что
должно быть для линейной системы, значит, система – нелинейная.
. При этом x2(t)=2x1(t), но y2(t)≠2y1(t), что
должно быть для линейной системы, значит, система – нелинейная.
в) Система является каузальной, поскольку выходной сигнал y(t0) в момент t0 зависит только от сигнала при t0 и не зависит от будущих значений сигнала.
г) Чтобы ответить на
вопрос об устойчивости системы, возьмем ограниченный входной сигнал ![]() , тогда
, тогда ![]() .
Следовательно, система - устойчивая.
.
Следовательно, система - устойчивая.
9. .
Пусть система дискретного времени описывается уравнением:
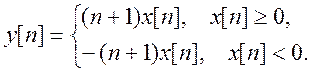
Является ли эта система
а) стационарной (инвариантной во времени)?
б) линейной?
в) устойчивой?
Решение.
а) Пусть ![]() . Тогда выходной сигнал системы
. Тогда выходной сигнал системы 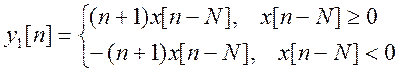 .
.
Для стационарной (инвариантной во времени) системы должно выполняться условие
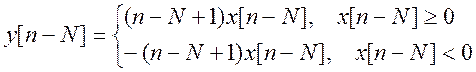 .
.
Так как ![]() ,
то система нестационарная.
,
то система нестационарная.
б) Линейная система должна удовлетворять принципу суперпозиции.
Для входного сигнала ![]() выходной сигнал
выходной сигнал 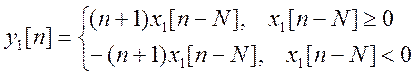 .
.
Аналогично для ![]()
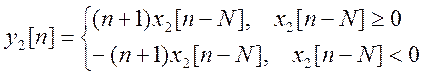 .
.
Линейной комбинации этих
сигналов ![]() соответствует выход системы
соответствует выход системы
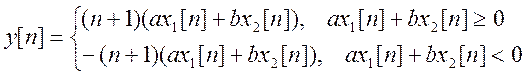 .
.
Для линейной системы выход должен удовлетворять условию
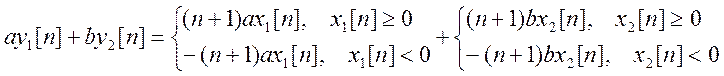 .
.
Поскольку ![]() , то система нелинейная.
, то система нелинейная.
в) Для устойчивой системы
ограниченному входному сигналу должен соответствовать ограниченный выходной
сигнал. Для данной системы ![]() соответствует
неограниченный выход. Значит, система – неустойчивая.
соответствует
неограниченный выход. Значит, система – неустойчивая.
Задачи для самостоятельного решения

Найдите x(3t-2).
Ответ.
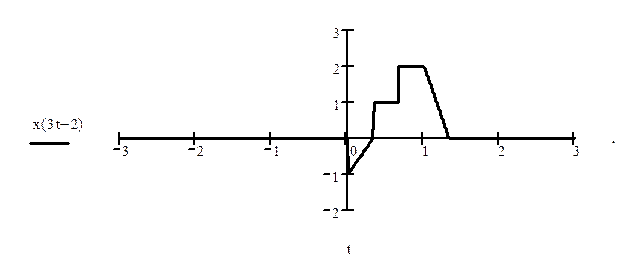
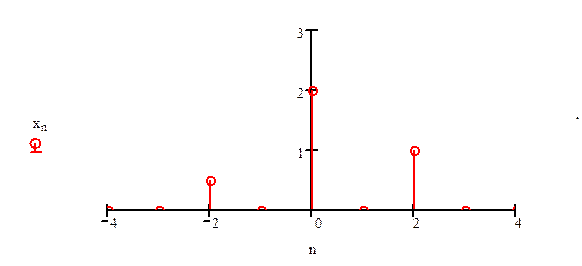
Найдите x[4-2n].
Ответ.
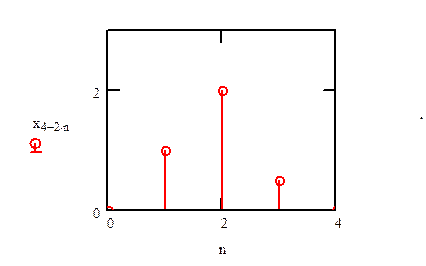
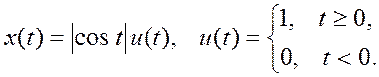
Ответ.
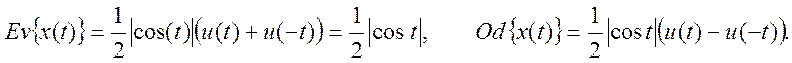
4. Пусть
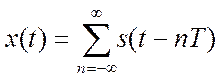
периодический с периодом Т непрерывный во времени сигнал. Изобразите графики сигнала для
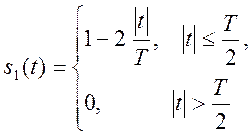
и
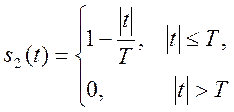
5. Найдите период сигнала
![]()
Ответ. Период T = π.
6. Исследуйте характер
поведения экспоненциального сигнала дискретного времени ![]() при комплексных значениях
при комплексных значениях ![]() .
.
7. Определите, является
ли периодическим сигнал ![]() и найдите его
период.
и найдите его
период.
Ответ.
Периодический сигнал с периодом ![]() .
.
8. Является ли линейной
и инвариантной во времени система с уравнением ![]() ?
?
Ответ.
Система – линейная, неинвариантная во времени.
10. Определите, является
ли линейной, стационарной (инвариантной во времени) и устойчивой система-
интегратор с уравнением 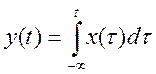 ?
?
Ответ. Система - линейная, инвариантная во времени, но неустойчивая.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.