2.4. Периодические сигналы.
2.4.1. Ряд Фурье
.
Сигнал s(t) называется периодическим, если он точно повторяет свои значения через одинаковые интервалы времени , т.е.
![]() , (2.37)
, (2.37)
где n = 0, 1, 2, ...
При этом наименьший интервал повторения Т называется периодом, а частота повторения f0 =1/T называется основной частотой. В строгом смысле периодический сигнал физически неосуществим, так как реальный сигнал не может продолжаться вечно. Поэтому периодический сигнал - это полезная математическая модель.
Любой конечный периодический с периодом Т сигнал можно разложить в ряд Фурье вида
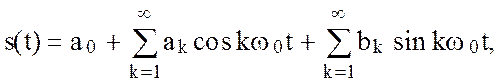 (2.38)
(2.38)
где 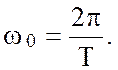
Коэффициенты этого ряда
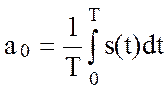 (2.39)
(2.39)
и
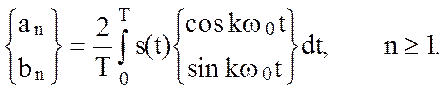 (2.40)
(2.40)
Эта форма ряда называется тригонометрической. Она представляет собой частный случай обобщенного ряда Фурье по конкретной тригонометрической системе ортогональных функций 1, cosw0t, sinw0t, cos2w0t, sin2w0t, ...
В выражениях (2.39), (2.40) в качестве интервала интегрирования может
использоваться любой интервал длиной Т, в частности 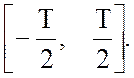 Отсюда очевидно следует, что для
четной функции s(t) = s(-t) все коэффициенты bk
= 0 и соответствующий ряд Фурье не содержит синусов
Отсюда очевидно следует, что для
четной функции s(t) = s(-t) все коэффициенты bk
= 0 и соответствующий ряд Фурье не содержит синусов
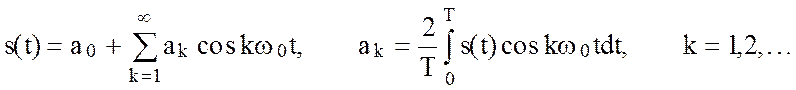 (2.41)
(2.41)
Для нечетной функции s(t) = -s(t) все коэффициенты ak = 0 и соответствующий ряд Фурье не содержит косинусов
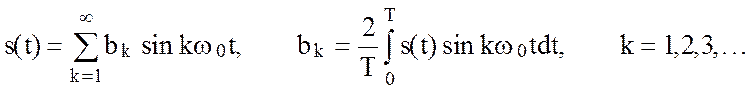 (2.42)
(2.42)
В математическом анализе [7],[9] доказывается, что если периодическая функция s(t) удовлетворяет условиям Дирихле, то ее ряд Фурье сходится к самой функции в точках непрерывности функции и к полусумме
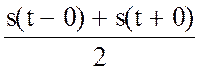
в точках
разрыва. Для непрерывной функции ее коэффициенты Фурье убывают со скоростью ![]() , а, если s(t) имеет
конечные разрывы, то со скоростью
, а, если s(t) имеет
конечные разрывы, то со скоростью ![]()
Тригонометрический ряд Фурье можно записать также в виде
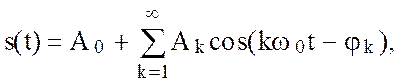 (2.43)
(2.43)
где
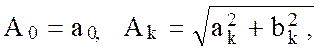
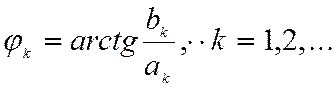 (2.44)
(2.44)
Переход от Ak к ak и bk осуществляется по формулам
![]() (2.45)
(2.45)
Ряд Фурье функции s(t) можно представить и в комплексной (экспоненциальной) форме
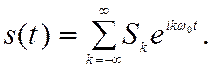 (2.46)
(2.46)
Коэффициенты этого ряда
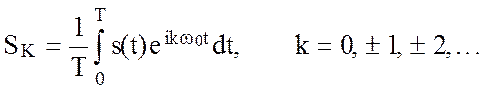 (2.47)
(2.47)
Выражения, связывающие коэффициенты комплексной и тригонометрической форм ряда Фурье, имеют вид
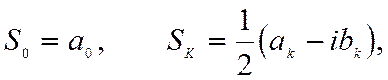 (2.48)
(2.48)
![]() . (2.49)
. (2.49)
Комплексная форма представляет собой частный случай обобщенного ряда, когда в качестве базиса разложения используется ортогональная система комплексных экспонент exp{ikw0t}, где k = 0, ±1, ±2, ... Комплексная форма более удобна для аналитических преобразований.
|
|
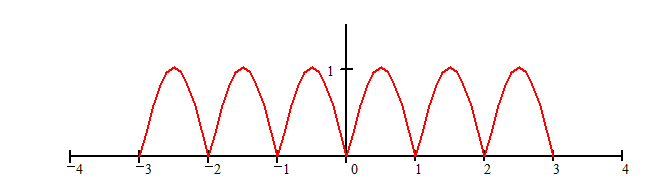
Пример. Разложим в ряд Фурье “выпрямленное” синусоидальное напряжение u(t) = Usinpt, 0 £ t £ 1 (рис. 2.2).
|
Рис.2.2.Вид “выпрямленного” синусоидального напряжения
Данная функция четная, поэтому все коэффициенты bk =0. В интервале [0, 1] функция определяется формулой u(t) = Usinpt, при этом Т = 1, w0 = 2p. Найдем коэффициенты ak
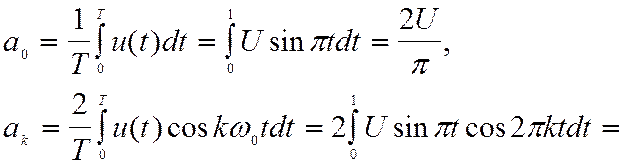
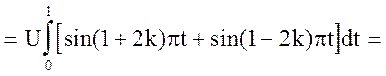
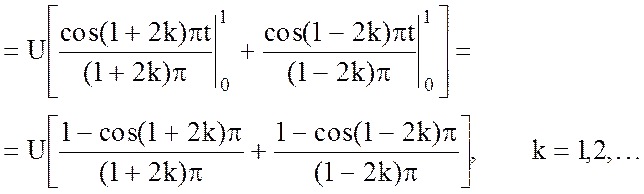
Для всех k ¹
0, cos(1±2k)p = -1 и 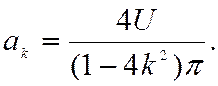
Таким образом, ряд Фурье для рассматриваемого примера имеет вид
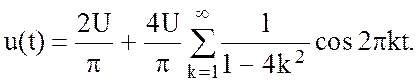
2.4.2. Спектры периодических сигналов.
В теории сигналов широкое применение получило понятие спектра сигнала, имеющего смысл, связанный с разложением сигнала на частотные составляющие. Основой спектрального разложения периодического сигнала является представление его в виде ряда Фурье:
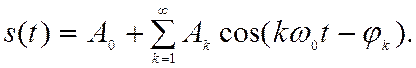 (2.50)
(2.50)
Оно показывает, что периодический сигнал с периодом Т
имеет частотные (спектральные) составляющие с угловыми частотами 0, w0, 2w0, ..., nw0, ..., где 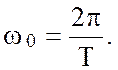
Совокупность величин Ak = Ak(kw0) образует амплитудный частотный спектр сигнала, а совокупность jk = jk(kw0) - фазовый частотныйспектр. Каждая отдельная компонента спектра называется гармоникой с соответствующим номером в виде
![]()
Комплексной гармонике
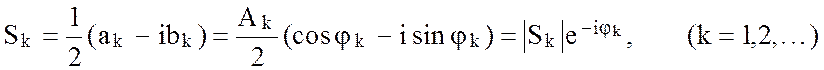
можно придать следующий смысл в комплексной плоскости.
Величина 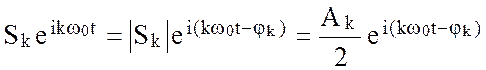 определяет в этой
плоскости вектор, имеющий длину
определяет в этой
плоскости вектор, имеющий длину 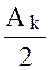 и составляющий
угол
и составляющий
угол ![]() с положительной вещественной осью
(рис.2.3).
с положительной вещественной осью
(рис.2.3).
Конец этого
вектора при возрастании времени t описывает окружность радиуса ½Sk½ , при положительном k
вектор вращается в положительном направлении против часовой стрелки с угловой
скоростью wk = kw0, а при отрицательном k
- по часовой стрелке с той же угловой скоростью, гармоника ![]() получается сложением этих векторов.
получается сложением этих векторов.
|
|
![]()
![]()

![]()
![]()
 Рис. 2.3. Представление комплексной гармоники
Рис. 2.3. Представление комплексной гармоники
Спектр имеет составляющие только на частотах 0, w0, 2w0, ..., kw0, ... или 0, ±w0, ±2w0, ..., ±kw0, поэтому он является линейчатым (не сплошным).
Пример графического представления спектра амплитуд и спектра фаз периодического сигнала показан на рис.2.4.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.