Периодические и непериодические сигналы, страница 4

Обозначим через   dS = S(f)df.  Тогда

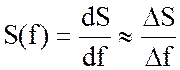
                                                                                 (2.70)

Следовательно,  S(f)  имеет смысл плотности амплитуды гармоник, приходящихся на единичный интервал частоты вблизи рассматриваемой частоты  f. Этим и объясняется название   S(f) - спектральная плотность.

В общем случае  S(f)  является комплексной функцией действительного аргумента   f. Ее можно представить в показательной форме.

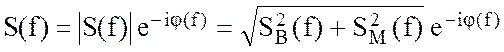            ,   где             (2.71)

           

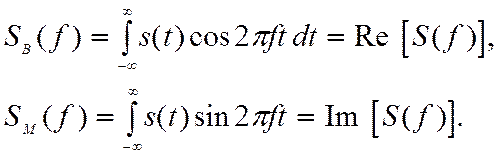
Зависимость  |S(f)|  называется амплитудным спектром непериодического сигнала. Он характеризует плотность амплитуды гармоник, входящих в непрерывный сигнал. Зависимость 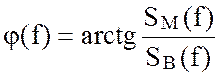   является фазовымспектром, отражающим зависимость от частоты начальных фаз гармоник сигнала.

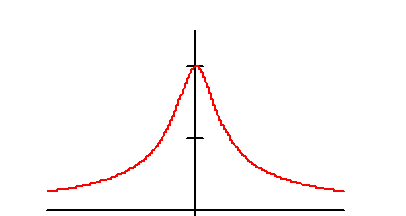
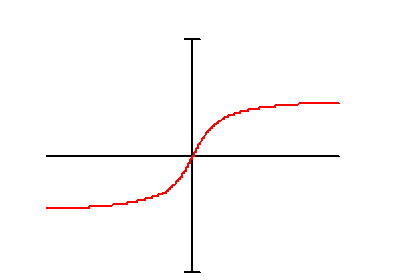
На рис. 2.10 представлены графики общего вида амплитудного и фазового спектра непериодического сигнала.

            Рис. 2.10. Амплитудный и фазовый спектры сигнала s(t)

В отличие от линейного спектра периодического сигнала спектры непериодических сигналов являются сплошными. При этом амплитудный спектр представляет четную функцию частоты, а фазовый  -  нечетную.

Поведение фазового спектра связано с амплитудным спектром функции. Большие изменения фазы происходят около нуля амплитудного спектра и наоборот, если амплитуда изменяется быстро, фазовый спектр меняется незначительно. Это видно  и  из рис.2.10.

2.5.3. Примеры  спектров  непериодических  сигналов.

2.5.3.1. Прямоугольный импульс.

Такой импульс единичной  амплитуды определяется выражением

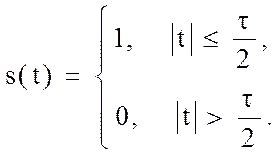                                                                                    (2.72)

Преобразование Фурье этой функции  s(t)   равно

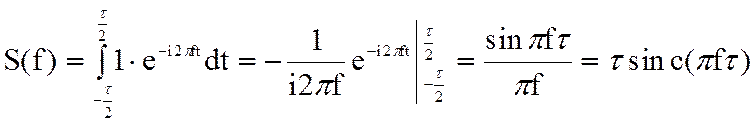            (2.73)

Так как функция s(t)   в этом случае четная, то преобразование Фурье  S(f) оказалось действительной функцией.

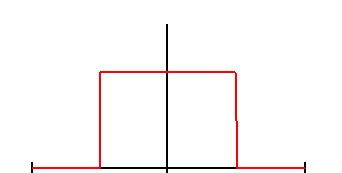
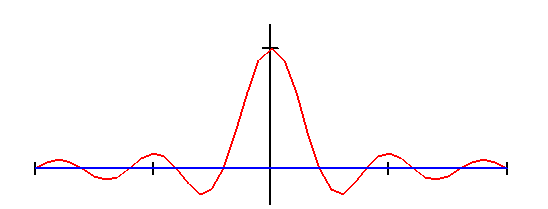
На рис. 2.12 изображены s(t) и  S(f)   для прямоугольного импульса.

s(t)    S(f)    f    0    t    0

            Рис. 2.12. Прямоугольный импульс и его преобразование Фурье

Из обратного преобразования Фурье следует

                       

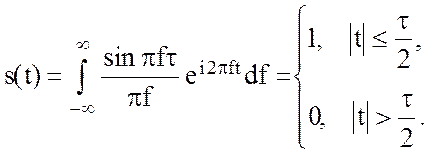
Если  же 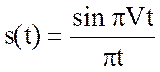, то для такой функции преобразование Фурье  имеет вид

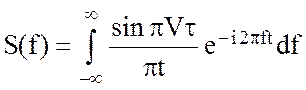                                                                                (2.74)

 Этот интеграл и предыдущий идентичны, если выполнить замену переменной t = - t¢ .Следовательно, преобразование Фурье для 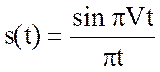 имеет вид

                                   

t

f

0

«

S(f)

s(t)

                                         

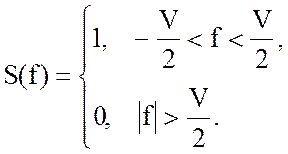
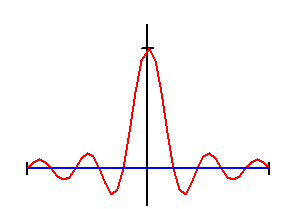
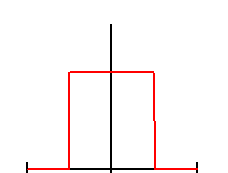
               Рис. 2.13.  Преобразование Фурье функции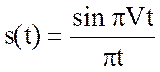 

Этот пример является иллюстрацией теоремы (свойства) двойственности преобразования Фурье, которое ниже будет подробно рассмотрено.

2.5.3.2. Треугольный импульс.

Для этого импульса

                                                                                          (2.75)

Преобразование Фурье для такого сигнала

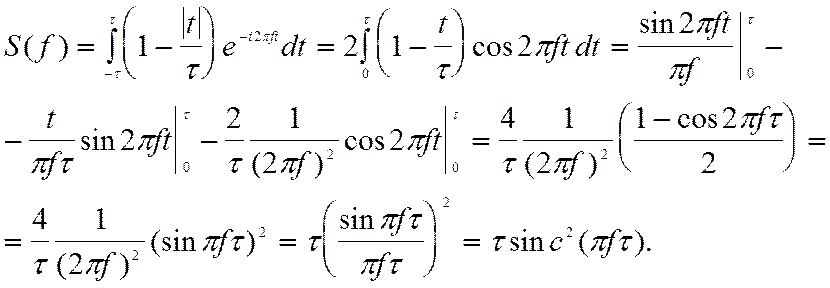(2.76)

1    0   -t    t    0    f    t    t       «

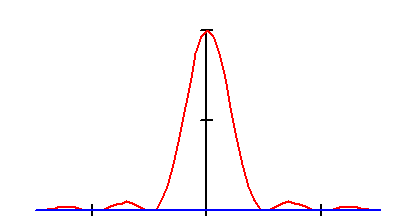
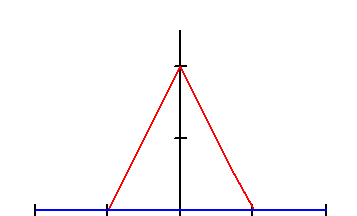
Рис. 2.14. Треугольный импульс и его преобразование Фурье

На рис. 2.14 показаны треугольный импульс и его преобразование Фурье (амплитудный  спектр).

Для треугольного импульса функция   S(f)  убывает пропорционально  1/f  ²  , а не  1/f  , как у прямоугольного, так как  S(f)   в этом случае -  непрерывная функция.

В примерах ,приведённых выше, рассмотрены вычисления спектров некоторых простых, часто используемых сигналов. Для других  реальных сигналов спектральный анализ может потребовать сложных вычислений. В этих. случаях для проведения вычислений и построения графиков могут оказаться полезными современные программные системы для автоматизации научно-технических вычислений, такие как MathCAD  фирмы Mathsoft,  MatLab   фирмы               MathWorks, Mathematica фирмы Wolfram Research  и др.[14].