|
|
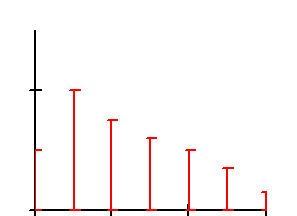
Рис. 2.4. Графическое представление амплитудного и фазового спектров
периодического сигнала
Напомним, что для непрерывного сигнала s(t) амплитуды
гармоник убывают со скоростью не менее 1/k2![]() , для сигнала, имеющего
разрывы 1-го рода, - со скоростью не менее
, для сигнала, имеющего
разрывы 1-го рода, - со скоростью не менее ![]()
Для комплексного ряда Фурье
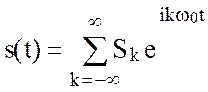 . (2.51)
. (2.51)
Комплексные гармоники Sk и S-k являются комплексно- сопряженными величинами.
Действительно,
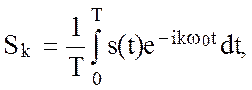 (2.52)
(2.52)
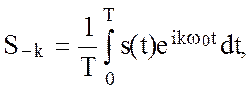 (2.52a)
(2.52a)
и, следовательно ![]()
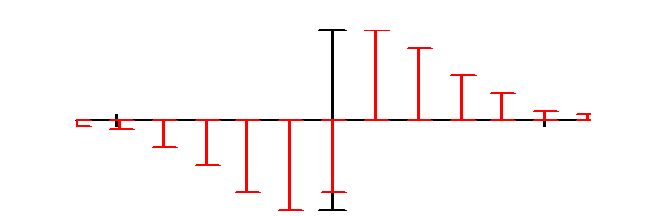
Из этого следует, что спектр амплитуд ½Sk½ - четная функция, а спектр фаз - нечетная функция. На рис. 2.5 дан пример графического представления спектра амплитуд и спектра фаз периодического сигнала для комплексной формы ряда Фурье.
Ввиду симметрии для действительного сигнала s(t) достаточно отображать только часть спектра, соответствующую положительным частотам.
|

|
Рис. 2.5. Графики амплитудного и фазового спектра для комплексной формы ряда Фурье
Другая возможная форма представления спектра при комплексной форме Фурье - использование действительной части Re[Sk] и мнимой части Im[Sk] для каждого комплексного значения Sk.
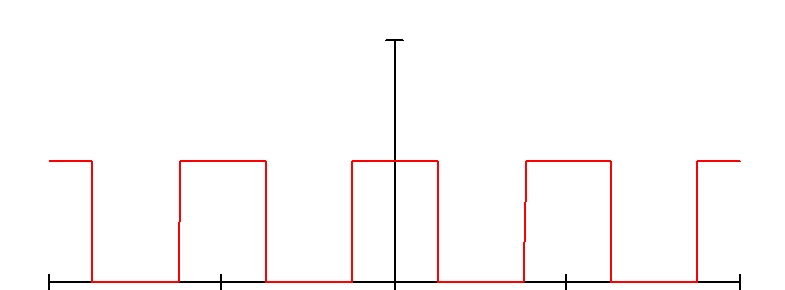
Пример. Рассмотрим спектр периодической последовательности прямоугольных импульсов (рис.2.6), которая широко используется в системах различного назначения.
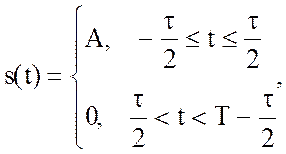
|
|
Рис. 2.6. Периодическая последовательность прямоугольных импульсов
Найдем коэффициенты Фурье данного сигнала:
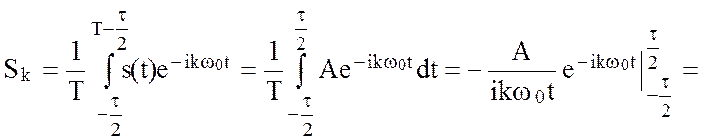
=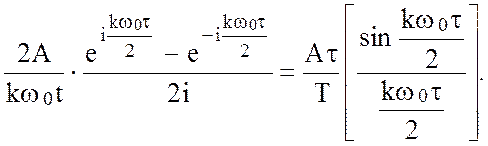 (2.53)
(2.53)
Функция в
квадратных скобках имеет вид 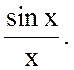 В теории сигналов
она играет важную роль, обозначается как sinc(x) = sin x/x и
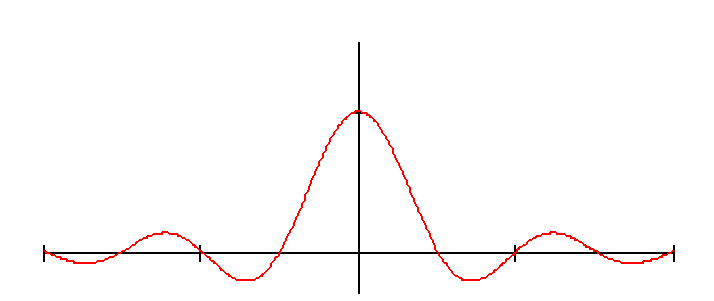
называется функцией отсчетов. Ее график показан на рис. 2.7. Функция
осциллирует с периодом 2p, спадая по
амплитуде с увеличением аргумента и переходя через 0 в точках x = ±p, ±2p, ±3p,
...
В теории сигналов
она играет важную роль, обозначается как sinc(x) = sin x/x и
называется функцией отсчетов. Ее график показан на рис. 2.7. Функция
осциллирует с периодом 2p, спадая по
амплитуде с увеличением аргумента и переходя через 0 в точках x = ±p, ±2p, ±3p,
...
|
|
Рис. 2.7. График функции sinc(x)
Запишем ряд Фурье рассматриваемого сигнала через функцию отсчетов. Так как
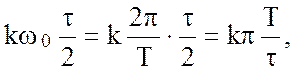 то
то 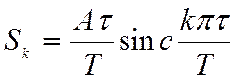 и
и
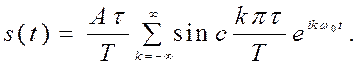 (2.54)
(2.54)
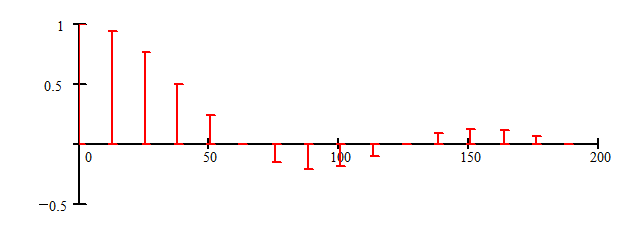
На рис. 2.8 изображены амплитудные спектры прямоугольной последовательности импульсов для двух случаев:
a) A = 1, T = 0,25 c, t = 0,05 c,
б) A = 1, T = 0,5 c, t = 0,05 c.
Видно, что с увеличением периода Т спектр становится более “частым”.
|
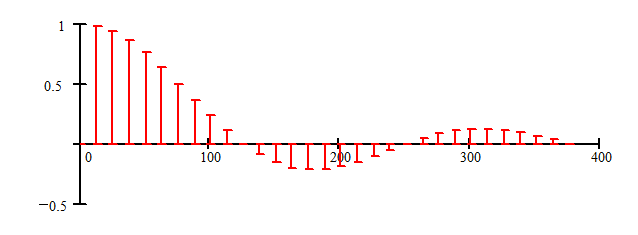
|
Рис. 2.8. Спектры прямоугольной последовательности импульсов
при различных значениях периода следования
2.4.3. Распределение мощности в спектре периодического сигнала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.